cho hàm số y=f(x)=\(\frac{2x^2-5x+3}{3x^2-x-1}\)
Tính khoảng cách giữa hai điểm cực trị của đồ thị hàm số đã cho.
giải giúp mình nha! mình tick cho!!! ^.^
Mọi người giúp mình với ạ!!! Mình cảm ơn rất nhiều!!!
1, Viết phương trình đường thẳng đi qua các điểm cực trị của đồ thị hàm số:
\(y=x^3-6x^2-3x+2\)
2, Cho hàm số: \(y=x^3-x^2+mx\)
Tìm m để đồ thị hàm số có các điểm cực đại, cực tiểu: A, B sao cho Δ OAB vuông góc tại O.
Cho hàm số y=3x^2 a) xác định tính đồng biến nghịch biến của hàm số b) Tính f(1); f(-1); f(2); (f(-4) có) Tìm x biết giá trị của hàm số bằng 48 d) vẽ đồ thị hàm số trên Giúp mình với nay KT giữa kì rồi:((
a: f(x)=3x^2
a=3>0
=>Hàm số đồng biến khi x>0 và nghịch biến khi x<0
b: f(1)=f(-1)=3*1^2=3
f(2)=3*2^2=12
f(-4)=3*(-4)^2=48
c: f(x)=48
=>x^2=48/3=16
=>x=4 hoặc x=-4
d; 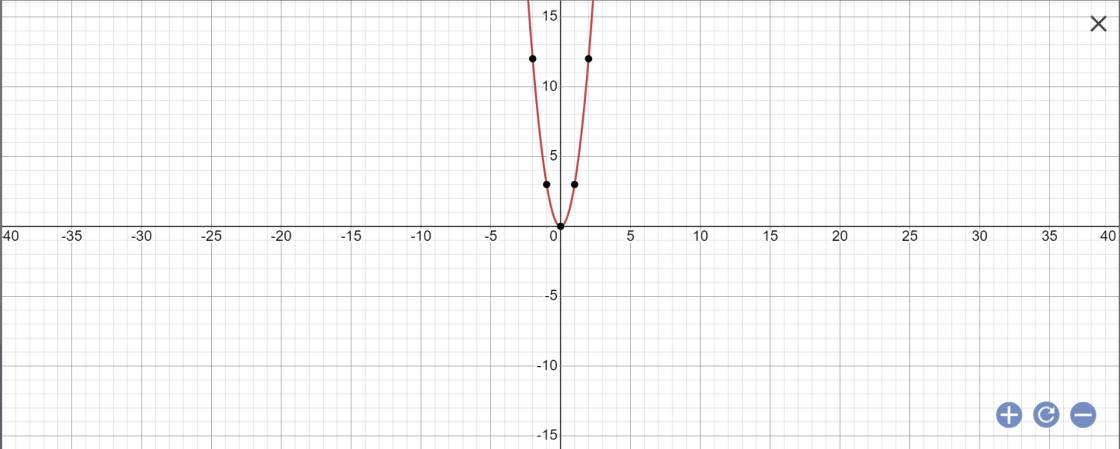
Cho hàm số y = f(x) = 2x và hàm số y = g(x) = - 3x. Xác định tọa độ điểm A trên đồ thị f(x) và tọa độ điểm B trên đồ thị g(x) biết chúng cùng có hoành độ bằng ( - 1). Tính diện tích tam giác OAB (với O là gốc toạ độ).
giúp mình gấp mình tick cho
Khoảng cách giữa hai điểm cực trị của đồ thị hàm số y = ( x + 1 ) ( x - 2 ) 2 bằng bao nhiêu?
A. 5 2
B. 2
C. 2 5
D. 4
Khoảng cách giữa hai điểm cực trị của đồ thị hàm số y = − x 3 + 3 x + 2 bằng
A. 3 5
B. 2 3
C. 2 5
D. 2
Đáp án C
Ta có y ' = − 3 x 2 + 3 ⇔ y ' = 0 ⇔ x = 1 x = − 1 ⇒ A 1 ; 4 B − 1 ; 0 ⇒ A B = 1 + 1 2 + 4 2 = 2 5
Bài 1: Cho hàm số y = f(x) = 2x và y = yx = 18/x. Không vẽ đồ thị của chúng, hãy tính tọa độ giao điểm của hai đồ thị
Bài 2: Cho hàm số y = -1/3 x
a, Vẽ đồ thị của hàm số
b, Trong các điểm M(1;3), N (6;2), P(9;-3). Điểm nào thuộc đồ thị hàm số
Mình cần gấp lắm ạ, mong mọi người giúp đỡ
Khoảng cách giữa hai điểm cực trị của đồ thị hàm số y = - x 3 + 3 x + 1
A. 2 5
B. 20
C. 6
D. 6
a) Cho \(y=2x^4+2mx^2-\dfrac{3m}{2}\). Tìm m để đồ thị hàm số có 3 điểm cực trị cùng với điểm O tạo thành 1 tứ giác nội tiếp.
b) Cho \(y=-2x^4-2mx^2+\dfrac{3m}{2}\). Tìm m để đồ thị hàm số có khoảng cách giữa 2 điểm cực đại bằng 5.
a. Hàm có 3 cực trị \(\Rightarrow m< 0\)
\(y'=8x^3+4mx=4x\left(2x^2+m\right)=0\Rightarrow\left[{}\begin{matrix}x=0;y=-\dfrac{3m}{2}\\x=-\sqrt{-\dfrac{m}{2}};y=-\dfrac{m^2+3m}{2}\\x=\sqrt{-\dfrac{m}{2}};y=-\dfrac{m^2+3m}{2}\end{matrix}\right.\)
Trong đó \(A\left(0;-\dfrac{3m}{2}\right)\) là cực đại và B, C là 2 cực tiêu
Do tam giác ABC luôn cân tại A \(\Rightarrow\) tâm I của đường tròn ngoại tiếp luôn nằm trên trung trực BC hay luôn nằm trên Oy
Mà tứ giác ABCO nội tiếp \(\Rightarrow OI=AI\Rightarrow I\) là trung điểm OA (do I, O, A thẳng hàng, cùng nằm trên Oy)
\(\Rightarrow I\left(0;-\dfrac{3m}{4}\right)\)
Mặt khác trung điểm BC cũng thuộc Oy và IB=IC (do I là tâm đường tròn ngoại tiếp)
\(\Rightarrow\) I trùng trung điểm BC
\(\Rightarrow-\dfrac{3m}{4}=-\dfrac{m^2+3m}{2}\) \(\Rightarrow m\)
b.
Từ câu a ta thấy khoảng cách giữa 2 cực đại là:
\(\left|x_B-x_C\right|=2\sqrt{-\dfrac{m}{2}}=5\Rightarrow m=-\dfrac{25}{2}\)
Opps, phần a lý luận bị nhầm lẫn.
Từ việc IB=IC, và trung điểm BC thuộc Oy ko thể dẫn tới kết luận I là trung điểm BC (vì I, B, C ko thẳng hàng)
Do đó phải sửa lại:
\(\left\{{}\begin{matrix}\overrightarrow{IB}=\left(-\sqrt{-\dfrac{m}{2}};\dfrac{-2m^2-3m}{4}\right)\\\overrightarrow{IO}=\left(0;\dfrac{3m}{4}\right)\end{matrix}\right.\)
\(IB=IO\Rightarrow-\dfrac{m}{2}+\left(\dfrac{-2m^2-3m}{4}\right)^2=\left(\dfrac{3m}{4}\right)^2\)
\(\Leftrightarrow m^4+3m^3-2m=0\)
\(\Leftrightarrow m\left(m+1\right)\left(m^2+2m-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}m=0\left(loại\right)\\m=-1\\m=-1+\sqrt{3}\left(loại\right)\\m=-1-\sqrt{3}\end{matrix}\right.\)
Cho hàm số y=f(x) có đồ thị đạo hàm y=f’(x) được cho như hình vẽ bên và các mệnh đề sau:
(1). Hàm số y=f(x) có duy nhất 1 điểm cực trị
(2). Hàm số y=f(x) nghịch biến trên khoảng (-2;1)
(3). Hàm số y=f(x) đồng biến trên khoảng 0 ; + ∞
(4). Hàm số g x = f x + x 2 có 2 điểm cực trị.
Số mệnh đề đúng là
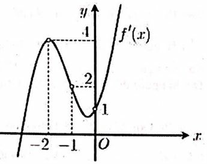
A. 1
B. 3
C. 4
D. 2