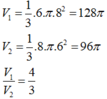Cho ΔABC vuông tại A có AB = 6cm ; AC = 8cm. Vẽ trung tuyến AM.
a, Tính độ dài AM.
b,Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Chứng minh: ΔAMB = ΔDMC
c,Chứng minh: AC vuông góc với DC
d,Chứng minh: AM < \(\frac{AB+CD}{2}\)

Những câu hỏi liên quan
Cho ΔABC vuông tại A, có AH vuông góc BC. Tính AB biết HB = 2cm; HC=8cm, AC=6cm
\(BC=BH+HC=2+8=10\left(cm\right)\)
△ABC vuông tại A có \(BC^2=AB^2+AC^2\\ \Rightarrow AB^2=BC^2-AC^2=10^2-6^2=64\\ \Rightarrow AB=8\left(cm\right)\)
Đúng 2
Bình luận (0)
Cho tam giác ΔABC vuông tại A có AB=6cm,AC=10cm . Đường cao AH a)Chứng minh ΔABC / ΔABH b)Chứng minh AB²=BH.BC c)Tính BC,AH,BH
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó: ΔABC\(\sim\)ΔHBA
b: ta có: ΔABC\(\sim\)ΔHBA
nên BA/BH=BC/BA
hay \(BA^2=BH\cdot BC\)
Đúng 1
Bình luận (0)
a.Xét tam giác ABC và tam giác HBA, có:
^B: chung
^BAC = ^BHA = 90 độ
Vậy tam giác ABC đồng dạng tam giác HBA (g.g)
b.\(\rightarrow\dfrac{AB}{HB}=\dfrac{BC}{AB}\)
\(\Leftrightarrow AB^2=BH.BC\left(đfcm\right)\) (1)
c.Áp dụng định lý pitago \(\Rightarrow BC=\sqrt{6^2+10^2}=2\sqrt{34}\left(cm\right)\)
(1) \(\Leftrightarrow6^2=2\sqrt{34}BH\)
\(\Leftrightarrow BH=\dfrac{9\sqrt{34}}{17}\left(cm\right)\)
Áp dụng định lý pitago trong tam giác ABH \(\Rightarrow AH=\sqrt{6^2-\left(\dfrac{9\sqrt{34}}{17}\right)^2}=\dfrac{15\sqrt{34}}{17}\left(cm\right)\)
Đúng 0
Bình luận (0)
Bài1:Cho ΔMNP vuông tại N. Tính độ dài MN biết MP√30cm,NP√14 cmBài2:Cho ΔABC cân tại A. Biết AB2cm. Tính BCBài3:Cho ΔABC vuông tại A,AH⊥BC tại H. Tính độ dài các cạnh của ΔABC biết AH6cm,HB4cm,HC9cmBài4:Cho ΔABC vuông tại A,AH⊥BC tại H. Tính độ dài các cạnh của ΔABC biết AH4cm,HB2cm,HC8cmBài5:Cho ΔABC vuông tại A,AH⊥BC tại H.Biết AB4cm,HB2cm,HC8cm.Tính BC,AH,ACBài6:Cho ΔABC vuông tại A,AH⊥BC tại H.Biết AB6cm,AC8cm và dfrac{HB}{HC}dfrac{9}{16}Tính HB,HC
Đọc tiếp
Bài1:Cho ΔMNP vuông tại N. Tính độ dài MN biết MP=√30cm,NP=√14 cm
Bài2:Cho ΔABC cân tại A. Biết AB=2cm. Tính BC
Bài3:Cho ΔABC vuông tại A,AH⊥BC tại H. Tính độ dài các cạnh của ΔABC biết AH=6cm,HB=4cm,HC=9cm
Bài4:Cho ΔABC vuông tại A,AH⊥BC tại H. Tính độ dài các cạnh của ΔABC biết AH=4cm,HB=2cm,HC=8cm
Bài5:Cho ΔABC vuông tại A,AH⊥BC tại H.Biết AB=4cm,HB=2cm,HC=8cm.Tính BC,AH,AC
Bài6:Cho ΔABC vuông tại A,AH⊥BC tại H.Biết AB=6cm,AC=8cm và \(\dfrac{HB}{HC}\)=\(\dfrac{9}{16}\)Tính HB,HC
Bài 3:
\(AB=\sqrt{AH^2+BH^2}=\sqrt{6^2+4^2}=2\sqrt{13}\left(cm\right)\)
BC=13cm
=>\(AC=3\sqrt{13}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho ΔABC vuông tại A đường cao AH, có AB=6cm, AC=8cm. Kẻ HM vuông góc với AB (MϵAB), HN (NϵAC).
a) Cm: ΔABC đồng dạng ΔHAC
b) Tính: BC, AH, MN
c) Cm: AB.AM= AC.AN
d) Tính tỉ số dt ANM/ ABC = ? ; Diện tích ANM= ?
giúp mình câu d thui mn ơi :333, mình cám ơn mn ạ
Đúng 0
Bình luận (0)
a) Xét ΔABC vuông tại A và ΔHAC vuông tại H có
\(\widehat{C}\) chung
Do đó: ΔABC\(\sim\)ΔHAC(g-g)
Đúng 1
Bình luận (0)
b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Vậy: BC=10cm
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho ΔABC vuông tại A. Tính AB biết HB = 2cm; HC=8cm, AC=6cm
Anh bổ sung là : AH vuông góc với BC nhé
\(BC=HB+HC=2+8=10\left(cm\right)\)
\(\text{Áp dụng định lý Pytago trong tam giác ABC vuông tại A:}\)
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AB=\sqrt{BC^2-AC^2}=\sqrt{10^2-6^2}=8\left(cm\right)\)
Đúng 1
Bình luận (0)
Bổ sung đề \(AH\) là đường cao.
Áp dụng hệ thức lượng vào tam giác vuông \(ABC\) và đường cao \(AH\) ta có :
\(AB^2=BC.BH\)
\(\Rightarrow AB=\sqrt{BC.BH}=\sqrt{\left(8+2\right).2}=\sqrt{20}=2\sqrt{5}\)\((cm)\)
Đúng 1
Bình luận (0)
Đề bài sai rồi em
Nếu H là chân đường cao trên BC thì tam giác HAC vuông tại H
Khi đó trong tam giác vuông HAC có AC là cạnh huyền và CH là cạnh góc vuông
Nhưng CH=8>AC=6 là hoàn toàn vô lý
Đúng 1
Bình luận (0)
Cho ΔABC vuông tại A có AB = 8cm, AC = 6cm. Vẽ phân giác trong BD và CE. Tính các đoạn thẳng AE,AD,EF,DC.
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=8^2+6^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Xét ΔBAC có BD là phân giác
nên \(\dfrac{AD}{AB}=\dfrac{CD}{CB}\)
=>\(\dfrac{AD}{8}=\dfrac{CD}{10}\)
=>\(\dfrac{AD}{4}=\dfrac{CD}{5}\)
mà AD+CD=AC=6cm(Do D nằm giữa A và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{4}=\dfrac{CD}{5}=\dfrac{AD+CD}{4+5}=\dfrac{6}{9}=\dfrac{2}{3}\)
=>\(AD=4\cdot\dfrac{2}{3}=\dfrac{8}{3}\left(cm\right);CD=5\cdot\dfrac{2}{3}=\dfrac{10}{3}\left(cm\right)\)
Xét ΔCAB có CE là phân giác
nên \(\dfrac{AE}{AC}=\dfrac{BE}{BC}\)
=>\(\dfrac{AE}{6}=\dfrac{BE}{10}\)
=>\(\dfrac{AE}{3}=\dfrac{BE}{5}\)
mà AE+BE=AB=8cm(E nằm giữa A và B)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AE}{3}=\dfrac{BE}{5}=\dfrac{AE+BE}{3+5}=\dfrac{8}{8}=1\)
=>\(AE=3\cdot1=3cm;BE=5\cdot1=5cm\)
Đúng 0
Bình luận (0)
cho ΔABc vuông tại A có đường cao AH. Hãy tính độ đài các đoạn thẳng BH,CH,AH,AC nếu biết AB=6cm,BC=10
Xét ΔABC vuông tại A có
\(AB^2+AC^2=BC^2\)
hay AC=8(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=4,8\left(cm\right)\\BH=3,6\left(cm\right)\\CH=6,4\left(cm\right)\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Cho ΔABC có BC = AC = 5cm, AB = 6cm. Kẻ CH vuông góc AB tại H.
a) Tính độ dài CH.
b) Kẻ HD vuông góc AC tại D, kẻ HE vuông góc CB tại E. Tính độ dài HD và HE.
Cho ΔABC vuông tại A, AB 6cm, AC 8cm. Gọi V1 là thể tích khối nón tạo thành khi quay ΔABC quanh cạnh AB và V2 là thể tích khối nón tạo thành khi quay ΔABC quanh cạnh AC. Tỉ số V1/ V2 bằng A. 4/3 B. 3/4 C. 16/9 D. 64/27
Đọc tiếp
Cho ΔABC vuông tại A, AB = 6cm, AC = 8cm. Gọi V1 là thể tích khối nón tạo thành khi quay ΔABC quanh cạnh AB và V2 là thể tích khối nón tạo thành khi quay ΔABC quanh cạnh AC. Tỉ số V1/ V2 bằng
A. 4/3
B. 3/4
C. 16/9
D. 64/27
cho ΔABC vuông tại A ,vẽ trung tuyến AM,trên tia đối của tia MA lấy điểm E sao cho ME=MA .chứng minh
a/ ΔMBA=ΔMCE
b/AB//CE
c/giả sử AB=6cm,AC=8cm,BC=10cm.So sánh các góc của ΔABC
a: Xét ΔMBA và ΔMCE có
MB=MC
góc BMA=góc CME
MA=ME
=>ΔMBA=ΔMCE
b: ΔMBA=ΔMCE
=>góc MBA=góc MCE
=>AB//CE
c: AB<AC<CB
=>góc C<góc B<góc A
Đúng 0
Bình luận (0)