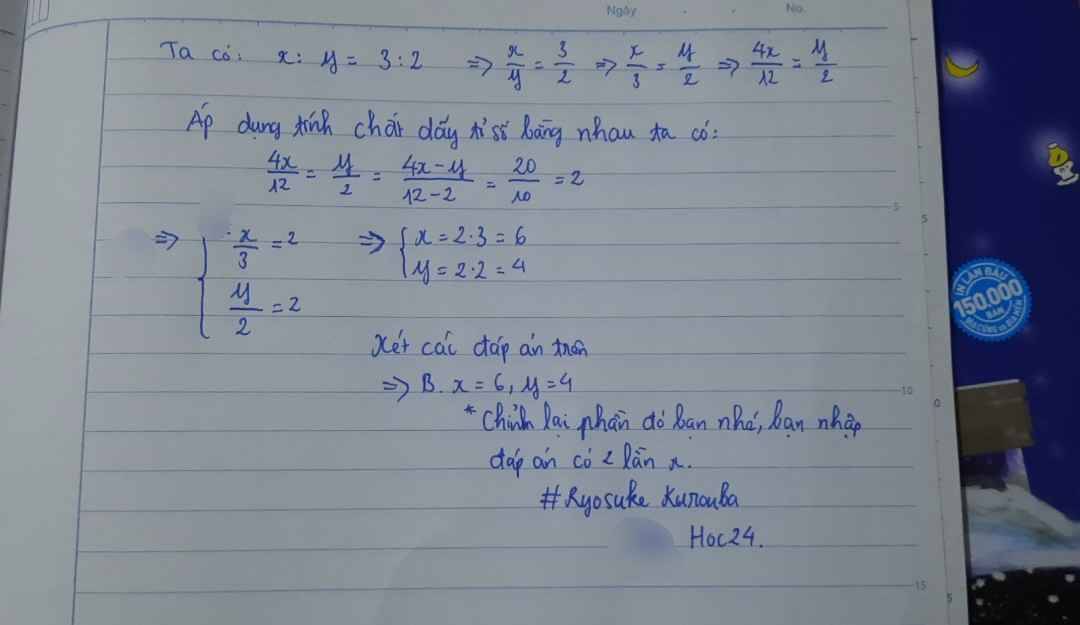x- 6 = y (x+12)

Những câu hỏi liên quan
Câu 32: Cho biết 6𝑥=4𝑦=3𝑧 𝑣à 𝑥+𝑦+𝑧=27 thì giá trị của x ,y, z tìm được là
A. x = 6, y = 9, z = 12 B. x = 6, y = 12, z = 9
C. x = 12, y = 9, z = 6 D. x = 9, y = 12, z = 6
thôi thôi thôi
chị lập tỉ lệ thức đi chị ơi
cũng đến Ạ với chị ý
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Câu 31: Cho dãy tỉ số bằng nhau 𝑥2=𝑦3=𝑧4 và 2𝑥+3𝑦+5𝑧=99 thì giá trị của x ,y, z tìm được là
A. x = 6, y = 9, z = 12 B. x = 6, y = 12, z = 9
C. x = 9, y = 6, z = 12 D. x = 12, y = 6, z = 9
Cho 6 x - 12 y chia 9 = 8 z - 6 x 4 = 12 x - 8 chia 6 Tìm x y z biết 2x + z - y = 36
Xem chi tiết
cekkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkk
Đúng 0
Bình luận (0)
12 x [ y - 6 ] = 4 x y +12
12 . ( y - 6 ) = 4 . y + 12
12y - 72 = 4y + 12
12y - 4y = 12 + 72
8y = 84
y = 12
Vậy y = 12
Đúng 0
Bình luận (0)
12(y-6)=4y+12
<=> 12y-72=4y+12
<=>12y-4y=12+72
<=>8y=84
<=>y=10.5
Đúng 0
Bình luận (0)
\(12\times\left(y-6\right)=4\times y+12\)
\(\Leftrightarrow\)\(12y-72=4y+12\)
\(\Leftrightarrow\)\(12y-4y=12+72\)
\(\Leftrightarrow\)\(8y=84\)
\(\Leftrightarrow\)\(y=10,5\)
Vậy:...........................................................
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm x, y sao cho: a) ( x + 1 ).(2y - 1 )= 12 b) x - 6 = y.(x+12)
12/X=Y/12=135/375
X/9=16/Y=50/75
X/15=Y/12=6/18
X/18=35/45=42/7
tick mk đi xong mk giải cho. mk pít cack làm rùi
Đúng 0
Bình luận (0)
TRẢ LỜI GIÙM MÌNH ĐI , THANKS BẠN RẤT NHIỀU
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
tìm x và y
x+y+12=4√x + 6√(y-1)
ĐK:\(x\ge0;y\ge1\)
\(\Leftrightarrow\left(x-4\sqrt{x}+4\right)+\left(y-1-6\sqrt{y-1}+9\right)=0\)
\(\Leftrightarrow\left(\sqrt{x}-2\right)^2+\left(\sqrt{y-1}-3\right)^2=0\)
Nhận thấy VT\(\ge0\)\(\forall x,y\) thỏa mãn đk
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}\sqrt{x}-2=0\\\sqrt{y-1}=3\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=10\end{matrix}\right.\)(tm)
Vậy...
Đúng 2
Bình luận (0)
Rút gọn biểu thức sau :
12 + 3.y + 4.x + x.y - 12 + 2.y + 6.x - x - 5.y
\(12+3y+4x+xy-12+2y+6x-x-5y\)
\(=9x+xy\)
\(=x\left(y+9\right)\)
Đúng 0
Bình luận (0)
12+3y+4x+xy-12+2y+6x-x-5y=
=9x+xy
=x(9+y)
Đúng 0
Bình luận (0)
12 + 3y + 4x + xy -12 + 2y + 6x- x - 5y
=9x +xy
=x(y+9)
Đúng 0
Bình luận (0)
cho rằng x:y=3:2 và4x-y=20.Giá trị của x và y bằng A.x=12;y=8 B.x=6;x=4 C.x=8;y=12 D.x=4;y=6
Lời giải:
Đặt $\frac{x}{3}=\frac{y}{2}=t$
$\Rightarrow x=3t; y=2t$. Thay vô điều kiện $4x-y=20$ ta có:
$4.3t-2t=20$
$\Leftrightarrow 10t=20\Leftrightarrow t=2$
$\Rightarrow x=3t=6; y=2t=4$
Đúng 2
Bình luận (0)
Giả sử x và y là hai đại lượng tỉ lệ thuận x1, x2; là hai giá trị khác nhau của x và y1, y2 là hai giá trị tương ứng của y. Tính x1, y1 biết 2y1 + 3x1 24, x2 -6, y2 -3A. x1 12; y1 6B. x1 -12; y1 -6C. x1 12; y1 -6D. x1 -12; y1 6
Đọc tiếp
Giả sử x và y là hai đại lượng tỉ lệ thuận x1, x2; là hai giá trị khác nhau của x và y1, y2 là hai giá trị tương ứng của y. Tính x1, y1 biết 2y1 + 3x1 = 24, x2 = -6, y2 = -3
A. x1 = 12; y1 = 6
B. x1 = -12; y1 = -6
C. x1 = 12; y1 = -6
D. x1 = -12; y1 = 6
Do x và y là hai đại lượng tỉ lệ thuận và \(x_1,x_2\)là hai giá trị khác nhau của x;\(y_1,y_2\)là hai giá trị tương ứng của y nên
\(\frac{y_1}{y_2}=\frac{x_1}{x_2}=\frac{2y_1}{2y_2}=\frac{3x_1}{3x_2}=\frac{2y_1+3x_1}{2y_2+3x_2}\)
Vì \(x_2=-6,y_2=-3\)và \(2y_1+3x_1=24\)nên ta có :
\(\frac{y_1}{-3}=\frac{x_1}{-6}=\frac{2y_1+3x_1}{2\cdot\left(-3\right)+3\cdot\left(-6\right)}=\frac{24}{-24}=-1\)
=> \(y_1=\left(-1\right)\cdot\left(-3\right)=3;x_1=\left(-1\right)\cdot\left(-6\right)=6\)