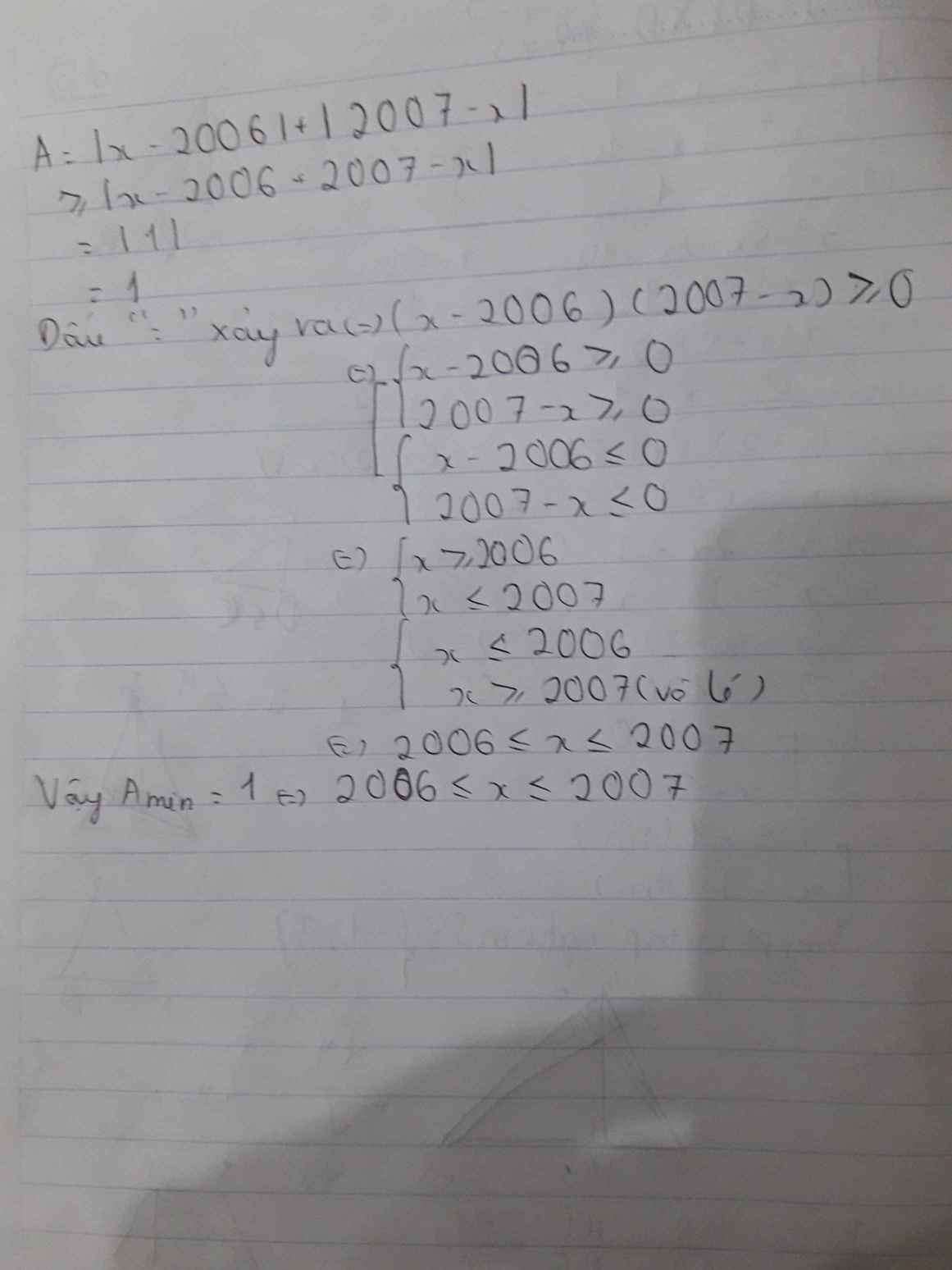\(A=\left|x-2006\right|+\left|2007-x\right|\ge\left|x-2006+2007-x\right|=\left|1\right|=1\)

\(minA=1\Leftrightarrow\left(x-2006\right)\left(2007-x\right)\ge0\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-2006\ge0\\2007-x\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x-2006\le0\\2007-x\le0\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow2006\le x\le2007\)

\(A=\left|x-2006\right|+\left|2007-x\right|\)

Vì \(x>2007\) nên \(2x-4013>4014-4013=1\)

\(\Rightarrow A>1\)

Vậy \(A_{min}=1\Leftrightarrow2006\le x\le2007\)

Áp dụng bđt \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\)
\(A\ge\left|x-2016+2017-x\right|=1\)
Vậy minA=1

Ta có \(A=\left|x-2006\right|+\left|2007-x\right|\)

\(=\left|2006-x\right|+\left|x-2007\right|\)

Ta có \(A=\left|2006-x\right|+\left|x-2007\right|\ge\left|2006-x+x-2007\right|=1\)

Dấu "=" xảy ra khi và chỉ \(2006\le x\le2007\)

Vậy GTNN A=1 khi \(2006\le x\le2007\)

Ta có : \(A=\left|x-2006\right|+\left|2007-x\right|\)

\(=\left|2006-x\right|+\left|x-2007\right|\)

Ta có : \(A=\left|x-2006\right|+\left|2007-x\right|\ge\left|2006-x+x-2007\right|=1\)

Dấu " = " xảy ra khi và chỉ \(2006\le x\le2007\)

Vậy GTNN \(A=1\)khi \(2006\le x\le2007\)