Cho tam giác ABC nhọn.Vẽ về phía ngoài của tam giác ABC các tam giác vuông cân ABD và ACE, tại A kẻ đường cao AH( H € BC).Chứng minh AH đi qua trung điểm của DE
Cho tam giác ABC. Vẽ về phía ngoài của tam giác ABC các tam giác vuông cân tại A là tam giác ABD và tam giác ACE. Kẻ AH vuông góc với BC, Kẻ DM vuông góc với AH, EN vuông góc với AH. Chứng minh
a) DM=AH
b) MN đi qua trung điểm của DE
c) Tam giác DAC= tam giác BAE
a, có góc ADM+DAM=90độ
có góc DAM+DAB+BAH=90độ
=>DAM+BAH=90 độ=>BAH=ADM
có DAM+ADM=90 độ
có BAH+ABH=90 độ
mà ADM=BAH=>ABH=DAM
xét tg DAM và tg BAH
AB=AD
góc ADM=BAH => tg DAM=tg ABH(g.c.g)
góc DAM=ABH
=> DM=AH(2 cạnh t/ứ)
b, nối D,E
xét tg NEA và tg AHC giống ý a, rùi có NE=AH mà DM=AH => DM=NE
gọi giao điểm của DE và NA là T => NTE=DTM(đối đỉnh)
Xét tg MDT và tg NET
NE=DM
NET=TDM(2 góc kia = nhau thì góc này =) => tgMTD=tgNET(g.c.g)
ENT=DMT(=90 độ)
=> DT=ET(2 cạnh t.ứ)=> MN đi qua trung điểm của DE
c, có EAC=DAB(=90độ)=> EAC+BAC=DAB+BAC(1)
DA=BA(2), CA=EA(3)
từ 1,2 3 => 2 tg đó = nhau
Cho tam giác nhọn ABC. Vẽ về phía ngoài tam giác các tam giác ABD; ACE vuông cân tại A. Vẽ đường cao AH của tam giác ABC. C/m AH đi qua trung điểm O của DE
Cho tam giác ABC nhọn.Vẽ về phía ngoài ΔABC các tam giác ABD và ACE đều vuông cân tại A .AH vuông góc BC.DI và EK vuông góc với đường thẳng AH(I,K thuộc đường thẳng AH).CMR
a,tam giác ABH=tam giác DAI
b,DI=EK
c,Cm AH cắt DE tại trung điểm DE
Dễ nhưng dài nên lười đánh máy quá:")
a) Ta có: \(\widehat{BAH}+\widehat{ABH}=90^o\)
Mà \(\widehat{DAI}+\widehat{DAB}+\widehat{BAH}=180^O\)
\(\Leftrightarrow\widehat{DAI}+90^o+\widehat{BAH}=180^O\)
\(\Leftrightarrow\widehat{DAI}+\widehat{BAH}=90^o\)
=> \(\widehat{DAI}=\widehat{ABH}\)( cùng phụ BAH)
Xét ∆ABH và ∆DAI:
AB=AD(∆ABD vuông cân tại A)
\(\widehat{AHB}=\widehat{DIA}=90^o\)
\(\widehat{ABH}=\widehat{DAI}\left(cmt\right)\)
=>∆ABH=∆DAI (ch.gn)
b) Theo câu a: ∆ABH=∆DAI
=> AH=DI (2 cạnh t/ứ)(1)
Cmtt câu a ta được ∆AKE=∆CHA
=> EK=AH (2 canh t/ứ) (2)
Từ (1) và (2) suy ra DI=EK
c) Gọi giao điểm của DE và HA là F
Xét ∆FID và ∆FKE:DI=K (cm ở câu b)
\(\widehat{FID}=\widehat{FKE}=90^o\)
\(\widehat{IFD}=\widehat{KFE}\) (2 góc đối đỉnh)
=> ∆FID=∆FKE (cgv.gn)
=> DF=EF (2 canh t/ứ)
=> F là trung điểm của DE
=> AH cắt DE tại trung điểm của DE
Cho tam giác ABC nhọn.Vẽ về phía ngoài ΔABC các tam giác ABD và ACE đều vuông cân tại A .AH vuông góc BC.DI và EK vuông góc với đường thẳng AH(I,K thuộc đường thẳng AH).CMR
a,tam giác ABH=tam giác DAI
b,DI=EK
c,Cm AH cắt DE tại trung điểm DE
cho tam giác ABC, vẽ ra phía ngoài tam giác ABC các tam giác vuông cân ABD và ACE( cân tại A). AH vuông với BC, M là trung điểm của BC
a. CM AH đi qua trung điểm của DE
b. CM đường thẳng AM vuông góc với DE
a: Vẽ DI,EK vuông góc AH
Xét ΔIDA và ΔHAB có
góc DIA=góc AHB
AD=AB
góc A1=góc ABH(=90 độ-góc A2)
=>ΔIDA=ΔHAB
=>ID=AH(1)
Xét ΔKAE và ΔHCA có
góc EKA=góc AHC
AE=AC
góc EAK=góc HCA
=>ΔKAE=ΔHCA
=>AH=EK=DI
Gọi giao của AH và DE là N
Xét ΔDIN và ΔKEN co
góc DIN=góc EKN
DI=EK
góc ENK=góc DNK
=>ΔDIN=ΔKEN
=>EN=DN
=>N là trung điểm của DE
b: Lấy F đối xứng A qua M
Xet ΔAMB và ΔFMC có
MA=MF
góc AMB=góc FMC
MB=MC
=>ΔAMB=ΔFMC
=>AB=CF và góc B=góc FCM
=>góc ACF=góc ACB+góc B=180 độ-góc BAC
Gọi giao của AM và DE là I
Xet ΔACF và ΔEAD có
AC=ED
CF=AD
góc EAD=góc ACF
=>ΔACF=ΔEAD
=>AF=DE
=>AM=1/2DE
ΔAMB=ΔFMC
=>góc BAM=góc MFC
ΔACF=ΔEAD
=>góc MFC=góc EDA
=>góc BAM=góc EDA
=>góc EDA+góc DAI=90 độ
=>AM vuông góc DE
Cho tam giác ABC,ở phía ngoài tam giác đó ta vẽ các tam giác vuông cân là tam giác ABD và tam giác ACE
a, Chứng minh CD=DE và CD vuông góc với BE
b, Kẻ đường thẳng đi qua A và vuông góc với BC tại H
Chứng minh đường thẳng AH đi qua trung điểm của DE
a) Ta có: gócDAB+gócBAC=gócDAC
gócEAC+gócBAC=gócBAE
MÀ gócDAB=gócEAC(=90độ)
=> gócDAC=gócBAE
xét tam giác DAC và tam giác BAE có:
AD=AB(GT)
AE=AC(GT)
gócDAC=gócBAE(cmt)
=>tam giác DAC =tam giác BAE(c.g.c)
gọi giao điểm của AB và CD là F
giao điểm của BE VÀ CD là I
Xét tam giác afd vuông tại A
=>gócADF+gócDFA=90độ
mà gócADF= gócABI ( tam giác DAC =tam giác BAE )
gócDFA=gócBFI
=> gócABI+gócBFI=90độ
=>gócFIB=90độ
=>CD vuông góc BE
b)từ a
có KH,BE,CD là 3 đường cao của tam giácKBC nên chúng đồng quy tại I
a) Kẻ DM, EN vuông góc BC.
Xét :
_ AC = CE
_
_ (góc có cạnh tương ứng vuông góc)
Nên chúng bằng nhau, suy ra:
Tương tự:
Do (P là giao của CK và BE, quên vẽ) nên CNEP là tứ giác ntiếp
Do đó 2 tam giác vuông
Từ đó:
2 tg này có 2 cặp cạnh tg ứng vuông góc là MD, BH và MC, KH nên cặp còn lại
b) Từ a ta có KH, BE, CD là 3 đường cao , nên chúng đòng quy tại I.

a) Kẻ DM, EN vuông góc BC.
Xét :
AC = CE
(góc có cạnh tương ứng vuông góc)
Nên chúng bằng nhau, suy ra:
Tương tự:
Do (P là giao của CK và BE, quên vẽ) nên CNEP là tứ giác ntiếp
Do đó 2 tam giác vuông
Từ đó:
2 tg này có 2 cặp cạnh tg ứng vuông góc là MD, BH và MC, KH nên cặp còn lại
b) Từ a ta có KH, BE, CD là 3 đường cao , nên chúng đòng quy tại I.
Cho tam giác ABC. Vẽ ở phía ngoài tam giác ABC các tam giác vuông tại A và ABD, ACE có AB = AD, AC = AE. Kẻ AH vuông góc với BC, DM vuông góc với AH, EN vuông góc với AH. Chứng minh rằng: MN đi qua trung điểm của DE
Ta có: ∠(HAC) +∠(CAE) +∠(EAN) =180o(kề bù)
Mà ∠(CAE) =90o⇒∠(HAC) +∠(EAN) =90o (4)
Trong tam giác vuông AHC, ta có:
∠(AHC) =90o⇒∠(HAC) +∠(HCA) =90o (5)
Từ (4) và (5) suy ra: ∠(HCA) =∠(EAN) ̂
Xét hai tam giác vuông AHC và ENA, ta có:
∠(AHC) =∠(ENA) =90o
AC = AE (gt)
∠(HCA) =∠(EAN) ( chứng minh trên)
Suy ra : ΔAHC= ΔENA(cạnh huyền, góc nhọn)
Vậy AH = EN (hai cạnh tương ứng)
Từ (3) và (6) suy ra: DM = EN
Vì DM ⊥ AH và EN ⊥ AH (giả thiết) nên DM // EN (hai đường thẳng cùng vuông góc với đường thẳng thứ ba)
Gọi O là giao điểm của MN và DE
Xét hai tam giác vuông DMO và ENO, ta có:
∠(DMO) =∠(ENO) =90o
DM= EN (chứng minh trên)
∠(MDO) =∠(NEO)(so le trong)
Suy ra : ΔDMO= ΔENO(g.c.g)
Do đó: DO = OE ( hai cạnh tương ứng).
Vậy MN đi qua trung điểm của DE
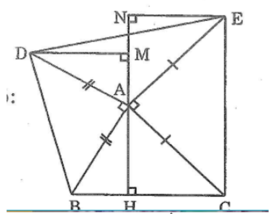
Cho tam giác ABC nhọn. Ở phía ngoài tam giác, vẽ tam giác vuông cân: Tam giác ABD và tam giác ACE. Kẻ AH vuông góc BC tại H. Từ D và E kẻ DI, EK lần lượt vuông góc với AH
A,Chứng minh DI=AH
B,Chứng minh A,H, trung điểm của DE thẳng hàng
C, Gọi M là trung điểm của BC. Chứng minh: AM vuông góc DE
Cho tam giác ABC,ở phía ngoài tam giác đó ta vẽ các tam giác vuông cân là tam giác ABD và tam giác ACE
a, Chứng minh CD=DE và CD vuông góc với BE
b, Kẻ đường thẳng đi qua A và vuông góc với BC tại H
Chứng minh đường thẳng AH đi qua trung điểm của DE
(Vẽ hình hộ mik nha)
a)kẻ DM,EN vuông góc BC
Xét tam giác AHC và tam giác CNE có:
AC=CE
góc AHC= góc CNE=90
góc ACH=góc CEN
suy ra AH=CN
HC=NE
tương tự:AH=BM
HB=MB
do góc CNE=góc CPE( p là giao của CK và BE)
suy ra góc NEB=HCK
Tam giác BNE=KHC
suy ra BN=Kn suy ra BC=KA
suy ra CM=KN
suy ra tam giác CMD=KHB
có 2 cặp góc vuông tương ứng
MD,BH và MC,KN
suy ra CD vuông BK
b)từ a
có KH,BE,CD là 3 đường cao của tam giácKBC nên chúng đồng quy tại I
a) Ta có: gócDAB+gócBAC=gócDAC
gócEAC+gócBAC=gócBAE
MÀ gócDAB=gócEAC(=90độ)
=> gócDAC=gócBAE
xét tam giác DAC và tam giác BAE có:
AD=AB(GT)
AE=AC(GT)
gócDAC=gócBAE(cmt)
=>tam giác DAC =tam giác BAE(c.g.c)
gọi giao điểm của AB và CD là F
giao điểm của BE VÀ CD là I
Xét tam giác afd vuông tại A
=>gócADF+gócDFA=90độ
mà gócADF= gócABI ( tam giác DAC =tam giác BAE )
gócDFA=gócBFI
=> gócABI+gócBFI=90độ
=>gócFIB=90độ
=>CD vuông góc BE