3 – 4x(25 – 2x) = 8x2 + x – 300

⇔ 3 – 4x.25 + 4x.2x = 8x2 + x – 300

⇔ 3 – 100x + 8x2 = 8x2 + x – 300

⇔ -100x – x = -300 – 3

⇔ -101x = -303

⇔ x = 3.

Vậy phương trình có tập nghiệm S = {3}.

`b,2(x+1)=5x-7`

`=>2x+2=5x-7`

`=>3x=9`

`=>x=3`

`c,3-4x(25-2x)=8x^2+x-300`

`<=>3-100x+8x^2=8x^2+x-300`

`<=>101x=303`

`<=>x=3`

`d,(10x+3)/12=1+(6+8x)/9`

`<=>(10x+3)/12=(8x+15)/9`

`<=>30x+9=32x+60`

`<=>2x=-51`

`<=>x=-51/2`

a) \(PT\Leftrightarrow3x-2x=2-3\Leftrightarrow x=-1\)

Vậy: \(S=\left\{-1\right\}\)

b) \(PT\Leftrightarrow-2x+3x=-7+22\Leftrightarrow x=15\)

Vậy: \(S=\left\{15\right\}\)

c) \(PT\Leftrightarrow8x-5x=3+12\Leftrightarrow3x=15\Leftrightarrow x=5\)

Vậy: \(S=\left\{5\right\}\)

d) \(PT\Leftrightarrow x+4x-2x=12+25-1\Leftrightarrow3x=36\Leftrightarrow x=12\)

Vậy: \(S=\left\{12\right\}\)

e) \(PT\Leftrightarrow x+2x+3x-3x=19+5\Leftrightarrow3x=24\Leftrightarrow x=8\)

Vậy: \(S=\left\{8\right\}\)

a)3x-2=2x-3

=>x=-1

b)7-2x=22-3x

=>x=15

c)8x-3=5x+12

=>3x=15

=>x=5

d)x-12+4x=25+2x-1

=>3x=12

=>x=4

e)x+2x+3x-19=3x+5

=>3x=24

=>x=8

a)3x-2=2x-3

=>x=-1

b)7-2x=22-3x

=>x=15

c)8x-3=5x+12

=>3x=15

=>x=5

d)x-12+4x=25+2x-1

=>3x=36

=>x=12

e)x+2x+3x-19=3x+5

=>3x=24

=>x=8

a) Xét tam thức \(f\left( x \right) = 7{x^2} - 19x - 6\) có \(\Delta  = 529 > 0\), có hai nghiệm phân biệt \({x_1} =  - \frac{2}{7},{x_2} = 3\) và có \(a = 7 > 0\)

Ta có bảng xét dấu như sau

Vậy nghiệm của bất phương trình là đoạn \(\left[ { - \frac{2}{7};3} \right]\)

b) \( - 6{x^2} + 11x > 10 \Leftrightarrow  - 6{x^2} + 11x - 10 > 0\)

Xét tam thức \(f\left( x \right) =  - 6{x^2} + 11x - 10\) có \(\Delta  =  - 119 < 0\)và có \(a =  - 6 < 0\)

Ta có bảng xét dấu như sau

Vậy bất phương trình vô nghiệm

c) \(3{x^2} - 4x + 7 > {x^2} + 2x + 1 \Leftrightarrow 2{x^2} - 6x + 6 > 0\)

Xét tam thức \(f\left( x \right) = 2{x^2} - 6x + 6\) có \(\Delta  =  - 12 < 0\)và có \(a = 2 > 0\)

Ta có bảng xét dấu như sau

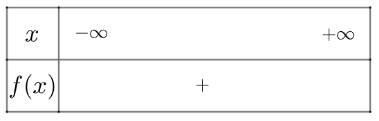
Vậy bất phương trình có vô số nghiệm

d) Xét tam thức \(f\left( x \right) = {x^2} - 10x + 25\) có \(\Delta  = 0\), có nghiệm kép \({x_1} = {x_2} = 5\) và có \(a = 1 > 0\)

Ta có bảng xét dấu như sau

Vậy nghiệm của bất phương trình là \(x = 5\)

\(a,5^{2x-1}=25\\ \Leftrightarrow5^{2x-1}=5^2\\ \Leftrightarrow2x-1=2\\ \Leftrightarrow2x=3\\ \Leftrightarrow x=\dfrac{3}{2}\)

\(b,3^{x+1}=9^{2x+1}\\ \Leftrightarrow3^{x+1}=3^{4x+2}\\ \Leftrightarrow x+1=4x+2\\ \Leftrightarrow3x=-1\\ \Leftrightarrow x=-\dfrac{1}{3}\)

\(c,10^{1-2x}=100000\\ \Leftrightarrow10^{1-2x}=10^5\\ \Leftrightarrow1-2x=5\\ \Leftrightarrow2x=-4\\ \Leftrightarrow x=-2\)

Bài 1: Giải các phương trình sau:

a) 3(2,2-0,3x)=2,6 + (0,1x-4)

<=> 6.6 - 0.9x = 2,6 + 0,1x - 4

<=> - 0.9x - 0,1x = -6.6 -1,4

<=> -x = -8

<=> x = 8

Vậy x = 8

b) 3,6 -0,5 (2x+1) = x - 0,25(22-4x)

<=> 3,6 - x - 0,5 = x - 5,5 + x

<=> - x - 3,1 = -5,5

<=> - x = -2.4

<=> x = 2.4

Vậy  x = 2.4

a. (3x - 1)² - (x + 3)² = 0

\(\Leftrightarrow\left(3x-1+x+3\right)\left(3x-1-x-3\right)=0\)

\(\Leftrightarrow\left(4x+2\right)\left(2x-4\right)=0\)

\(\Leftrightarrow4x+2=0\)  hoặc  \(2x-4=0\)

1. \(4x+2=0\Leftrightarrow4x=-2\Leftrightarrow x=-\dfrac{1}{2}\)

2. \(2x-4=0\Leftrightarrow2x=4\Leftrightarrow x=2\)

S=\(\left\{-\dfrac{1}{2};2\right\}\)

b. \(x^3=\dfrac{x}{49}\)

\(\Leftrightarrow49x^3=x\)

\(\Leftrightarrow49x^3-x=0\)

\(\Leftrightarrow x\left(49x^2-1\right)=0\)

\(\Leftrightarrow x\left(7x+1\right)\left(7x-1\right)=0\)

\(\Leftrightarrow x=0\) hoặc  \(7x+1=0\) hoặc \(7x-1=0\)

1. x=0

2. \(7x+1=0\Leftrightarrow7x=-1\Leftrightarrow x=-\dfrac{1}{7}\)

3. \(7x-1=0\Leftrightarrow7x=1\Leftrightarrow x=\dfrac{1}{7}\)

*Cách khác:

a) Ta có: \(\left(3x-1\right)^2-\left(x+3\right)^2=0\)

\(\Leftrightarrow\left(3x-1\right)^2=\left(x+3\right)^2\)

\(\Leftrightarrow\left[{}\begin{matrix}3x-1=-x-3\\3x-1=x+3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}4x=-2\\2x=4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=2\end{matrix}\right.\)

Vậy: \(S=\left\{-\dfrac{1}{2};2\right\}\)

a: =>(x-2)(2x+5)=0

=>x-2=0 hoặc 2x+5=0

=>x=2 hoặc x=-5/2

c: \(\dfrac{2x}{x-1}-\dfrac{x}{x+1}=1\)

=>\(\dfrac{2x^2+2x-x^2+x}{x^2-1}=1\)

=>x^2+3x=x^2-1

=>3x=-1

=>x=-1/3

\(a,\Leftrightarrow\left(x-2\right)\left(2x+5\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}x-2=0\\2x+5=0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=2\\x=\dfrac{5}{2}\end{matrix}\right.\)

Vậy phương trình có tập nghiệm S = \(\left\{2;\dfrac{5}{2}\right\}\)

\(c,\Leftrightarrow2x.\left(x+1\right)-x.\left(x-1\right)=\left(x-1\right)\left(x+1\right)\)              ( ĐKXĐ: \(x\ne-1;x\ne1\) )

\(\Leftrightarrow2x^2+2x-x^2+x=x^2-1\\ \Leftrightarrow x^2-x^2+3x=-1\\ \Leftrightarrow3x=-1\\ \Leftrightarrow x=-\dfrac{1}{3}\)  ( nhận )

Vậy phương trình có tập nghiệm S = \(\left\{-\dfrac{1}{3}\right\}\)