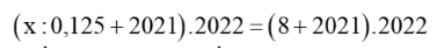
Tìm x ạ
Tìm x: (x-3)(x-1)-x(x-2)=0 (x+2y)²-(2x-y)² [Giúp mình ạ vs ạ]
a: (x-3)(x-1)-x(x-2)=0
=>\(x^2-4x+3-x^2+2x=0\)
=>\(-2x+3=0\)
=>-2x=-3
=>\(x=\dfrac{3}{2}\)
b: \(\left(x+2y\right)^2-\left(2x-y\right)^2\)
\(=\left(x+2y+2x-y\right)\left(x+2y-2x+y\right)\)
\(=\left(3x+y\right)\left(-x+3y\right)\)
tìm x(x:32+15):4=24 cíu tui ạ cảm ơn ạ
\(\left(x:32+15\right):4=24\)
\(x:32+15=24.4\)
\(x:32+15=96\)
\(x:32=96-15\)
\(x:32=81\)
\(x=81.32\)
\(x=2592\)
Sửa bài
\(\left(x:32+15\right):4=24\)
\(x:32+15=24.4\)
\(x:32+15=6\)
\(x:32=6-15\)
\(x:32=-9\)
\(x=\left(-9\right).32\)
\(x=-288\)
Bạn bỏ bài viết trên đi nhé. Dưới mới đúng á
Mn ơiiiiiiii giúp mình với ạ!!
Tìm x:
(-5).(x-2015)<0
Thanks mn ạ!!!!!![]()
\(\Leftrightarrow x-2015>0\left(-5< 0\right)\\ \Leftrightarrow x>2015\)
câu 8 : tìm x :
a) x x 5,8 = 19,72
b) x : 5,6 = 34,5
làm giúp em vói ạ ! em cám ơn ạ !
a, x x 5,8=19,72
x=19,72:5,8
x=3.4
b,x:5,6=34,5
x=34,5 x 5,6
x=193,2
tìm x(2x-6).(5-x)=0 giúp tui vs ạ cảm ơn ạ:33
\(\left(2x-6\right)\times\left(5-x\right)=0\)
\(2x-6=0;5-x=0\)
\(x=3;x=5\)
Vậy: \(x=3;x=5\)
Tìm hai số x,y biết :
b, x : 2 = y : (-5) và x - y = -7
d, 4 : x = 7 : y và y - x = -12
giúp mình vs ạ , mình cần gấp ạ , cảm ơn nhiều ạ !
Áp dụng dãy tỉ số bằng nhau:
b.
\(\dfrac{x}{2}=\dfrac{y}{-5}=\dfrac{x-y}{2-\left(-5\right)}=\dfrac{-7}{7}=-1\)
\(\Rightarrow\left\{{}\begin{matrix}x=2.\left(-1\right)=-2\\y=-5.\left(-1\right)=5\end{matrix}\right.\)
d.
\(\dfrac{4}{x}=\dfrac{7}{y}\Rightarrow\dfrac{y}{7}=\dfrac{x}{4}=\dfrac{y-x}{7-4}=\dfrac{-12}{3}=-4\)
\(\Rightarrow\left\{{}\begin{matrix}x=4.\left(-4\right)=-16\\y=7.\left(-4\right)=-28\end{matrix}\right.\)
tìm x
a)(x-8)(x^3+8)=0
b)(4x-3)-(x+5)=3(10-x)
giúp mình với ạ đang cần gấp ạ
\(a,\Leftrightarrow\left[{}\begin{matrix}x-8=0\\x^3+8=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=8\\x^3=-8\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=8\\x=-2\end{matrix}\right.\\ b,\Leftrightarrow4x-3-x-5=30-3x\\ \Leftrightarrow4x-x+3x=30+5+3\\ \Leftrightarrow6x=38\\ \Leftrightarrow x=\dfrac{19}{3}\)
Tìm x,y thuộc N biết:
2xy+x+2y=13
Giúp mik với ,mik cần gấp ạ!Cảm ơn ạ!
\(2xy+x+2y=13\\ \Rightarrow2xy+x+2y+1-1=13\\ \Rightarrow\left(2xy+2y\right)+\left(x+1\right)=13+1\\ \Rightarrow2y\left(x+1\right)+\left(x+1\right)=14\\ \Rightarrow\left(x+1\right)\left(2y+1\right)=14\\ \Rightarrow\left(x+1\right);\left(2y+1\right)\inƯ\left(14\right)\\ \Rightarrow\left(x+1\right);\left(2y+1\right)\in\left\{-14;-7;-2;-1;1;2;7;14\right\}\)
| \(x+1\) | \(-14\) | \(-7\) | \(-2\) | \(-1\) | \(1\) | \(2\) | \(7\) | \(14\) |
| \(2y+1\) | \(-1\) | \(-2\) | \(-7\) | \(-14\) | \(14\) | \(7\) | \(2\) | \(1\) |
| \(x\) | \(-15\) | \(-8\) | \(-3\) | \(-2\) | \(0\) | \(1\) | \(6\) | \(13\) |
| \(y\) | \(-1\) | \(-\dfrac{3}{2}\) | \(-4\) | \(-\dfrac{15}{2}\) | \(\dfrac{13}{2}\) | \(3\) | \(\dfrac{1}{2}\) | \(0\) |
Vì \(x,y\in N\Rightarrow\left(x;y\right)=\left(0;\dfrac{13}{2}\right),\left(1;3\right),\left(6;\dfrac{1}{2}\right),\left(13;0\right)\)
Vậy \(\left(x;y\right)=\left(0;\dfrac{13}{2}\right),\left(1;3\right),\left(6;\dfrac{1}{2}\right),\left(13;0\right)\)
tìm x, biết :
a, x/6 = 8/3
b, 5/x = 4/9
c, x + 3/ - 4 = 5/20
d, 7/ 3 + 4x = -2/9
f, 3/ x - 1 = x - 1/ 27
giúp e vs ạ , e cần gấp ạ , e cảm ơn nhiều ạ
a: \(\dfrac{x}{6}=\dfrac{8}{3}\)
=>\(x=6\cdot\dfrac{8}{3}=\dfrac{6}{3}\cdot8=8\cdot2=16\)
b: \(\dfrac{5}{x}=\dfrac{4}{9}\)
=>\(x=\dfrac{5\cdot9}{4}=\dfrac{45}{4}\)
c: \(\dfrac{x+3}{-4}=\dfrac{5}{20}\)
=>\(x+3=\dfrac{-4\cdot5}{20}=-1\)
=>x=-1-3=-4
d: \(\dfrac{7}{3+4x}=\dfrac{-2}{9}\)
=>\(4x+3=\dfrac{9\cdot7}{-2}=-\dfrac{63}{2}\)
=>\(4x=-\dfrac{63}{2}-3=-\dfrac{69}{2}\)
=>\(x=-\dfrac{69}{8}\)
f: ĐKXĐ: x<>1
\(\dfrac{3}{x-1}=\dfrac{x-1}{27}\)
=>\(\left(x-1\right)^2=3\cdot27=81\)
=>\(\left[{}\begin{matrix}x-1=9\\x-1=-9\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=10\left(nhận\right)\\x=-8\left(nhận\right)\end{matrix}\right.\)
1.Tìm GTNN của Bthức : B= 4x2- 6x+1 : (x-2)2 với x ≠ 2
2. Tìm GTLN của Bthức: C= x2 + 4x - 14 : x2 -2x +1 với x≠ 1
giúp mình với ạ, mình cảm ơn nhiều ạ
1.
Đặt \(x-2=t\ne0\Rightarrow x=t+2\)
\(B=\dfrac{4\left(t+2\right)^2-6\left(t+2\right)+1}{t^2}=\dfrac{4t^2+10t+5}{t^2}=\dfrac{5}{t^2}+\dfrac{2}{t}+4=5\left(\dfrac{1}{t}+\dfrac{1}{5}\right)^2+\dfrac{19}{5}\ge\dfrac{19}{5}\)
\(B_{min}=\dfrac{19}{5}\) khi \(t=-5\) hay \(x=-3\)
2.
Đặt \(x-1=t\ne0\Rightarrow x=t+1\)
\(C=\dfrac{\left(t+1\right)^2+4\left(t+1\right)-14}{t^2}=\dfrac{t^2+6t-9}{t^2}=-\dfrac{9}{t^2}+\dfrac{6}{t}+1=-\left(\dfrac{3}{t}-1\right)^2+2\le2\)
\(C_{max}=2\) khi \(t=3\) hay \(x=4\)