Cho Hinh Thang ABCD(AB//CD).Biet AB=2,5cm,AD=3,5cm,BD=5cm;va Goc DAB=DAC.
a)Chung Minh Hai Tam Giac ADB va BCD Đồng Dạng.
b)Tính Độ Dài các cạnh BC và CD
c)Tinh Tỉ Số dien tich 2 tam giac ADB và BCD.
cho hinh thang ABCD(AB//CD) . biet AB=2,5cm AD=3,5cm BD=5cm va goc DAB=DBC
cchung minh 2 tam giac ADB va BCD dong dang
tinh BC va CD
TINH TI SO DIEN TICH 2 tam giac ADB va BCD
cho hinh thang ABCD(ab//cd).biet ab=2,5cm , ad=3,5cm, bd=5cm, va goc dab=dbc
ch/m 2tam giac adb va bcd dong dang
tinh do dai cac canh bc va cd
tinh ti so dien tich cua 2 tam giac adb va bcd
Hình thang ABCD (AB // CD) có AB =2,5cm, AD = 3,5cm, BD=5cm và ∠ (DAB) = ∠ (DBC). Tính độ dài BC, CD.
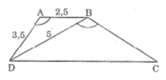
Vì
△
ABD ∼
△
BDC nên: 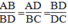
Với AB = 2,5cm; AD = 3,5cm; BD = 5cm, ta có:
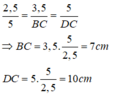
Hình thang ABCD (AB // CD) có AB =2,5cm, AD = 3,5cm, BD=5cm và ∠ (DAB) = ∠ (DBC). Chứng minh tam giác ADB đồng dạng với tam giác BCD.
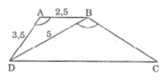
Xét △ ABD và △ BDC, ta có:
∠ (DAB) = ∠ (DBC) (gt)
∠ (ABD) = ∠ (BDC) (so le trong)
Suy ra: △ ABD ∼ △ BDC (g.g)
Cho hình thang ABCD (AB //CD). Biết AB = 2,5cm; AD = 3,5cm; BD = 5cm; và góc DAB = DBC.
a) Chứng minh hai tam giác ADB và BCD đồng dạng.
b) Tính độ dài các cạnh BC và CD
a: Xét ΔADB và ΔBCD có
góc DAB=góc CBD
góc ABD=góc BDC
=>ΔADB đồng dạng với ΔBCD
b: ΔADB đồng dạng với ΔBCD
=>AD/BC=DB/CD=AB/BD
=>3,5/BC=5/CD=2,5/5=1/2
=>BC=7cm; CD=10cm
Hình thang ABCD (AB // CD) có AB =2,5cm, AD = 3,5cm, BD=5cm và ∠ (DAB) = ∠ (DBC). Sau khi tính, hãy vẽ lại hình chính xác bằng thước và compa.
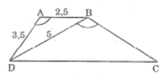
Vẽ hình thang ABCD
- B1: Vẽ tam giác ABD theo độ dài cho trước của mỗi cạnh
- B2: Lấy B làm tâm, quay cung tròn có bán kính 7cm, rồi lấy D làm tâm quay cung tròn có bán kính 10cm, hai cung này cắt nhau tại điểm C ( khác phía với A so với BD)
1) Cho tu giac ABCD co AB=2,5cm; AD=4cm; BD=5cm; BC=8cm; CD=10cm. CMinh ABCD la hinh thang
3) Cho tam giac ABC co AB=4cm, D thuoc AC, AD=2cm, DC=6cm. Biet goc A=100, goc B-C=20. Tinh goc ABD
Cho hình thang ABCD ( AB//CD ). Biết ab = 2,5cm, AD = 3,5cm, BD = 5cm và góc DAB = góc DBC
a) CM tam giác ADB đồng dạng với tam giác BCD
b) Tính BC và CD
c) Tính tỉ số diện tích tam giác ADB và BCD
a) Xét 2 tam giác ADB và BCD có: góc DAB = góc DBC (gt) góc ABD = góc BDC ( so le trong ) nên tam giác ADB đồng dạng với tam giác BDC.(1) b) Từ (1) ta được AB/BC = DB/CD = AB/BD hay ta có; AD/BC = AB/BD <==> 3,5/BC = 2,5/5 ==> BC= 3,5*5/2,5 = 7 (cm) ta cũng có: DB/CD = AB/BD <==> 5/CD = 2,5/5 ==> CD = 5*5/2,5 =10 (cm) c) Từ (1) ta được; AD/BC = DB/CD = AB/BD hay 3.5/7 = 5/10 = 2,5/5 = 1/2 . ta nói tam giác ADB đồng giạc với tam giác BCD theo tỉ số đồng dạng là 1/2 mà tỉ số diện tích bằng bình phương tỉ số động dạng do đó S ADB/ S BCD = (1/2)^2 = 1/4
Bài 3: Cho hình thang ABCD(AB //CD). Biết AB = 2,5cm; AD = 3,5cm; BD = 5cm; và góc
DAB = DBC.
a) Chứng minh hai tam giác ADB và BCD đồng dạng.
b) Tính độ dài các cạnh BC và CD.
c) Tính tỉ số diện tích hai tam giác ADB và BCD.
Bài 4:Cho tam giác vuông ABC vuông ở A ; có AB = 8cm; AC = 15cm; đường cao AH
a) Tính BC; BH; AH.
b) Gọi M,N lần lượt là hình chiếu của H lên AB và AC.Tứ giác AMNH là hình gì? Tính độ dài đoạn MN.
c) Chứng minh AM.AB = AN.AC.