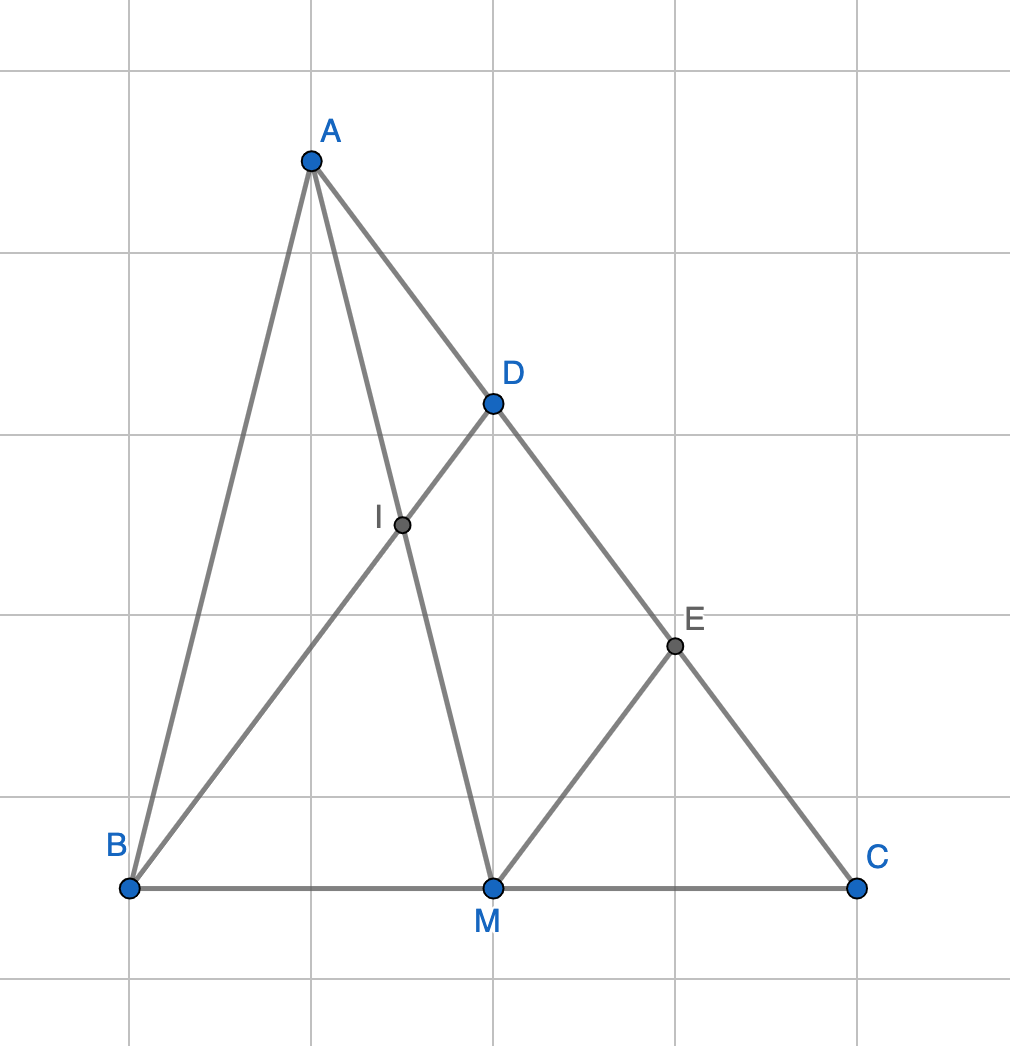
Chp tam giác ABC, trung tuyến AM. Gọi I là trung điểm của AM, D là giao điểm của CI và AB, E là trung điểm của BD.
a) Chứng minh: DA = \(\frac{1}{2}\)DB
b) Chứng minh DI \(\frac{1}{4}\) DC.
Giúp e với ạ! Thanks
Những câu hỏi liên quan
Cho tam giác ABC, trung tuyến AM. Gọi I là trung điểm của AM, D là giao điểm của CI và AB, E là trung điểm của BD.
a) Chứng minh: DA = \(\frac{1}{2}\)DB
b) Chứng minh DI = \(\frac{1}{4}\) DC.
Giúp e với ạ! Thanks
Cho tam giác ABC, trung tuyến AM. Gọi I là trung điểm của AM, D là giao điểm của CI và AB, E là trung điểm của BD.
a) Chứng minh: DA = \(\frac{1}{2}\)DB
b) Chứng minh DI = \(\frac{1}{4}\) DC.
Giúp e với ạ! Thanks
Cho tam giác ABC, trung tuyến AM. Gọi I là trung điểm AM, D là giao điểm của CI và AB. E là trung điểm BD.
a/ CMR: DA=\(\frac{1}{2}\)DB
b/ CMR: DI=\(\frac{1}{4}\)DC
Cho tam giác ABC, đường trung tuyến AM, điểm I thuộc đoạn AM. Gọi E là giao điểm của BI và AC, F là giao điểm của CI và AB. Chứng minh EF song song với BC.
4) Cho AM là đường trung tuyến tam giác ABC .Trên đoạn AB lấy 2 điểm D và E sao cho
AD=DE = EB .Gọi I là giao điểm của CD với AM . Chứng minh : AI = IM và DC = 4 DI
Xét ΔBDC có
E là trung điểm của BD(gt)
M là trung điểm của BC(gt)
Do đó: EM là đường trung bình của ΔBDC(Định nghĩa đường trung bình của tam giác)
Suy ra: EM//DC và \(EM=\dfrac{DC}{2}\)(Định lí 2 về đường trung bình của tam giác)
hay DI//EM
Xét ΔAEM có
D là trung điểm của AE(gt)
DI//EM(cmt)
Do đó: I là trung điểm của AM(Định lí 1 về đường trung bình của tam giác)
Suy ra: AI=IM
Xét ΔAEM có
D là trung điểm của AD(gt)
I là trung điểm của AM(cmt)
Do đó: DI là đường trung bình của ΔAEM(Định nghĩa đường trung bình của tam giác)
Suy ra: \(DI=\dfrac{EM}{2}\)(Định lí 2 về đường trung bình của tam giác)
\(\Leftrightarrow EM=2\cdot DI\)
\(\Leftrightarrow DC\cdot\dfrac{1}{2}=2\cdot DI\)
hay DC=4DI(Đpcm)
Đúng 2
Bình luận (0)
Xét ΔBDC có
E là trung điểm của BD(gt)
M là trung điểm của BC(gt)
Do đó: EM là đường trung bình của ΔBDC(Định nghĩa đường trung bình của tam giác)
Suy ra: EM//DC và DI=EM2DI=EM2(Định lí 2 về đường trung bình của tam giác)
⇔EM=2⋅DI⇔EM=2⋅DI
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A, có đường trung tuyến AM. Gọi D là trung điểm của AB, E là trung điểm đối xứng với M qua D
a chứng minh tứ giác AEBM là hình thoi
b, gọi I là trung điểm của AM. Chứng minh E,I,C thẳng hàng
c, tam giác ABC có thêm điều kiện gì thì AEBM là hình vuông
a: Xét tứ giác AEBM co
D là trung điểm chung của AB và ME
MA=MB
DO đó: AEBM là hình thoi
b: Xét tứ giác AEMC có
AE//MC
AE=MC
Do đó: AEMC là hình bình hành
=>AM cắt EC tại trung điểm của mỗi đường
=>E,I,C thẳng hàng
c: Để AEBM là hình vuông thì góc AMB=90 độ
=>AM vuông góc với BC
=>ΔABC cân tại A
=>AB=AC
Đúng 1
Bình luận (0)
Cho tam giác ABC, trung tuyến AM . Lấy D trên AC sao cho DA= \(\dfrac{1}{2}\)DC .Gọi I là giao điểm của AM và DB , gọi E là trung điểm DC
a, chứng minh AD=DE=EC
b, Chứng minh DEMB là hình thang
C, Chứng minh IA=IM
a) Ta có: \(AD=\dfrac{1}{2}DC\)(gt)
mà \(EC=ED=\dfrac{DC}{2}\)(E là trung điểm của DC)
nên AD=EC=ED
b) Xét ΔCDB có
M là trung điểm của BC(gt)
E là trung điểm của CD(gt)
Do đó: ME là đường trung bình của ΔCDB(Định nghĩa đường trung bình của tam giác)
Suy ra: ME//BD và \(ME=\dfrac{1}{2}BD\)(Định lí 2 về đường trung bình của tam giác)
hay ME//ID
Xét tứ giác MEDB có ME//BD(cmt)
nên MEDB là hình thang có hai đáy là ME và BD(Định nghĩa hình thang)
c) Xét ΔAME có
D là trung điểm của AE(AD=DE, D nằm giữa A và E)
DI//ME(cmt)
Do đó: I là trung điểm của AM(Định lí 1 về đường trung bình của tam giác)
hay IA=IM(Đpcm)
Đúng 2
Bình luận (0)
\(a.\) Ta có: DA=\(^{\dfrac{1}{2}DC=DE=EC}\) (đpcm)
\(b.\) Xét tam giác DBC có:
\(\left\{{}\begin{matrix}DE=CE\\BM=CM\end{matrix}\right.\) \(\Rightarrow\) ME là đường trung bình tam giacs DBC
\(\Rightarrow ME\)//\(BD\) \(\Rightarrow\) DEMB là hình thang
\(c.\)Vì \(\Rightarrow ME\)//\(BD\) nên ME // ID
Xét tam giác AMD có: \(\left\{{}\begin{matrix}ME\backslash\backslash ID\\AD=DC\end{matrix}\right.\)
=> ME là đường trung bình tam giác AMD hay I là trung điểm MA
\(\Rightarrow IA=IM\) (đpcm)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Bài 4.Cho tam giác ABC, đường trung tuyến AM. Gọi D là trung điểm của AM, E là giao điểm của BD và AC. Chứng minh AE = 1/2 EC
Gọi K là trung điểm của EC
Xét ΔBEC có
M là trung điểm của BC(gt)
K là trung điểm của EC(Gt)
Do đó: MK là đường trung bình của ΔBEC
Suy ra: MK//BE
hay MK//DE
Xét ΔAMK có
D là trung điểm của AM(Gt)
DE//MK(cmt)
Do đó: E là trung điểm của AK(Định lí 1 đường trung bình của tam giác)
Suy ra: AE=EK
mà EK=KC
nên AE=EK=KC
\(\Leftrightarrow AE=\dfrac{EK+KC}{2}=\dfrac{EC}{2}\)
Đúng 1
Bình luận (2)
Cho tam giác ABC có đương trung tuyến AM gọi K là giao điểm của CI và AB. Laya I là trung điểm của AB.P là giao của BI và AC. Chứng minh
a,ak=1/2bk;ap=1/2cp
b,gọi e và f là giao cua BI và CI , U và V là trung điểm của Pk và CP. Chứng minh M;E;U và M; F;P thẳng hàng
c, tính chu vi tứ giác MEIF biết AB=6cm;AC=8cm