Cho 1 tam giác bằng giấy, dùng kéo cắt nó thành 3 tam giác nhỏ. Lấy 1 trong các tam giác nhỏ cắt ra thành 3 tam giác nhỏ nữa. Cứ làm như vậy mãi, có bao giờ cắt được 2016 tam giác đó hay không ? Vì sao ?

Những câu hỏi liên quan
Ai có thể giải nhanh giúp mk vs:
cho tam giác bằng giấy, dùng kéo cắt thành 3tam giac nhỏ. Lấy 1 trong các tam giác nhỏ cắt thành 3tam giác nhỏ hơn nữa. Cứ làm như vậy mãi hỏi cắt dược 2016 tam giác nhỏ ko? Vì sao?
ko.vì nếu cắt đc 2016 tam giác nhỏ thì có mà mịn như hạt cát ý
Đúng 0
Bình luận (0)
Dùng kéo cắt một tờ giấy thành hình tam giác ABC. Đặt tam giác lên tờ giấy thứ hai. Vẽ và cắt theo các cạnh của tam giác ABC thành tam giác A’B’C’ (Hình 1). Hãy so sánh các cạnh và các góc của hai tam giác ABC và A’B’C’.
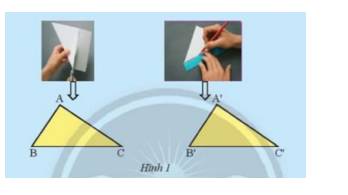
Ta thấy 2 tam giác có các cặp góc bằng nhau \(\widehat A = \widehat {A'}\); \(\widehat B = \widehat {B'}\); \(\widehat C = \widehat {C'}\)
2 tam giác có các cặp cạnh bằng nhau AC = A’C’; AB = A’B’; BC = B’C’
Đúng 0
Bình luận (0)
Có 1 miếng bìa hình tam giác , lần thứ nhất dùng kéo cắt 3 góc ở đỉnh theo đường thẳng để được 1 hình đa giác (phần cắt bỏ đi là tam giác ) . Lại lấy kéo cắt tất cả các góc ở đỉnh đa giác (ở lần cắt 1) theo đường thẳng . Tiếp tục cắt như vậy ... Hỏi sau 4 lần cắt ta được hình đa giác có bao nhiêu cạnh ?
Một đa giác lồi \(n\) cạnh được chia thành các tam giác bằng cách vẽ \(n-3\) đường chéo đôi một không cắt nhau ở bên trong đa giác. Biết rằng ở mỗi đỉnh có một số lẻ các tam giác nhỏ. CMR \(n⋮3\)
Để chứng minh rằng một đa giác lồi có n cạnh, khi được chia thành các tam giác bằng nhau bằng cách vẽ n-3 đường chéo đôi một không cắt nhau, thì n phải chia hết cho 3, ta có thể sử dụng phương pháp quy nạp (induction) để giải quyết bài toán này.
Đầu tiên, chúng ta xét trường hợp đơn giản nhất khi n = 3, tức là đa giác là tam giác. Trong trường hợp này, không cần vẽ đường chéo nào cả, vì tam giác đã được chia thành các tam giác bằng nhau. Và n = 3 chia hết cho 3.
Giả sử đa giác có n cạnh thỏa mãn điều kiện trong đề bài. Ta sẽ chứng minh rằng khi thêm một cạnh mới vào đa giác, tức là n+1 cạnh, thì n+1 cũng phải chia hết cho 3.
Giả sử đa giác có n cạnh và đã được chia thành các tam giác bằng nhau bằng cách vẽ n-3 đường chéo đôi một không cắt nhau. Khi thêm một cạnh mới vào đa giác, chúng ta sẽ thêm một tam giác mới và tạo ra một đường chéo mới. Khi đó, số tam giác trong đa giác tăng thêm một đơn vị và số đường chéo tăng thêm một đơn vị.
Điều quan trọng là ta phải đảm bảo rằng khi thêm một cạnh mới vào, chúng ta vẫn có thể chia đa giác thành các tam giác bằng nhau bằng cách vẽ n-2 đường chéo đôi một không cắt nhau. Điều này có nghĩa là ta cần thêm một đường chéo mới để duy trì tính chất của đa giác ban đầu.
Với việc thêm một cạnh mới, số đường chéo tăng lên một đơn vị, nên ta cần có (n-2)+1 = n-1 đường chéo. Điều này đồng nghĩa với việc n-1 phải chia hết cho 3.
Dựa trên quy nạp, chúng ta có thể kết luận rằng với mọi số tự nhiên n ≥ 3, nếu đa giác có n cạnh và được chia thành các tam giác bằng nhau bằng cách vẽ n-3 đường chéo đôi một không cắt nhau, thì n phải chia hết cho 3.
Vậy, điều phải chứng minh đã được chứng minh.
Đúng 1
Bình luận (0)
Có 1 miếng bìa hình tam giác , lần thứ nhất dùng keeos cắt 3 góc ở đỉnh theo đường thẳng để được 1 hình đa giác (phần cắt bỏ đi là tam giác ) . Lại lấy kéo cắt tất cả các góc ở đỉnh đa giác (ở lần cắt 1) theo đường thẳng . Tiếp tục cắt như vậy ... Hỏi sau 4 lần cắt ta được hình đa giác có bao nhiêu cạnh ?
a) Có thể dùng kéo cắt 2 lầ và chỉ cắt theo đường thẳng chia một tam giác (thường) thành ba mảnh đê rghesp lại được một hình chữ nhật hay không ?
Từ đó suy ra công thức tính diện tích tam giác thường dựa vào công thức tính diện tích hình chữ nhật
b) Hãy chia một tam giác thành 2 phần có diện tích bằng nhau bởi một đường thẳng đi qua đỉnh của tam giác đó
c) Hãy chia một tam giác thành 4 phần có diện tích bằng nhau bởi ba đường thẳng, trong đó chỉ có một đường đi qua đỉnh của tam giác đó
Đọc tiếp
a) Có thể dùng kéo cắt 2 lầ và chỉ cắt theo đường thẳng chia một tam giác (thường) thành ba mảnh đê rghesp lại được một hình chữ nhật hay không ?
Từ đó suy ra công thức tính diện tích tam giác thường dựa vào công thức tính diện tích hình chữ nhật
b) Hãy chia một tam giác thành 2 phần có diện tích bằng nhau bởi một đường thẳng đi qua đỉnh của tam giác đó
c) Hãy chia một tam giác thành 4 phần có diện tích bằng nhau bởi ba đường thẳng, trong đó chỉ có một đường đi qua đỉnh của tam giác đó
Đường tròn (O;R) nội tiếp tam giác ABC. Các tiếp tuyến với đường tròn (O) song song với các cạnh của tam giác ABC cắt từ tam giác ABC thành ba tam giác nhỏ. Gọi r1,r2,r3�1,�2,�3 lần lượt là bán kính các đường tròn nội tiếp tam giác nhỏ đó. Chứng minh rằng: r1+r2+r3r
Đọc tiếp
Đường tròn (O;R) nội tiếp tam giác ABC. Các tiếp tuyến với đường tròn (O) song song với các cạnh của tam giác ABC cắt từ tam giác ABC thành ba tam giác nhỏ. Gọi lần lượt là bán kính các đường tròn nội tiếp tam giác nhỏ đó. Chứng minh rằng:
Đố vui :
a) Có thể dùng kéo cắt 1 lần và chỉ cắt theo đường thẳng, chia một hình chữ nhật thành hai mảnh để ghép lại được 1 tam giác vuông hay không ?
b) Có thể dùng kéo 2 lần và chỉ cắt theo đường thẳng, chia một hình chữ nhật thành 3 mảnh để ghép lại được một tam giác thường hay không ?
Cắt một hình vuông thành 3 hình tam giác thỏa mãn tổng diện tích tam giác của 2 tam giác nhỏ cộng lại bằng diện tích tam giác còn lại và 3 hình ghép lại thành một tam giác.
Thời gian còn lại để 12 người đó xây xong ngôi nhà là:
40 - 10 = 30 (ngày)
3 người nữa đến cùng làm thì số người đến xây nhà là:
12 + 3 = 15 (người)
Thời gian 15 người đó xây xong ngôi nhà là:
12 x 40 : 15 = 24 (ngày)
Đáp số: 24 ngày
Đúng 0
Bình luận (0)
Thời gian còn lại để 12 người đó xây xong ngôi nhà là:
40 - 10 = 30 (ngày)
3 người nữa đến cùng làm thì số người đến xây nhà là:
12 + 3 = 15 (người)
Thời gian 15 người đó xây xong ngôi nhà là:
12 x 40 : 15 = 24 (ngày)
Đáp số: 24 ngày
Đúng 0
Bình luận (0)



















