Cho em xin lời giải ạ !

Những câu hỏi liên quan
Mn cho em xin lời giải bài này ạ..... Em cảm ơn mn nhiều ạ

\(y'=-3mx^2+2x-3\)
Hàm nghịch biến trên khoảng đã cho khi với mọi \(x\in\left(-3;0\right)\) ta có:
\(-3mx^2+2x-3\le0\)
\(\Leftrightarrow2x-3\le3mx^2\)
\(\Leftrightarrow\dfrac{2x-3}{3x^2}\le m\)
\(\Rightarrow m\ge\max\limits_{\left(-3;0\right)}\left(\dfrac{2x-3}{3x^2}\right)\)
Xét hàm \(f\left(x\right)=\dfrac{2x-3}{3x^2}\Rightarrow f'\left(x\right)=\dfrac{2\left(3-x\right)}{3x^3}< 0;\forall x\in\left(-3;0\right)\)
\(\Rightarrow f\left(x\right)>f\left(-3\right)=-\dfrac{1}{3}\)
\(\Rightarrow m\ge-\dfrac{1}{3}\)
Đúng 1
Bình luận (0)
Cho em xin lời giải bài này ạ!!! Em cảm ơn ![]()
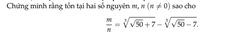
Đặt \(x=\sqrt[3]{\sqrt[]{50}+7}-\sqrt[3]{\sqrt[]{50}-7}\)
\(x^3=14-3\sqrt[3]{\left(\sqrt[]{50}+7\right)\left(\sqrt[]{50}-7\right)}\left(\sqrt[3]{\sqrt[]{50}+7}-\sqrt[3]{\sqrt[]{50}-7}\right)\)
\(x^3=14-3x\)
\(x^3+3x-14=0\)
\(\left(x-2\right)\left(x^2+2x+7\right)=0\)
\(x=2\)
\(\Rightarrow\dfrac{m}{n}=2\)
\(\Rightarrow\) Hiển nhiên tồn tại vô số m, n nguyên thỏa mãn đẳng thức trên
Đúng 0
Bình luận (0)
Mọi người cho em xin lời giải ạ
Đọc tiếp
Mọi người cho em xin lời giải ạ
Cho em xin lời giải chi tiết ạ

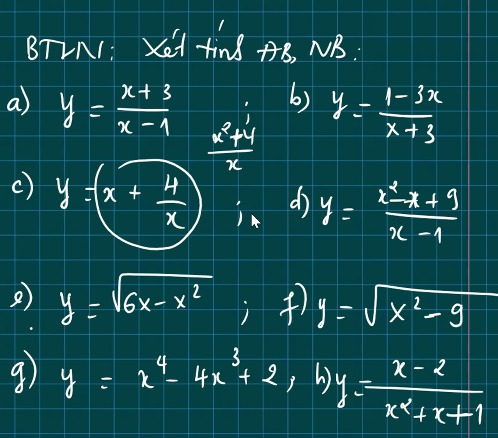 Cho em xin lời giải chi tiết với ạ
Cho em xin lời giải chi tiết với ạ
f.
TXĐ: \(x\in(-\infty;-3]\cup[3;+\infty)\)
\(y'=\dfrac{2x}{2\sqrt{x^2-9}}=\dfrac{x}{\sqrt{x^2-9}}\)
Dấu của y':

Hàm đồng biến trên \([3;+\infty)\) và nghịch biến trên \((-\infty;-3]\)
g.
\(y'=4x^3-12x^2=4x^2\left(x-3\right)=0\Rightarrow x=3\) (khi tìm khoảng đơn điệu hay cực trị của hàm số thì chỉ cần quan tâm nghiệm bội lẻ, không cần quan tâm nghiệm bội chẵn)
Dấu của y':
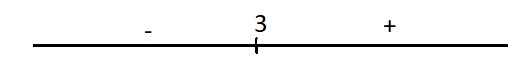
Hàm đồng biến trên \(\left(3;+\infty\right)\) và nghịch biến trên \(\left(-\infty;3\right)\)
h.
\(y'=\dfrac{x^2+x+1-\left(x-2\right)\left(2x+1\right)}{\left(x^2+x+1\right)^2}=\dfrac{-x^2+4x+3}{\left(x^2+x+1\right)^2}\)
\(y'=0\Leftrightarrow-x^2+4x+3=0\Rightarrow\left[{}\begin{matrix}x=2-\sqrt{7}\\x=2+\sqrt{7}\end{matrix}\right.\)
Dấu của y':
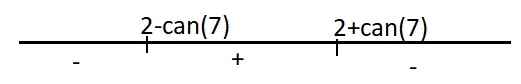
Hàm đồng biến trên \(\left(2-\sqrt{7};2+\sqrt{7}\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;2-\sqrt{7}\right)\) và \(\left(2+\sqrt{7};+\infty\right)\)
Đúng 0
Bình luận (0)
Cho em xin lời giải phầm a và b ạ em cảm ơn 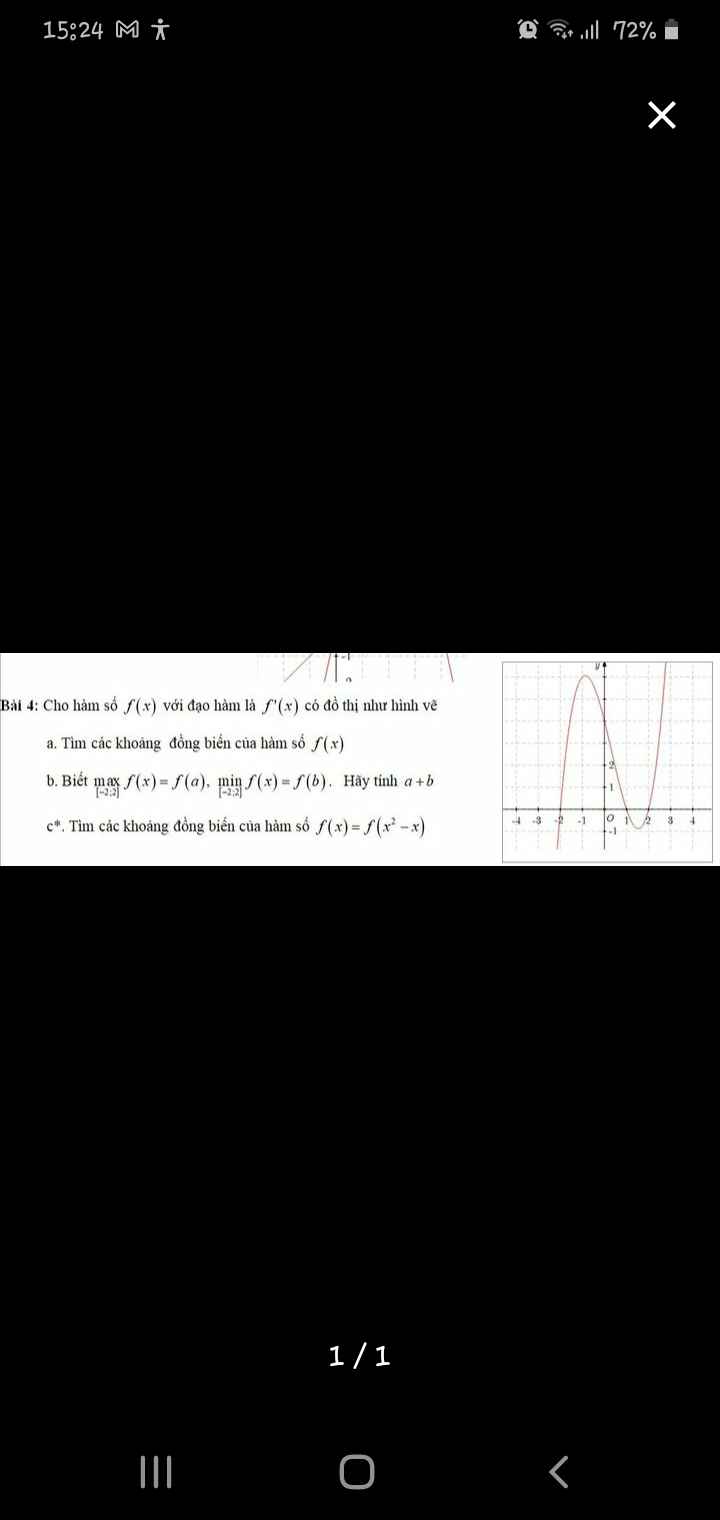
Từ đồ thị \(f'\left(x\right)\) ta có BBT hàm \(f\left(x\right)\) như sau:
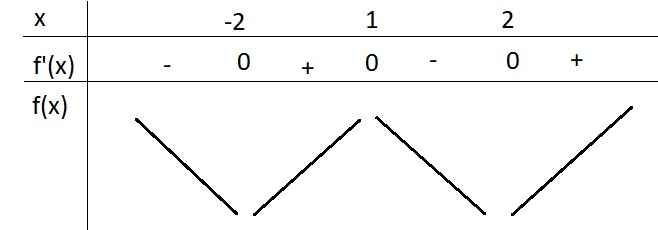
Từ đó ta thấy hàm \(f\left(x\right)\) đồng biến trên các khoảng \(\left(-2;1\right)\) và \(\left(2;+\infty\right)\)
Cũng từ BBT, trên \(\left[-2;2\right]\) ta thấy \(\max\limits_{\left[-2;2\right]}f\left(x\right)=f\left(1\right)\)
Diện tích giới hạn bởi phần đồ thị \(f'\left(x\right)\) và trục hoành trên \(\left[-2;1\right]\) lớn hơn đoạn \(\left[1;2\right]\)
\(\Rightarrow\int\limits^1_{-2}\left|f'\left(x\right)\right|dx>\int\limits^2_1\left|f'\left(x\right)\right|dx\Rightarrow\int\limits^1_{-2}f'\left(x\right)dx>\int\limits^1_2f'\left(x\right)dx\)
\(\Rightarrow f\left(1\right)-f\left(-2\right)>f\left(1\right)-f\left(2\right)\)
\(\Rightarrow f\left(2\right)>f\left(-2\right)\)
\(\Rightarrow\min\limits_{\left[-2;2\right]}f\left(x\right)=f\left(-2\right)\)
\(\Rightarrow a+b=1+\left(-2\right)=-1\)
Đúng 1
Bình luận (0)
M.n cho e xin lời giải chi tiết câu 6,7,8,9,10,11,12,13,14,15 ạ em cảm ơn ạ 
để nhận được câu trả lời nhanh và chi tiết thì bạn vui lòng chia nhỏ ra để đăng nhé! Mỗi lần chỉ nên đăng 1 - 2 câu thôi!
Đúng 1
Bình luận (0)
thầy cô cho em xin lời giải cho tiết c1,c3 ạ
Mong mng cho em lời giải chi tiết
Em xin cảm ơn nhiều ạ 
\(n_{Fe}=\dfrac{5,6}{56}=0,1mol\)
\(n_S=\dfrac{4,8}{32}=0,15mol\)
\(Fe+S\underrightarrow{t^o}FeS\)
0,1 0,15 0,1
\(FeS+2HCl\rightarrow FeCl_2+H_2S\uparrow\)
0,1 0,1 0,1
\(V_Y=0,1\cdot22,4=2,24l\)
\(m_Z=m_{FeCl_2}=0,1\cdot127=12,7g\)
Đúng 3
Bình luận (1)
















