cho tam giác DEF cân tại D. Kẻ DH vuông góc với EF ( H ∈ EF ) . Chứng minh rằng :
a/ HE=HF
B/ DEH=DFH
Ghi lời giải giúp mik nhé!
Cho tam giác DEF cân tại D,H là trung điểm EF
a)Chứng minh tam giác DEH = tam giác DFH
b)Chứng minh DH vuông góc với EF
c)Trên tia DH lấy điểm K sao cho HD = HK.Chứng minh với FK
`a,` Xét Tam giác `DEH` và Tam giác `DFH` có:
`DE=DF (\text {Tam giác ABC cân tại A})`
`\widehat{DEF}=\wide{DFE} (\text {Tam giác ABC cân tại A})`
`HE=HF (g``t)`
`=> \text {Tam giác DEH = Tam giác DFH (c-g-c)}`
`b, \text {Vì Tam giác DEH = Tam giác DFH (a)}`
`-> \widehat{DHE}= \widehat{DHF} (\text {2 góc tương ứng})`
`\text {Mà 2 góc này nằm ở vị trí đồng vị}`
`->\widehat{DHE}+ \widehat{DHF}=180^0`
`-> \widehat {DHE}= \wideha{DHF}=180/2=90^0`
`-> DH \bot EF`
`c,` Mình xp sửa đề là: \(\text{"Trên tia ĐỐI của DH lấy điểm K sao cho HD=HK"}\)
Xét Tam giác `DHE` và Tam giác `FHK` có:
`DH=HK (g``t)`
`\widehat{DHE}=\widehat{FHK} (\text {2 góc đối đỉnh})`
`HE=HF (g``t)`
`=> \text {Tam giác DHE = Tam giác FHK (c-g-c)}`
`-> \widehat{DEF}=\widehat{EFK} (\text {2 góc tương ứng})`
`\text {Mà 2 góc này nằm ở vị trí sole trong}`
`-> DE`//`FK (\text {tính chất đt' song song})`
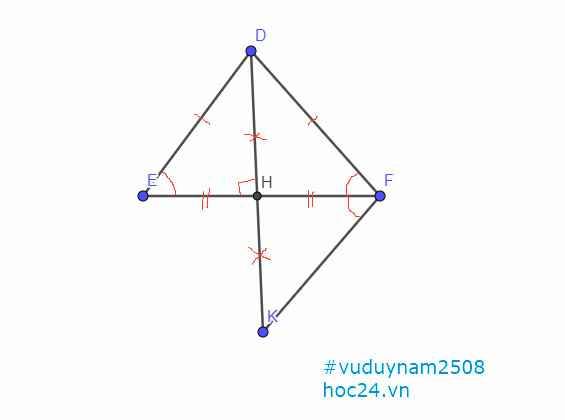
Cho tam giác DEF cân tại D,H là trung điểm EF
a)Chứng minh tam giác DEH = tam giác DFH
b)Chứng minh DH vuông góc với EF
c)Trên tia DH lấy điểm K sao cho HD = HK.Chứng minh DE // với FK
Cho tam giác DEF cân tại D. Gọi H là trung điểm của EF. a) C/m: t/giác DEH = t/giác DFH và DH vuông góc EF b) Kẻ HM vuông góc DE tại M, HN vuông góc DF tại N. C/m: t/giác HMN cân tại H c) C/m: MN// EF d) Qua E kẻ đường thẳng d vuông góc với DE, qua F kẻ đường thẳng d' vuông góc với DF, đường thẳng d cắt đường thẳng d' tại K. C/m: D, H , K thẳng hàng.
a) Xét tam giác DEH và tam giác DFH ta có:
DE = DF ( tam giác DEF cân tại D )
DEH = DFH ( tam giác DEF cân tại D )
EH = EF ( H là trung điểm của EF )
=> tam giác DEH = tam giác DFH ( c.g.c) (dpcm)
=> DHE=DHF(hai góc tương ứng)
Mà DHE+DHF=180 độ =>DHE=DHF=180 độ / 2 = 90 độ ( góc vuông ) hay DH vuông góc với EF ( dpcm )
b) Xét tam giác MEH và tam giac NFH ta có:
EH=FH(theo a)
MEH=NFH(theo a)
=> tam giác MEH = tam giác NFH ( ch-gn)
=> HM=HN ( 2 cạnh tương ứng ) hay tam giác HMN cân tại H ( dpcm )
c) Ta có : +) DM+ME=DE =>DM=DE-ME
+) DN+NF=DF => DN=DF-NF
Mà DE=DF(theo a) ; ME=NF( theo b tam giác MEH=tam giác NFH)
=>DM=DN => tam giác DMN cân tại D
Xét tam giac cân DMN ta có:
DMN=DNM=180-MDN/2 (*)
Xét tam giác cân DEF ta có:
DEF=DFE =180-MDN/2 (*)
Từ (*) và (*) Suy ra góc DMN = góc DEF
Mà DMN và DEF ở vị trí đồng vị
=> MN//EF (dpcm)
d) Xét tam giác DEK và tam giác DFK ta có:
DK là cạnh chung
DE=DF(theo a)
=> tam giác DEK= tam giác DFK(ch-cgv)
=>DKE=DKF(2 góc tương ứng)
=>DK là tia phân giác của góc EDF (1)
Theo a tam giac DEH= tam giac DFH(c.g.c)
=>EDH=FDH(2 góc tương ứng)
=>DH là tia phân giác của góc EDF (2)
Từ (1) và (2) Suy ra D,H,K thẳng hàng (dpcm)
Cho tam giác DEF cân tại D. Gọi N và M lần lượt là trung điểm của DE và DF kẻ DH vuông góc EF tại H.
a. Chứng minh: HE = HF
b. Cho DE = DF = 5cm; EF = 6cm. Tính DH?
c. Chứng minh Góc DEM = góc DFN?
d. Gọi K là trung điểm MN. Chứng minh: D, H, K thẳng hàng?
a: Ta có: ΔDEF cân tại D
mà DH là đường cao
nên H là trung điểm của EF
hay EH=FH
b: EH=FH=EF/2=3(cm)
Xét ΔDHE vuông tại H có \(DE^2=DH^2+HE^2\)
nên DH=4(cm)
c: Xét ΔDEM và ΔDFN có
DE=DF
\(\widehat{EDM}\) chung
DM=DN
Do đó: ΔDEM=ΔDFN
Suy ra: \(\widehat{DEM}=\widehat{DFN}\)
d: Xét ΔNEH và ΔMFH có
NE=MF
\(\widehat{E}=\widehat{F}\)
EH=FH
Do đó: ΔNEH=ΔMFH
Suy ra: HN=HM
hay H nằm trên đường trung trực của MN(1)
Ta có: KM=KN
nên K nằm trên đường trung trực của MN(2)
Ta có: DN=DM
nên D nằm trên đường trung trực của MN(3)
Từ (1), (2) và (3) suy ra D,H,K thẳng hàng
a. xét tam giác DHE và tam giác DHF, có:
D: góc chung
DE = DF ( DEF cân )
DH: cạnh chung
Vậy tam giác DHE = tam giác DHF ( c.g.c )
=> HE = HF ( 2 cạnh tương ứng )
b.ta có: EH = EF :2 ( EF là đường cao cũng là trung tuyến ) = 6 : 2 =3 cm
áp dụng định lý pitago vào tam giác vuông DHE, có:
\(DE^2=DH^2+EH^2\)
\(\Rightarrow DH=\sqrt{DE^2-EH^2}=\sqrt{5^2-3^2}=\sqrt{16}=4cm\)
c.xét tam giác DEM và tam giác DFN có:
DE = DF ( DEF cân )
DM = DN ( gt )
D: góc chung
Vậy tam giác DEM = tam giác DFN ( c.g.c )
=> góc DEM = góc DFN ( 2 góc tương ứng )
d.xét tam giác DKM và tam giác DKN, có:
DM = DN ( gt )
D: góc chung
DK: cạnh chung
Vậy tam giác DKM = tam giác DKN ( c.g.c )
=> góc DKM = góc DKN = 90 độ ( tam giác BNM cân, K là trung điểm cũng là đường cao )
=> DK vuông BC
Mà DH cũng vuông BC
=> D,H,K thẳng hàng
Chúc bạn học tốt!!!
cho tam giác DEF cân tại D. Gọi N và M lần lượt là trung điểm của DE và DF,kẻ DH vuông góc với EF tại H.
A)chứng minh HE = HF
B)cho DE =DF = 5cm,EF = 6cm.Tính độ dài đoạn DH
C)chứng minh DEM = DFN
D)gọi K là trung điểm của MN. Chứng minh ba điểm D,K,H cùng nằm trên 1 đường thẳng
cho tam giác DEF cân tại D vẽ DH vuông góc EF tại H
a/ chứng minh tam giác DEH = tam giác DFH. Suy ra H là trung điểm của EF
b/ lấy M ϵ DE, N ϵ DF, sao cho MD = ND. Chứng minh tam giác HMN là tam giác cân
c/ chứng minh MN // EF
d/ Gọi i là trung điểm của MN. Chúng minh D, I, H thẳng hàng
a) xét tam giác DHE và tam giác DHF có
DH chung
DE = DF (gt)
góc DHE = góc DHF (=90 độ)
=> tam giác DHE = tam giác DHF (c.g.c)
=> HE = HF
=> H là trung điểm của EF
b) xét tam giác EMH và tam giác FNH có
HE = HF (cmt)
Góc MEH = góc MFH (gt)
Góc EHM = góc FHM (đối đỉnh)
=> tam giác EMH = tam giác FNH (g.c.g)
=> HM = HN
=> tam giác HMN cân tại H
a: Xét ΔDEH vuông tại H và ΔDFH vuông tại H có
DE=DF
DH chung
=>ΔDEH=ΔDFH
=>EH=FH
=>H là trung điểm của EF
b: Xet ΔDMH và ΔDNH có
DM=DN
góc MDH=góc NDH
DH chung
=>ΔDMH=ΔDNH
=>HM=NH
c: Xet ΔDEF có DM/DE=DN/DF
nên MN//EF
d: ΔDMN cân tại D
mà DI là trug tuyến
nên DI là phân giác của góc EDF
=>D,I,H thẳng hàng
Bài 5: Cho tam giác DEF cân tại D. Kẻ DH vuông góc với EF (H ∈ EF) a) Chứng minh ∆𝐷𝐻𝐸 = ∆𝐷𝐻𝐹 b) Cho biết DE = 5cm, EF = 8cm. Tính DH? c) Từ H kẻ HM DE, HN DF. Chứng minh rằng HM = HN.
a: Xét ΔDHE vuông tại H và ΔDHF vuông tại H có
DE=DF
DH chung
Do đó:ΔDHE=ΔDHF
b: EF=8cm nên HE=4cm
=>DH=3cm
c: Xét ΔDMH vuông tại M và ΔDNH vuông tại N có
DH chung
\(\widehat{MDH}=\widehat{NDH}\)
Do đó:ΔDMH=ΔDNH
Suy ra: HM=HN
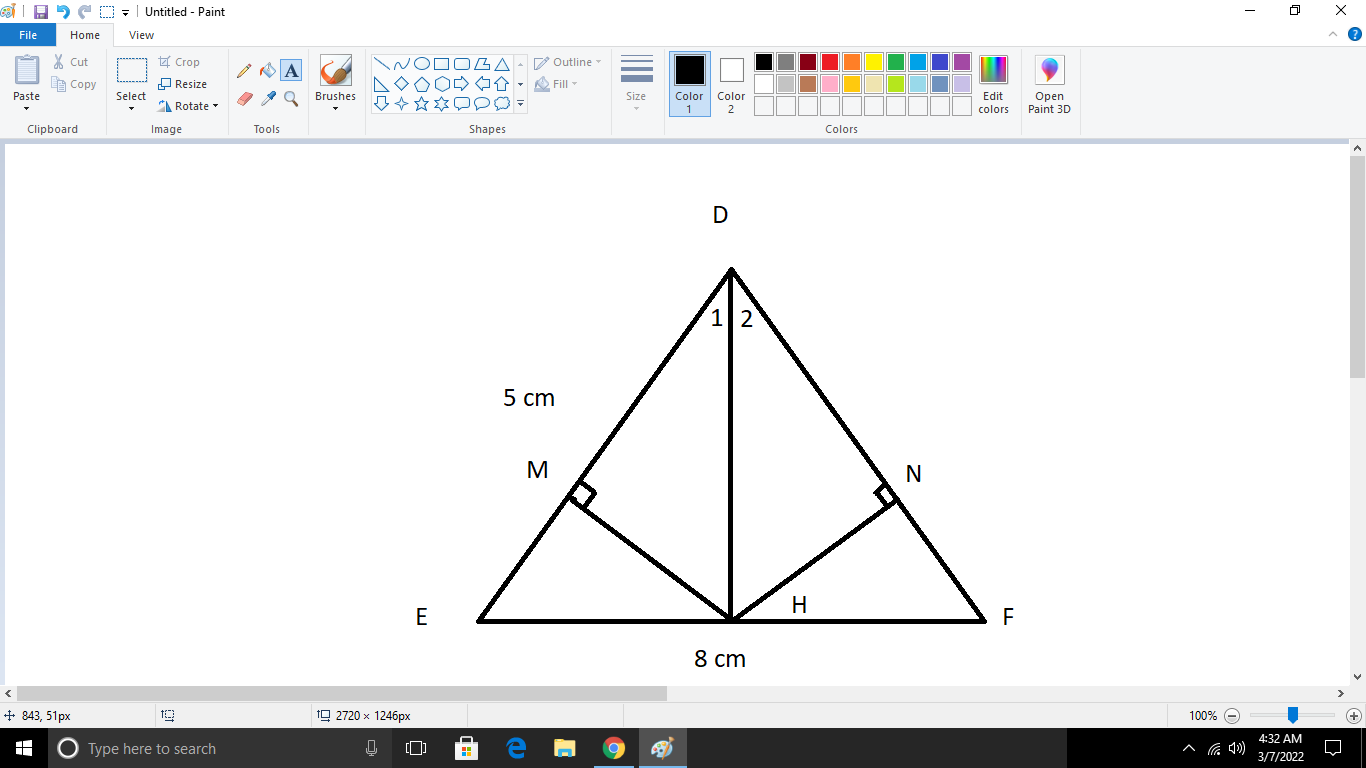
\(\text{a)}\text{Vì }\Delta DEF\text{ cân tại D}\)
\(\Rightarrow DE=DF\)
\(\widehat{E}=\widehat{F}\)
\(\text{Xét }\Delta DHE\text{ và }\Delta AHF\text{ có:}\)
\(DE=DF\left(cmt\right)\)
\(BH\text{ chung}\)
\(\widehat{E}=\widehat{F}\left(cmt\right)\)
\(\Rightarrow\Delta DHE=\Delta DHF\left(c-g-c\right)\)
\(\Rightarrow EH=HF\text{(hai cạnh tương ứng)}\)
\(\text{b)}\text{Vì }EH=HF\left(cmt\right)\)
\(\Rightarrow EH=\dfrac{EF}{2}=\dfrac{8}{2}=4\left(cm\right)\)
\(\text{Xét }\Delta DEH\text{ có:}\)
\(DE^2=DH^2+EH^2\)
\(\Rightarrow DH^2=DE^2-EH^2\text{(định lí Py ta go đảo)}\)
\(\Rightarrow DH^2=5^2-4^2=25-16=9\left(cm\right)\)
\(\Rightarrow DH=\sqrt{9cm}=3\left(cm\right)\)
\(\text{c)Xét }\Delta HMD\text{ và }\Delta HND\text{ có:}\)
\(DH\text{ chung}\)
\(\widehat{D_1}=\widehat{D_2}\left(\Delta DHE=\Delta DHF\right)\)
\(\widehat{DMH}=\widehat{DNH}=90^0\)
\(\Rightarrow\Delta HMD=\Delta HND\left(ch-cgv\right)\)
\(\Rightarrow HM=HN\text{( hai cạnh tương ứng)}\)
Cho tam giác DEF cân tại D. Gọi M,N lần lượt là trung điểm của DF và DE. Kẻ DH vuông góc với EF (H thuộc EF)
a) C/m HE =HF
b) Cho DE=DF=5, EF=6. Tính DH
c) C/m tam giác DME = tam giác DNF. Từ đó suy ra góc DEM = góc DFN
a: Ta có: ΔDEF cân tại D
mà DH là đường cao
nên H là trung điểm của FE
hay HF=HE
b: EF=6cm nên HF=3cm
=>DH=4cm
c: Xét ΔDME và ΔDNF có
DM=DN
\(\widehat{EMD}\) chung
DE=DF
Do đó: ΔDME=ΔDNF
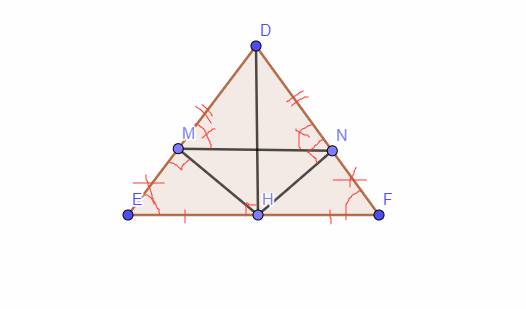
Cho tam giác DEF cân tại D. Kẻ DH vuông góc EF (H thuộc EF) Chứng minh tam giác HED bằng tam giác HFD Kẻ HM vuông góc DE (M thuộc DE) và HN vuông góc DF (N thuộc DF). Chứng minh tam giác DMN cân tại D và MN song song với EF
\(\text{#TNam}\)
`a,` Xét Tam giác `HED` và Tam giác `HFD` có
`DE = DF (\text {Tam giác DEF cân tại D})`
\(\widehat{E}=\widehat{F}\) `(\text {Tam giác DEF cân tại D})`
`=> \text {Tam giác HED = Tam giác HDF (ch-gn)}`
`b,` Vì Tam giác `HED =` Tam giác `HFD (a)`
`-> HE = HF (\text {2 cạnh tương ứng})`
Xét Tam giác `HEM` và Tam giác `HFN` có:
`HE = HF (CMT)`
\(\widehat{E}=\widehat{F}\) `(a)`
\(\widehat{EMH}=\widehat{FNH}=90^0\)
`=> \text {Tam giác HEM = Tam giác HFN (ch-gn)}`
`-> EM = FN (\text {2 cạnh tương ứng})`
Ta có: \(\left\{{}\begin{matrix}DE=MD+ME\\DF=ND+NF\end{matrix}\right.\)
Mà `DE = DF, ME = NF`
`-> MD = ND`
Xét Tam giác `DMN: DM = DN (CMT)`
`-> \text {Tam giác DMN cân tại D}`
`->`\(\widehat{DMN}=\widehat{DNM}=\)\(\dfrac{180-\widehat{A}}{2}\)
Tam giác `DEF` cân tại `D`
`->`\(\widehat{E}=\widehat{F}=\)\(\dfrac{180-\widehat{A}}{2}\)
`->`\(\widehat{DMN}=\widehat{E}\)
Mà `2` góc này nằm ở vị trí đồng vị
`-> \text {MN // EF (t/c 2 đt' //)}`
Bài 10. Cho tam giác DEF vuông tại D, có . Tia phân giác của góc F cắt DE tại I. Kẻ IH vuông góc với EF tại H ( ). a. Chứng minh: DFI = HFI b. DFH là tam giác gì? Vì sao?. c. Qua E kẻ đường thẳng vuông góc với DH tại N. Chứng minh EN // FI. Bài 11. Cho cân ở A. Trên tia đối của các tia BC và CB lấy thứ tự hai điểm D và E sao cho BD = CE. a) Chứng minh cân b) Gọi M là trung điểm của BC. Chứng minh AM là tia phân giác của . c) Từ B và C kẻ BH, CK theo thứ tự vuông góc với AD và AE Chứng minh: BH = CK. d) Chứng minh ba đường thẳng AM, BH, CK đồng quy