tìm các số thực dương x;y;z thỏa mãn điều kiện
\(\int^{x^2+y^2+z^2=4\sqrt{xyz}}_{x+y+z=2\sqrt{xyz}}\)
Cho x, y là các số thực dương thoả mãn x + 1/y = 1. Tìm GTNN của P = x/y + y/x
Em dùng công thức toán học để ghi đề bài sẽ giúp hiểu đúng đề được em nhé.
Cho x y là các số thực dương tm x^2+y^2=9 tìm gtnn của p=3x+y+xy
Cho x,y là các số thực dương TM: x+y=1 Tìm GTNN: \(\dfrac{1}{x^3+y^3}+\dfrac{1}{xy}\)
Bạn xem lại đề bài, mặc dù bài này giải được ra kết quả cụ thể, nhưng chắc không ai cho đề như vậy cả
Sau khi tính toán thì \(P_{min}=4+2\sqrt{3}\)
Dấu "=" xảy ra khi \(\left(x;y\right)=\left(\dfrac{3-\sqrt{6\sqrt{3}-9}}{6};\dfrac{3+\sqrt{6\sqrt{3}-9}}{6}\right)\) và hoán vị
Nhìn thật kinh khủng, chẳng có lý gì cả.
Nếu điều kiện \(x+y=1\) thì biểu thức \(P=\dfrac{a}{x^3+y^3}+\dfrac{b}{xy}\) cần có tỉ lệ \(\dfrac{b}{a}\ge3\) để ra 1 kết quả đẹp mắt và bình thường
Ví dụ có thể cho đề là \(P=\dfrac{1}{3\left(x^3+y^3\right)}+\dfrac{1}{xy}\) hoặc \(P=\dfrac{1}{x^3+y^3}+\dfrac{4}{xy}\) gì đó :)
Cho x, y là các số thực dương thỏa mãn lnx + lny ≥ ln(x2+y) là các số thực dương thỏa mãn P = x + y
A. P = 6
B. P = 2 + 3 2
C. P = 3 + 2 2
D. P = 17 + 3
Đáp án C
Ta có
![]()

Khi đó

![]()
Vậy giá trị nhỏ nhất của biểu thức P là 3 + 2 2
Cho x, y là các số thực dương thỏa mãn ln x + ln y ≥ ln ( x 2 + y ) là các số thực dương thỏa mãn P = x + y
![]()
![]()
![]()
![]()
Tìm Min của:
\(A=\dfrac{1}{x^2+y^2+1}+\dfrac{3}{2xy}\) với x: y là các số thực dương.
Thiếu đề nhé. Giả thiết đang còn có là x+y bé thua hoặc bằng 1
cho các số thực dương x,y thỏa mãn \(xy\ge x+y^2\)
Tìm min của F=x+3y
Mn giúp em với ạ
Viết chương trình nhập số n nguyên dương và dãy số thực B1, B2,... Bn. Và số thực x ( theo C++)
- Xuất dãy vừa nhập;
- Tìm giá trị lớn nhất trong dãy;
- Tính trung bình cộng các phần tử lớn hơn số thực x
#include <bits/stdc++.h>
using namespace std;
double b[100],x,ln,t;
int i,n,dem;
int main()
{
cin>>n;
ln=-1e10;
for (i=1; i<=n; i++)
{
cin>>b[i];
ln=max(ln,b[i]);
}
for (i=1; i<=n; i++)
cout<<b[i]<<" ";
cout<<endl;
cout<<ln<<endl;
t=0;
dem=0;
for (i=1; i<=n; i++)
if (a[i]>x)
{
t=t+a[i];
dem++;
}
cout<<fixed<<setprecision(2)<<t/(dem*1.0);
return 0;
}
Cho các số thực dương x,y. Tìm giá trị lớn nhất của biểu thức P = 4 x y 2 x + x 2 + 4 y 2 3
A. max P=1
B. max P= 1 10
C. max P= 1 8
D. max P= 1 2
Đáp án C
P = 4 x y 2 x + x 2 + 4 y 2 P = 4 y x 2 1 + 1 + 4 y x 2 3
Đặt 1 + 4 y x 2 = t , t ≥ 1 ⇒ 4 y x 2 = t 2 − 1
Ta được hàm:
f ( t ) = t 2 − 1 1 + t 3 = t − 1 1 + t 2 , t ≥ 1 f ' ( t ) = − t 2 + 2 t + 3 1 + t 4 f ' ( t ) = 0 ⇔ t = − 1 ( L ) t = 3
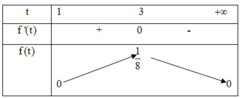
Vậy max P = max [ 1 ; + ∞ ) f ( t ) = 1 8
Cho x, y là các số thực dương thỏa mãn x + \(\dfrac{1}{y}\) = 1. Tìm GTNN của P = \(\dfrac{x}{y}+\dfrac{y}{x}\)