Tìm tất cả các giá trị thực của tham số m để bpt (m+1)x2 -2(m+1)x+4 ≥ 0 có tập nghiệm S=R

Những câu hỏi liên quan
Tìm tất cả các giá trị thực của tham số m để bpt (m+1)x2 -2(m+1)x+4 ≥ 0 có tập nghiệm S=R
TH1: m+1=0 <=> m=-1
Khi đó bpt là -2(-1+1)x+4 >= 0 <=> -4x+4 >= 0 <=> x<=1 (KTM S=R) => loại
TH2: m+1 khác 0 <=> m khác -1
Để bpt (m+1)x2 -2(m+1)x+4 ≥ 0 có nghiệm với mọi x
<=>
<=>
Vậy m>3 thì...
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để bpt (m+1)x2 -2(m+1)x+4 ≥ 0 có tập nghiệm S=R
TH1: m+1=0 <=> m=-1
Khi đó bpt là -2(-1+1)x+4 >= 0 <=> -4x+4 >= 0 <=> x<=1 (KTM S=R) => loại
TH2: m+1 khác 0 <=> m khác -1
Để bpt (m+1)x2 -2(m+1)x+4 ≥ 0 có nghiệm với mọi x
<=> \(\left\{{}\begin{matrix}a>0\\\Delta'\le0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m+1>0\\\left[-\left(m+1\right)\right]^2-4\left(m+1\right)\le0\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}m>-1\\m^2-2m-3\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>-1\\\left[{}\begin{matrix}m< -1\\m>3\end{matrix}\right.\end{matrix}\right.\Leftrightarrow m>3\)
Vậy m>3 thì...
Đúng 1
Bình luận (1)
TH1: m+1=0 <=> m=-1
Khi đó bpt là -2(-1+1)x+4 >= 0 <=> -4x+4 >= 0 <=> x<=1 (KTM S=R) => loại
TH2: m+1 khác 0 <=> m khác -1
Để bpt (m+1)x2 -2(m+1)x+4 ≥ 0 có nghiệm với mọi x
<=>
<=>
Vậy m>3 thì...
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m dể bpt (m+1)x\(^2\)-2(m+1)x+4\(\ge\)0 có tập nghiệm S=R
TH1: m + 1 = 0 <=> m = -1 thay vào bpt ta có: 4 > 0 với mọi số thực x
=> m = - 1 thỏa mãn
TH2: m \(\ne\)-1
bpt có tập nghiệm S = R
<=> \(\hept{\begin{cases}\Delta'\le0\\m+1>0\end{cases}}\Leftrightarrow\hept{\begin{cases}\left(m+1\right)^2-4\left(m+1\right)\le0\\m>-1\end{cases}}\)
<=> \(\hept{\begin{cases}\left(m+1\right)\left(m-3\right)\le0\\m>-1\end{cases}}\Leftrightarrow-1< m\le3\)
Kết hợp 2 TH: ta có: \(-1\le m\le3\) thì bpt có tập nghiệm: S = R
Đặt ( m + 1 ).x2 - 2. ( m-1 ) .x + 4 \(\ge\)0 ( 1 )
+) TH1 : m+ 1 = 0 <=> m =-1 .Bất phương trình ( 1 ) trở thành 4 \(\ge\)0 \(\forall x\inℝ\)( luôn đúng ) ( *)
+) TH2 : m + 1 \(\ne\)0 <=> m \(\ne\)-1 .Bất phương trình ( 1 ) có tập nghiệm \(S=ℝ\)
<=> \(\hept{\begin{cases}a>0\\\Delta'\le0\end{cases}\Leftrightarrow\hept{\begin{cases}m+1>0\\\Delta'=m^2-2m-3\le0\end{cases}\Leftrightarrow}-1< m\le3\left(^∗^∗\right)}\)
Từ ( *) và ( **) ta suy ra : \(-1\le m\le3\)
Tìm tất cả các giá trị thực của tham số m để bất phương trình
(
m
+
1
)
x
2
-
2
(
m
+
1
)
x
+
4
≥
0
(
1
)
có tập nghiệm
S
ℝ
?
A.
m
-
1
B.
-
1
≤...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để bất phương trình ( m + 1 ) x 2 - 2 ( m + 1 ) x + 4 ≥ 0 ( 1 ) có tập nghiệm S = ℝ ?
A. m > - 1
B. - 1 ≤ m ≤ 3
C. - 1 < m ≤ 3
D. - 1 < m < 3
Cho phương trình
m
+
1
log
2
2
x
+
2
log
2
x
+
m
-
2
0
. Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình đã cho có hai nghiệm thực x1, x2 thỏa 0 x1 1 x2 A. ...
Đọc tiếp
Cho phương trình m + 1 log 2 2 x + 2 log 2 x + m - 2 = 0 . Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình đã cho có hai nghiệm thực x1, x2 thỏa 0 < x1 < 1 < x2
A. 2 ; + ∞
B. - 1 ; 2
C. - ∞ ; - 1
D. - ∞ ; - 1 ∪ 2 ; + ∞
Đáp án B.
Đặt t = log2 x,
khi đó m + 1 log 2 2 x + 2 log 2 x + m - 2 = 0
⇔ m + 1 t 2 + 2 t + m - 2 = 0 (*).
Để phương trình (*) có hai nghiệm phân biệt
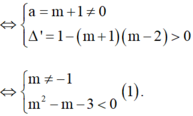
Khi đó gọi x1, x2 lần lượt hai nghiệm của phương trình (*).
Vì 0 < x1 < 1 < x2 suy ra
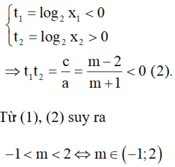
Đúng 0
Bình luận (0)
Cho phương trình
m
+
1
log
2
2
x
+
2
log
2
x
+
(
m
-
2
)
0
. Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình đã cho có hai nghiệm thực
x
1
,
x
2...
Đọc tiếp
Cho phương trình m + 1 log 2 2 x + 2 log 2 x + ( m - 2 ) = 0 . Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình đã cho có hai nghiệm thực x 1 , x 2 thỏa 0 < x 1 < 1 < x 2 .
A. 2 ; + ∞
B. - 1 ; 2
C. - ∞ ; - 1
D. - ∞ ; - 1 ∪ 2 ; + ∞
Đáp án B.
Đặt t = log 2 x , khi đó m + 1 log 2 2 x + 2 log 2 x + m - 2 = 0 ⇔ m + 1 t 2 + 2 t + m - 2 = 0 (*).
Để phương trình (*) có hai nghiệm phân biệt ⇔ a = m + 1 ≠ 0 ∆ ' = 1 - m + 1 m - 2 > 0 ⇔ m ≠ - 1 m 2 - m - 3 < 0 1 .
Khi đó gọi x 1 ; x 2 lần lượt hai nghiệm của phương trình (*).
Vì 0 < x 1 < 1 < x 2 suy ra t 1 = log 2 x 1 < 0 t 2 = log 2 x 2 > 0 ⇒ t 1 t 2 = c a = m - 2 m + 1 < 0 2 .
Từ (1), (2) suy ra - 1 < m < 2 ⇔ m ∈ - 1 ; 2 là giá trị cần tìm.
Đúng 0
Bình luận (0)
Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình
9
1
-
x
+
2
(
m
-
1
)
3
1
-
x
+
1
0
có 2 nghiệm phân biệt. A. m 1 B. m -1 C. m 0 D. -1 m 0
Đọc tiếp
Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình 9 1 - x + 2 ( m - 1 ) 3 1 - x + 1 = 0 có 2 nghiệm phân biệt.
A. m > 1
B. m < -1
C. m < 0
D. -1 < m < 0
Tìm tất cả các giá trị thực của tham số m để
y
l
o
g
(
x
2
-
4
x
-
m
+
1
)
có tập xác định là R
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để y = l o g ( x 2 - 4 x - m + 1 ) có tập xác định là R
![]()
![]()
![]()
![]()
1/ Tìm các giá trị của tham số m để bpt ( m-1) x^2- ( m-1) x+1>0 nghiệm đúng vs mọi giá trị của x. 2/ Tìm giá trị của tham số m để pt x^2 - ( m-2) x+m^2 -4m=0 có 2 nghiệm trái dấu. 3/ Tìm giá trị của tham số m để pt x^2 -mx+1=0 có 2 nghiệm phân biệt.
Bài 2:
Để phương trình có hai nghiệm trái dấu thì (m-2)(m+2)<0
hay -2<m<2
Đúng 0
Bình luận (0)