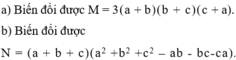Từ đẳng thức đã cho suy ra a 3   +   b 3   +   c 3 – 3abc = 0

b 3   +   c 3 = (b + c)( b 2   +   c 2 – bc)

= (b + c)[ ( b   +   c ) 2 – 3bc]

= ( b   +   c ) 3 – 3bc(b + c)

=> a 3   +   b 3   +   c 3 – 3abc = a 3   +   ( b 3   +   c 3 ) – 3abc

ó a 3   +   b 3   +   c 3 – 3abc = a 3   +   ( b   +   c ) 3 – 3bc(b + c) – 3abc

ó a 3   +   ( b 3   +   c 3 ) – 3abc = (a + b + c)( a 2   –   a ( b   +   c )   +   ( b   +   c ) 2 ) – [3bc(b + c) + 3abc]

ó a 3   +   ( b 3   +   c 3 ) – 3abc = (a + b + c)( a 2   –   a ( b   +   c )   +   ( b   +   c ) 2 ) – 3bc(a + b + c)

ó a 3   +   ( b 3   +   c 3 ) – 3abc = (a + b + c)( a 2   –   a ( b   +   c )   +   ( b   +   c ) 2 – 3bc)

ó a 3   +   ( b 3   +   c 3 ) – 3abc = (a + b + c)( a 2 – ab  - ac + b 2 + 2bc + c 2   – 3bc)

ó a 3   +   ( b 3   +   c 3 ) – 3abc = (a + b + c)( a 2   +   b 2   +   c 2 – ab – ac – bc)

Do đó nếu a 3   +   ( b 3   +   c 3 ) – 3abc = 0 thì a + b + c  = 0 hoặc a 2   +   b 2   +   c 2 – ab – ac – bc = 0

Mà a 2   +   b 2   +   c 2 – ab – ac – bc = .[ ( a   –   b ) 2   +   ( a   –   c ) 2   +   ( b   –   c ) 2 ]

Nếu ( a   –   b ) 2   +   ( a   –   c ) 2   +   ( b   –   c ) 2 = 0 ó  suy ra a = b = c

Vậy a 3   +   ( b 3   +   c 3 ) = 3abc thì a = b = c hoặc a + b + c = 0

Đáp án cần chọn là: C

Từ đẳng thức đã cho suy nghĩ a 3   +   b 3   +   c 3 – 3abc = 0

B 3   +   c 3   =   ( b   +   c ) ( b 2   +   c 2   –   b c )     =   ( b   +   c ) [ ( b   +   c ) 2   –   3 b c ] 4 =   ( b   +   c ) 3   –   3 b c ( b   +   c )

= >   a 3   +   b 3   +   c 3   –   3 a b c   =   a 3   +   ( b 3   +   c 3 )   –   3 a b c     ⇔   a 3   +   b 3   +   c 3   –   3 a b c   =   a 3   +   ( b 3   +   c 3 )   –   3 b c ( b   +   c )   –   3 a b c     ⇔   a 3   +   b 3   +   c 3   –   3 a b c   =   ( a   +   b   +   c ) ( a 2   –   a ( b   +   c )   +   ( b   +   c ) 2 )   –   [ 3 b c ( b   +   c )   +   3 a b c ]     ⇔   a 3   +   b 3   +   c 3   –   3 a b c   =   ( a   +   b   +   c ) ( a 2   –   a ( b   +   c )   +   ( b   +   c ) 2 )   –   3 b c )     ⇔   a 3   +   b 3   +   c 3   –   3 a b c   =   ( a   +   b   +   c ) ( a 2   –   a b   –   a c   +   b 2   +   2 b c   +   c 2   –   3 b c )     ⇔   a 3   +   b 3   +   c 3   –   3 a b c   =   ( a   +   b   +   c ) ( a 2   +   b 2   +   c 2   –   a b   –   a c   –   b c )

Do đó nếu a 3   +   b 3   +   c 3 – 3abc = 0 thì a + b + c = 0 hoặc a 2   +   b 2   +   c 2   – ab – ac – bc = 0

Mà a 2   +   b 2   +   c 2   – ab – ac – bc = .[ ( a   –   b ) 2   +   ( a   –   c ) 2   +   ( b   –   c ) 2 ]

Suy ra a = b = c

Đáp án cần chọn là: B

Bài 1: 

$a^3+b^3+c^3=3abc$

$\Leftrightarrow (a+b)^3-3ab(a+b)+c^3-3abc=0$

$\Leftrightarrow [(a+b)^3+c^3]-[3ab(a+b)+3abc]=0$

$\Leftrightarrow (a+b+c)[(a+b)^2-c(a+b)+c^2]-3ab(a+b+c)=0$
$\Leftrightarrow (a+b+c)[(a+b)^2-c(a+b)+c^2-3ab]=0$

$\Leftrightarrow (a+b+c)(a^2+b^2+c^2-ab-bc-ac)=0$

$\Rightarrow a+b+c=0$ hoặc $a^2+b^2+c^2-ab-bc-ac=0$

Xét TH $a^2+b^2+c^2-ab-bc-ac=0$

$\Leftrightarrow 2(a^2+b^2+c^2)-2(ab+bc+ac)=0$

$\Leftrightarrow (a-b)^2+(b-c)^2+(c-a)^2=0$
$\Rightarrow a-b=b-c=c-a=0$

$\Leftrightarrow a=b=c$

Vậy $a^3+b^3+c^3=3abc$ khi $a+b+c=0$ hoặc $a=b=c$

Áp dụng vào bài:

Nếu $a+b+c=0$

$A=\frac{-c}{c}+\frac{-b}{b}+\frac{-a}{a}=-1+(-1)+(-1)=-3$

Nếu $a=b=c$

$P=\frac{a+a}{a}+\frac{b+b}{b}+\frac{c+c}{c}=2+2+2=6$

a: Ta có: \(a+b+c=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}a+b=-c\\a+c=-b\\b+c=-a\end{matrix}\right.\)

Ta có: a+b+c=0

\(\Leftrightarrow\left(a+b+c\right)^3=0\)

\(\Leftrightarrow a^3+b^3+c^3+3\left(a+b\right)\left(a+c\right)\left(b+c\right)=0\)

\(\Leftrightarrow a^3+b^3+c^3-3abc=0\)

\(\Leftrightarrow a^3+b^3+c^3=3abc\)

b: Ta có: \(a^3+b^3+c^3=3abc\)

\(\Leftrightarrow a^3+b^3+c^3-3abc=0\)

\(\Leftrightarrow\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc=0\)

\(\Leftrightarrow\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2\right)-3ab\left(a+b+c\right)=0\)

\(\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)=0\)

\(\Leftrightarrow a+b+c=0\)

a) \(a^3+b^3+c^3=3abc\Leftrightarrow\left(a+b\right)^3+c^3-3a^2b-3ab^2-3abc=0\Leftrightarrow\left(a+b+c\right)\left[\left(a+b\right)^2-\left(a+b\right)c+c^2\right]-3ab\left(a+b+c\right)=0\Leftrightarrow\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)=0\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)=0\)(đúng do a+b+c = 0)

b) Ta có: \(\left\{{}\begin{matrix}\left(a-b\right)^2\ge0\\\left(b-c\right)^2\ge0\\\left(c-a\right)^2\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a^2+b^2\ge2ab\\b^2+c^2\ge2bc\\c^2+a^2\ge2ac\end{matrix}\right.\Rightarrow a^2+b^2+c^2\ge ab+ac+bc\)

\(ĐTXR\Leftrightarrow a=b=c\), mà a,b,c đôi một khác nhau => Đẳng thức không xảy ra\(\Rightarrow a^2+b^2+c^2>ab+ac+bc\Rightarrow a^2+b^2+c^2-ab-ac-bc>0\)

Ta có: ​\(a^3+b^3+c^3=3abc\Leftrightarrow\left(a+b\right)^3+c^3-3a^2b-3ab^2-3abc=0\Leftrightarrow\left(a+b+c\right)\left[\left(a+b\right)^2-\left(a+b\right)c+c^2\right]-3ab\left(a+b+c\right)=0\Leftrightarrow\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)=0\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)=0\)​\(\Rightarrow a+b+c=0\)( do (1))

a: Ta có: a+b+c=0

\(\Leftrightarrow\left\{{}\begin{matrix}a+b=-c\\a+c=-b\\b+c=-a\end{matrix}\right.\)

Ta có: a+b+c=0

\(\Leftrightarrow\left(a+b+c\right)^3=0\)

\(\Leftrightarrow a^3+b^3+c^3+3\left(a+b\right)\left(b+c\right)\left(a+c\right)=0\)

\(\Leftrightarrow a^3+b^3+c^3-3abc=0\)

\(\Leftrightarrow a^3+b^3+c^3=3abc\)

b: Ta có: \(a^3+b^3+c^3=3abc\)

\(\Leftrightarrow\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc=0\)

\(\Leftrightarrow\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2\right)-3ab\left(a+b+c\right)=0\)

\(\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)=0\)

\(\Leftrightarrow a+b+c=0\)

a+b+c=abc?? =))

\(a^3+b^3+c^3=3abc\\ \Rightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)+3abc=3abc\\ \Rightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)=0\\ \Rightarrow\left[{}\begin{matrix}a+b+c=0\\a^2+b^2+c^2-ab-bc-ca=0\left(vô.lí\right)\end{matrix}\right.\)

Vậy a+b+c=0

+) Ta có: a 3 + b 3 = a + b 3 - 3 a b a + b

Thật vậy, VP = a + b 3  – 3ab (a + b)

= a 3 + 3 a 2 b + 3 a b 2 + b 3 - 3 a 2 b - 3 a b 2

= a 3 + b 3  = VT

Nên  a 3 + b 3 + c 3 = a + b 3 - 3 a b a + b + c 3  (1)

Ta có: a + b + c = 0 ⇒ a + b = - c (2)

Thay (2) vào (1) ta có:

a 3 + b 3 + c 3 = - c 3 - 3 a b - c + c 3 = - c 3 + 3 a b c + c 3 = 3 a b c

Vế trái bằng vế phải nên đẳng thức được chứng minh.

Ta có: a + b + c = 0

⇒ a + b = -c ⇒ (a + b)3 = (-c)3

⇒ a3 + b3 + 3ab(a + b) = -c3 ⇒ a3 + b3 + 3ab(-c) + c3 = 0

⇒ a3 + b3 + c3 = 3abc