Gọi k là cặp số thực(x,y) #0 thỏa mãn :
\(\left(x^2+1\right)\left(x^2+y^2\right)-4x^2y=0\), vậy k=...
Gọi k là các cặp số thực ( x0 ; y0) khác 0 thỏa mãn : ( x2 + 1)(x2+y2) - 4x2y = 0 . Vậy k= ?
mk đưa lun kết quả : k = 2..check mk nhá
pt<=> x^4+y^2+x^2*y^2+x^2-4x^2y=0
=>(x^4-2x^2y+y^2)+x^2(1-2y+y^2)=0
Tìm k là số các cặp số thực (x;y) khác 0 thõa mãn:
\(\left(x^2+1\right)\left(x^2+y^2\right)-4x^2y=0\)
Tìm k là các cặp số thực (x;y) khác 0 thõa mãn: \(\left(x^2+1\right)\left(x^2+y^2\right)-4x^2y=0\)
MÌnh nghĩ thế này ko bt đúng ko
Ta có: \(\hept{\begin{cases}x^2+1\ge2x\\x^2+y^2\ge2xy\end{cases}}\)
\(\Rightarrow\left(x^2+1\right)\left(x^2+y^2\right)\ge4x^2y\)
\(\Rightarrow\left(x^2+1\right)\left(x^2+y^2\right)-4x^2y\ge0\)
Dấu = xảy ra khi x=y=1
Vậy (x;y)=(1;1)
Ta có pt \(\Leftrightarrow\left(x^2+1\right)\left(x^2+y^2\right)=4x^2y\)
Áp dụng BĐt cô-si , ta có
\(x^2+1\ge2\sqrt{x^2}=2x;x^2+y^2\ge2xy\)
Nhân vào, ta có \(\left(x^2+1\right)\left(y^2+x^2\right)\ge4x^2y\)
Dấu = xảy ra <=> x=y=1
^_^
Với mỗi số nguyên dương n, gọi Sn là số cặp cặp số nguyên (x,y) thoả mãn x^2+y^2≤n^2
Xét điểm M(a;b) bất kì nằm trog ( tính cả biên ) của hình tròn ( \(C_n\)) : \(x^2+y^2\le n^2\)
Mỗi điểm M như vậy tương ứng với 1 và chỉ 1 hình vuông đơn vị S(M) mà M là đỉnh ở goc trái , phía dưới
Từ đó suy ra \(S_n\)= số hình vuông S (M) = tổng diện tích của S(M) với \(M\in\left(C_n\right)\)
Rõ ràng các hình vuông S(M) , với \(M\in\left(C_{ }_n\right)\)đều nằm trog hình tròn \(\left(C_{n+\sqrt{2}}\right):x^2+y^2\le\left(n+\sqrt{2}\right)^2\)
Do đó : \(S_n\le\pi\left(n+\sqrt{2}\right)^2\)(1)
Tương tự như vậy , ta thấy các hình vuông S(M) , với \(M\in\left(C_n\right)\)phủ kín hình tròn
\(\left(C_{n-\sqrt{2}}\right):x^2+y^2\le\left(n-\sqrt{2}\right)^2\)vì thế \(S_n\ge\pi\left(n-\sqrt{2}\right)^2\)(2)
Từ (1) và (2) suy ra \(\sqrt{\pi}\left(n-\sqrt{2}\right)\le\sqrt{S_n}\le\sqrt{\pi}\left(n+\sqrt{2}\right)\)
suy ra \(\sqrt{\pi}\left(1-\frac{\sqrt{2}}{n}\right)\le\frac{\sqrt{S_n}}{n}\le\sqrt{\pi}\left(1+\frac{\sqrt{2}}{n}\right)\)
Mà lim \(\sqrt{\pi}\left(1-\frac{\sqrt{2}}{n}\right)\)= lim\(\sqrt{\pi}\left(1+\frac{\sqrt{2}}{n}\right)=\sqrt{\pi}\)nên lim \(\sqrt{\frac{S_n}{n}}=\sqrt{\pi}\)
@ Huy @ Bài làm đánh đẹp lắm. Nhưng cô cũng không hiểu được rõ ràng là toán 6 sao có lim, phương trình đường tròn;... ( lớp 11 , 12 ) ở đây.
Lần sau chú ý giải Toán 6 không cần dùng kiến thức quá cao nhé.
Tuy nhiên đề bài bạn thiếu. Lần sau em có thể sửa lại đề bài trước rồi hẵng làm nha.
1, với giá trị nào của k thì pt x-ky=-1 nhận cặp số (1;2) làm nghiệm?
a, k=2 b, k=1 c, k=-1 d, k=0
2, cặp số (x0; y0) là nghiệm của hệ pt \(\left\{{}\begin{matrix}x-y=-2\\x=1\end{matrix}\right.\) giá trị biểu thức \(x^2_0+y_0\) bằng
a, 4 b,5 c, 10 d, 7
3, hàm số y=5x2 nghịch biến khi
a, x>0 b, x<0 c, x\(\in\)R d, x≠0
4, tam giác ABC có 3 góc nhọn nội tiếp đường tròn tâm O biết sđ \(\stackrel\frown{AC}\)\(=80^o\) góc \(\widehat{ABC}\) có số đo là
a, 40o b, 80o c, 160o d, 140o
5, cho hàm số y= -2020x2 khẳng định nào sao đây ko đúng
a, hàm số nghịch biến khi x>0
b,đồ thị hàm số nằm ở phía dưới trục hoành
c, điểm O là điểm cao nhất của đồ thị
d, đồ thị hàm hố là một đường thẳng
6, cho hàm số y=f (x)=x2 giá trị của f(5) bằng
a, 10 b, -25 c, 25 d, -10
7, điểm M (-1;1) thuộc đồ thị hàm số y=(a-1)x2 khi a bằng
a, 2 b, 1 c, 0 d, -1
8, cho đường tròn tâm O bán kính 6m diện tích của đg tròn là
a, 36\(\pi\) (m2) b, 12\(\pi\) (m) c, 12\(\pi\) (m2) d, 36\(\pi\) (m)
9, phương trình nào sau đây có 2 nghiệm phân biệt
a, x2-x+1=0 b, x2-2x+1=0 c, x2-x-1=0 d, 25x2=0
10, pt 5x2-x-10=0 có toonge 2 nghiệm bằng
a, -1 b, 1 c, \(\dfrac{-1}{5}\) d, \(\dfrac{1}{5}\)
Câu 10: B
Câu 9: C
Câu 8: A
Câu 7: A
Câu 6: C
Câu 5:D
Câu 4: A
Câu 3: B
Câu 2: A
Câu 1; B
Cho x là số nguyên dương và y là số thực. Có tất cả bao nhiêu cặp số \(\left(x;y\right)\) thỏa mãn \(ln\left(1+x+2y\right)=2y+3x-10\) ?
tìm tất cả các cặp số thực (x;y) sao cho y là số nhỏ nhất thoả mãn điều kiện \(x^2+5y^2+2y+4xy-3=0\)
\(x^2+5y^2+2y+4xy-3=0\)
\(\Leftrightarrow\)\((x^2+4xy+4y^2)+(y^2+2y+1)=4\)
\(\Leftrightarrow\)\((x+2y)^2+(y+1)^2=4\)
\(\Leftrightarrow\)\((x+2y)^2=4-(y+1)^2\)
\(\Leftrightarrow\)\((x+2y)^2=(2-y-1)(2+y+1)\)
\(\Leftrightarrow\)\((x+2y)^2=(1-y)(3+y)\)
\(Vì \) \((x+2y)^2\geq0\)
\(\Rightarrow\)\((1-y)(3+y)\geq0\)
\(\Rightarrow\)\(\left[\begin{array}{}
\begin{cases}
1-y\geq0\\
3+y\geq0
\end{cases}\\
\begin{cases}
1-y\leq0\\
3+y\leq0
\end{cases}
\end{array} \right.\)
\(\Rightarrow\)\(\left[\begin{array}{}
\begin{cases}
y\leq1\\
y\geq-3
\end{cases}\\
\begin{cases}
y\geq1\text{(Vô lí)}\\
y\leq-3\text{(Vô lí)}
\end{cases}
\end{array} \right.\)\(\Rightarrow\)\(-3\leq y\leq1\)
\(\text{Mà y là số nhỏ nhất}\)
\(\Rightarrow\)\(y=-3\)
\(\Rightarrow\)\(x+2.(-3)=0\text{ (Vì }(x+2y)^2\geq0)\)
\(\Rightarrow\)\(x=6\)
\(\text{Vậy cặp số (x,y) thỏa mãn yêu cầu bài toán là: (6;-3)}\)
Nếu mình đúng cho mình xin 1 like nha
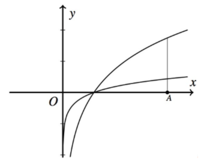
Cho hai số thực dương a, b khác 1 và đồ thị của các hàm số y = log a x , y = log b x như hình vẽ bên. Gọi d là đường thẳng song song với trục Oy và cắt trục hoành tại điểm A có hoành độ x=k(k>1) Gọi S1 là diện tích hình phẳng giới hạn bởi y = log a x , d và trục hoành; S2 là diện tích hình phẳng giới hạn bởi y = log b x , d và trục hoành. Biết S1 = 4S2. Mệnh đề nào sau đây đúng ?
A. b = a 4
B. a = b 4
C. b = a 4 ln 2
D. a = b 4 ln 2
Theo giả thiết và công thức tích phân từng phần, ta có:
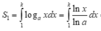
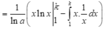
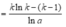
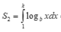
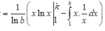
![]()
Vậy ![]()
![]()
Chọn đáp án A.
Có bao nhiêu cặp số thực (x; y) sao cho (x+1)y, xy và (x-1)y là số đo ba góc một tam giác (tính theo rad) và sin 2 [ ( x + 1 ) y ] = sin 2 ( x y ) + sin 2 [ ( x - 1 ) y ]
A. 4.
B. 1
C. 3.
D. 2.
Đáp án B
Theo giả thiết có 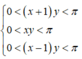 và
và
![]()

Và thay vào đẳng thức điều kiện có:
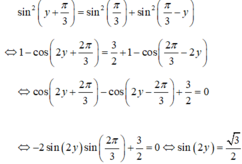
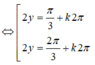
Đối chiếu với điều kiện nhận 