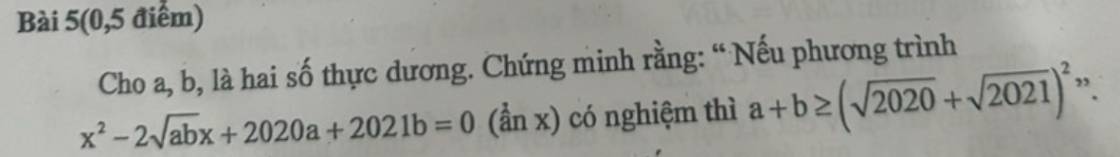\(\text{Điều kiện: }x\geq-1\)
                 \(x^2-2x-2\geq0(*)\)

\(x+2=\sqrt{x^2-2x-2}+2\sqrt{x+1}\)
\(\Leftrightarrow\)\(x+2-\sqrt{x^2-2x-2}-2\sqrt{x+1}=0\)
\(\Leftrightarrow\)\(\dfrac{(x+2)^2-x^2+2x+2}{x+2+\sqrt{x^2-2x-2}}-2\sqrt{x+1}=0\)
\(\Leftrightarrow\)\(\dfrac{x^2+4x+4-x^2+2x+2}{x+2+\sqrt{x^2-2x-2}}-2\sqrt{x+1}=0\)
\(\Leftrightarrow\)\(\dfrac{6x+6}{x+2+\sqrt{x^2-2x-2}}-2\sqrt{x+1}=0\)
\(\Leftrightarrow\)\(\sqrt{x+1}(\dfrac{6\sqrt{x+1}}{x+2}-2)=0\)
\(\Leftrightarrow\)\(\left[\begin{array}{} \sqrt{x+1}=0\\ 6\sqrt{x+1}=2(x+2) \end{array} \right.\)
\(TH1:\sqrt{x+1}=0 \)
\(\Leftrightarrow\)\(x+1=0\)
\(\Leftrightarrow\)\(x=-1(\text{thỏa mãn (*))}\)
\(TH2:6\sqrt{x+1}=2(x+2)\text{ Điều kiện: }x\geq=-2\)
\(\Leftrightarrow\)\(36x+36=4x^2+16x+16\)
\(\Leftrightarrow\)\(4x^2-20x-20=0\)
\(\Leftrightarrow\)\(x^2-5x-5=0\)
\(\text{Ta có }\bigtriangleup = 25+4*5=45>0 \)
\(\text{Phương trình có 2 nghiệm phân biệt:} \)
\(\begin{cases} x_1=\dfrac{5+3\sqrt{5}}{2}(T/m)\\ x_2=\dfrac{5-3\sqrt{5}}{2}(KTM) \end{cases}\)
\(\text{Vậy tập nghiệm của phương trình là: }S=\text{{-1;\dfrac{5+3\sqrt5}{2}}}\)

Cho đường tròn tâm O có đường kính AB bằng 2R (R>0). Gọi C là điểm chính giữa cung AB và M là điểm thuộc cung BC (M khác B và C). Tiếp tuyến tại M của nửa đuognừ tròn tâm O cắt các đường thẳng OC và AB theo thứ tự tại S và K. AM cắt OC tại I.
1. Tính diện tích hình viên phân được giới hạn bởi AC và cung AC (Tính theo R).
2. Chứng minh tứ giác OIMB là tứ giác nội tiếp và SI=SM.
3. Chứng minh AC là tiếp tuyến của đường tròn ngoại tiếp tam giác ICM.
4. Gọi H là hình chiếu của M trên AB. Chứng minh BH.AK=BK.AH.

a,Xét tứ giác ABCD có:
\(\widehat{CBD}=\widehat{CAD}(=90^o)\)
\(\Rightarrow \)ABCD nội tiếp
b,Xét \(\bigtriangleup EBD\) và \(\bigtriangleup EAC\) có:
\(\widehat{CED}\): chung

\(\widehat{EBD}=\widehat{EAC}(=90^o)\)
\(\Rightarrow \)\(\bigtriangleup EBD = \bigtriangleup EAC(g-g)\)
\(\Rightarrow \)\(\frac{EB}{ED}=\frac{EA}{EC}\)
\(\Rightarrow \)\(EB.EC=EA.ED\)
c,\(\Rightarrow \)\(\frac{EB}{EA}=\frac{ED}{EC}\)
Xét \(\bigtriangleup EBA\) và \(\bigtriangleup EDC\) có:
\(\frac{EB}{EA}=\frac{ED}{EC}\)
\(\widehat{CED}\): chung
\(\Rightarrow \)\(\bigtriangleup EBA = \bigtriangleup EDC(c-g-c)\)
Ta có:\(\widehat{FED}=\widehat{FCD}(=\frac{1}{2}sđ\stackrel\frown{ED})\)
   Mà \(\widehat{EAB} =\widehat{ECD}(\bigtriangleup EBD = \bigtriangleup EAC)\)
\(\Rightarrow \)\(\widehat{FED}+\widehat{EAB}=\widehat{FCD}+\widehat{ECD}=\widehat{ECF}\)
Vì \(\widehat{ECF}\) là góc nội tiếp chắn nửa đường tròn \(\Rightarrow \) \(\widehat{ECF}=90^o\)
\(\Rightarrow \)\(\widehat{FED}+\widehat{EAB}=90^o\)
\(\Rightarrow \)\(EF\perp AB\)
d,Ta có: \(\widehat{FDE}\) là góc nội tiếp chắn nửa đường tròn\(\Rightarrow \widehat{FDE}=90^o\)
\(\Rightarrow FD \perp ED\)
Mà \(CA\) là đường cao \(\Rightarrow\) \(CA \perp ED\)
\(\Rightarrow FD // CA\) Hay \(FD // CH\)
Lại có: \(\widehat{ECF}=90^o\)
\(\Rightarrow\)\(EC \perp CF\)

Mà 

Giả sử \(x^3+x^2+2025\) là số chính phương nhỏ hơn 10000. Ta có phương trình:
\(x^3+x^2+2025 =k^2(k \in N,k^2<10000 \Leftrightarrow k<100)\)
\(\Leftrightarrow \)\(2025=k^2-x^2(x+1)\)
\(\Leftrightarrow \)\(2025=(k-x\sqrt{x+1})(k+x\sqrt{x+1})\)
Mà \(k-x\sqrt{x+1} < k+x\sqrt{x+1}< 100\)(Vì \(k < 100\))
\(\Rightarrow \)\(\left[\begin{array}{} \begin{cases} k+x\sqrt{x+1}=81\\ k-x\sqrt{x+1}=25 \end{cases}\\ \begin{cases} k+x\sqrt{x+1}=75\\ k-x\sqrt{x+1}=27 \end{cases}\\ \end{array} \right.\)
\(\Leftrightarrow\)\(\left[\begin{array}{} \begin{cases} 2k=106\\ k-x\sqrt{x+1}=25 \end{cases}\\ \begin{cases} 2k=102\\ k-x\sqrt{x+1}=27 \end{cases}\\ \end{array} \right.\)
\(\Leftrightarrow\)\(\left[\begin{array}{} \begin{cases} k=53\\ 53-x\sqrt{x+1}=25 \end{cases}\\ \begin{cases} k=51\\ 51-x\sqrt{x+1}=27 \end{cases}\\ \end{array} \right.\)
\(\Leftrightarrow\)\(\left[\begin{array}{} \begin{cases} k=53\\ x\sqrt{x+1}=28 \end{cases}\\ \begin{cases} k=51\\ x\sqrt{x+1}=24 \end{cases}\\ \end{array} \right.\)

\(\Leftrightarrow\)\(\left[\begin{array}{} \begin{cases} k=53\\ x^3+x^2-784=0 \end{cases}\\ \begin{cases} k=51\\ x^3+x^2-576=0 \end{cases}\\ \end{array} \right.\)
\(\Leftrightarrow\)\(\left[\begin{array}{} \begin{cases} k=53\\ x^3+x^2-784=0(PTVN) \end{cases}\\ \begin{cases} k=51\\ x^3-8x^2+9x^2-72x+72x-576=0 \end{cases}\\ \end{array} \right.\)
\(\Leftrightarrow\)\(\begin{cases} k=51\\ (x-8)(x^2+9x+72)=0 \end{cases}\)
\(\Leftrightarrow\)\(\begin{cases} k=51(t/m)\\ \left[\begin{array}{} x=8(t/m)\\ (x+\frac{9}{2})^2+\frac{207}{4}=0(PTVN) \end{array} \right. \end{cases}\)
Vậy chỉ có giá trị \(x=8\) thỏa mãn yêu cầu bài toán.
P/s: Cái c/m vô nghiệm kia mình không biết làm. Chỉ biết bấm máy tính không ra nghiệm nguyên

làm hết hả bạn ?

Ta có : \(x^2-2x-1=0 \)
\(\Leftrightarrow \)\((x-1)^2=2\)
\(\Leftrightarrow \)\(\left[\begin{array}{} x-1=\sqrt{2}\\ x-1=-\sqrt{2} \end{array} \right.\)
Đặt P = \(\dfrac{x^6-6x^5+12x^4-8x^3+2015}{x^6-8x^3-12x^2+6x+2015}\)
          =\(\dfrac{(x^6-2x^5-x^4)-(4x^5-8x^4-4x^3)+(5x^4-10x^3-5x^2)-(2x^3-4x^2-2x)+(x^2-2x-1)+2016} {(x^6-2x^5-x^4)+(2x^5-4x^4-2x^3)+(5x^4-10x^3-5x^2)+(4x^3-8x^2-4x)+(x^2-2x-1)+12x+2016}\)
         =\(\dfrac{x^4(x^2-2x-1)-4x^3(x^2-2x-1)+5x^2(x^2-2x-1)-2x(x^2-2x-1)+(x^2-2x-1)+2016} {x^4(x^2-2x-1)+2x^3(x^2-2x-1)+5x^2(x^2-2x-1)+4x(x^2-2x-1)+(x^2-2x-1)+12x+2016}\)
         =\(\dfrac{2016}{12x + 2016}\)
         =\(\dfrac{2016}{12(x+1)+2004}\)
         =\(\dfrac{168}{x+1+167}\)
         =\(\left[\begin{array}{} \dfrac{168}{\sqrt{2}+167}\\ \dfrac{168}{-\sqrt{2}+167} \end{array} \right.\)
Chú thích: Hình như mẫu là \(-6x\) chứ không phải \(6x \) bạn ạ. Hay là mình phân tích sai thì cho mình xin lỗi nhé.

Vì \(\dfrac{70}{61}\)>x>\(\dfrac{61}{61}\)
\(\Rightarrow \)x \(\in\) {\(\dfrac{62}{61}\);\(\dfrac{63}{61}\);\(\dfrac{64}{61}\);\(\dfrac{65}{61}\)}
Ngoài ra bạn có thể chọn các số khác nữa nhé