Bài 1:
a: Thay x=-1 và y=-1 vào (d1), ta được:
\(-\left(m+1\right)+2=-1\)
=>-m-1+2=-1
=>-m+1=-1
=>-m=-2
=>m=2
b: Tọa độ điểm B là:
\(\left\{{}\begin{matrix}-2x+1=x+2\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-3x=1\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{3}\\y=-\dfrac{1}{3}+2=\dfrac{5}{3}\end{matrix}\right.\)
vậy: \(B\left(-\dfrac{1}{3};\dfrac{5}{3}\right)\)
c: Thay x=-1/3 và y=5/3 vào (d1), ta được:
\(-\dfrac{1}{3}\left(m+1\right)+2=\dfrac{5}{3}\)
=>\(-\dfrac{1}{3}\left(m+1\right)=-\dfrac{1}{3}\)
=>m+1=1
=>m=0
d: Vì \(\left\{{}\begin{matrix}-2=-2\\1\ne2\end{matrix}\right.\)
nên (d2)//(d4)
Vì \(1\ne-2\)
nên (d3) cắt (d4)
Bài 2:
a: Xét ΔAEI có
K là trung điểm của AI
KM//EI
Do đó: M là trung điểm của AE
=>AM=ME
Xét hình thang BMKH có
I là trung điểm của KH
IE//MK//BH
Do đó:E là trung điểm của MB
=>ME=EB
=>AM=ME=EB
b: Xét ΔABC có MN//BC
nên \(\dfrac{MN}{BC}=\dfrac{AM}{AB}\)
=>\(\dfrac{MN}{30}=\dfrac{1}{3}\)
=>MN=30/3=10(cm)
Xét ΔABC có EF//BC
nên \(\dfrac{EF}{BC}=\dfrac{AE}{AB}\)
=>\(\dfrac{EF}{30}=\dfrac{2}{3}\)
=>\(EF=30\cdot\dfrac{2}{3}=20\left(cm\right)\)
c: Xét ΔABC có MN//BC
nên ΔAMN~ΔABC theo hệ số tỉ lệ là \(k=\dfrac{AM}{AB}=\dfrac{1}{3}\)
=>\(\dfrac{S_{AMN}}{S_{ABC}}=\left(\dfrac{1}{3}\right)^2=\dfrac{1}{9}\)
=>\(S_{AMN}=\dfrac{1}{9}\cdot S_{ABC}\)
Ta có: \(S_{AMN}+S_{BMNC}=S_{ABC}\)
=>\(S_{BMNC}=\dfrac{8}{9}\cdot S_{ABC}\)
=>\(S_{ABC}=200:\dfrac{8}{9}=225\left(cm^2\right)\)
d: Xét ΔAMN và ΔABC có
\(\widehat{AMN}=\widehat{ABC}\)(hai góc đồng vị, MN//BC)
\(\widehat{MAN}\) chung
Do đó: ΔAMN~ΔABC
=>\(k=\dfrac{AM}{AB}=\dfrac{1}{3}\)
Xét ΔAEF và ΔABC có
\(\widehat{AEF}=\widehat{ABC}\)(hai góc đồng vị, EF//BC)
\(\widehat{FAE}\) chung
Do đó: ΔAEF~ΔABC
=>\(k=\dfrac{AE}{AB}=\dfrac{2}{3}\)

















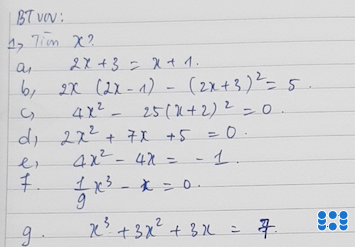

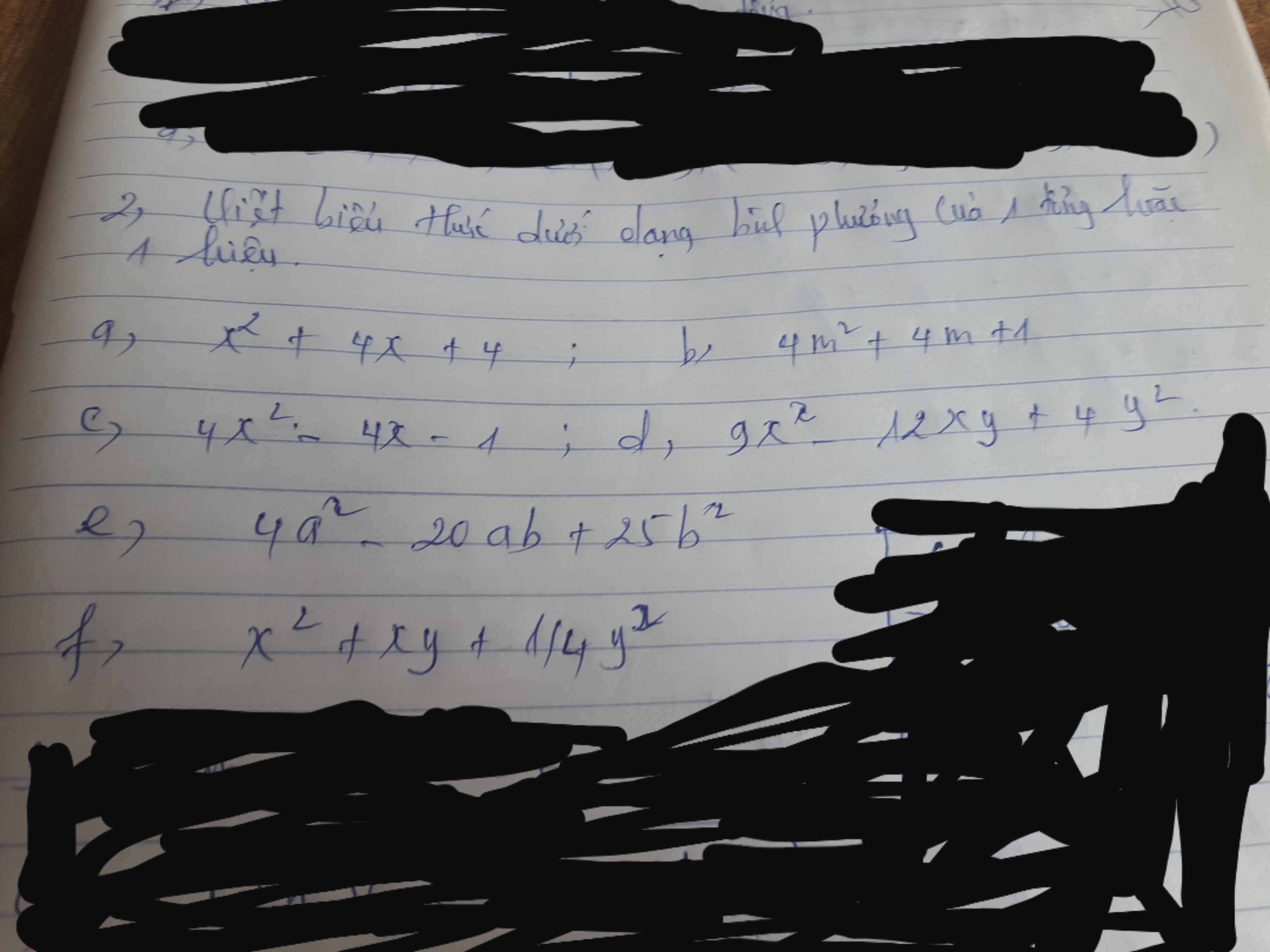



 giải thích giùm mình với
giải thích giùm mình với