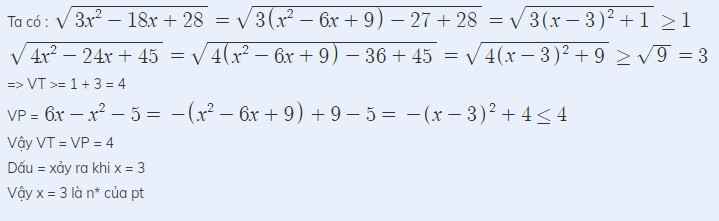a. \(x^4-10x^3+25x^2-36=0\)

=> \(x^3\left(x-3\right)-7x^2\left(x-3\right)+4x\left(x-3\right)+12\left(x-3\right)=0\)

=>\(\left(x-3\right)\left(x^3-7x^2+4x+12\right)=0\)

=>\(\left(x-3\right)\left[x^2\left(x-2\right)-5x\left(x-2\right)-6\left(x-2\right)\right]=0\)=> \(\left(x-3\right)\left(x-2\right)\left(x^2-5x-6\right)=0\)

=> \(\left(x-3\right)\left(x-2\right)\left(x+1\right)\left(x-6\right)=0\)

=>\(\left[\begin{matrix}x=3\\x=2\\x=-1\\x=6\end{matrix}\right.\)

b) \(x^4\) - \(^{9x^2}\) - 24x - 16 = 0

=> \(x^3\left(x-4\right)+4x^2\left(x-4\right)+7x\left(x-4\right)+4\left(x-4\right)=0\)=>\(\left(x-4\right)\left(x^3+4x^2+7x+4\right)=0\)

=> \(\left(x-4\right)\left[x^2\left(x+1\right)+3x\left(x+1\right)+4\left(x+1\right)\right]=0\)=>\(\left(x-4\right)\left(x+1\right)\left(x^2+3x+4\right)=0\)

=> \(\left(x-4\right)\left(x+1\right)=0\) (vì x^2 + 3x + 4> 0)

=>\(\left[\begin{matrix}x=4\\x=-1\end{matrix}\right.\)

a,pt\(\Leftrightarrow\left(x^4-10x^3+25x\right)-36=0\)\(\Leftrightarrow\left(x^2-5x\right)^2-36=0\)

\(\Leftrightarrow\left(x^2-5x-6\right)\left(x^2-5x+6\right)=0\)\(\Leftrightarrow\left[\begin{matrix}x^2-5x-6=0\\x^2-5x+6=0\end{matrix}\right.\)

\(\Leftrightarrow\left[\begin{matrix}\left(x+1\right)\left(x-6\right)=0\\\left(x-2\right)\left(x-3\right)=0\end{matrix}\right.\)\(\Leftrightarrow\left[\begin{matrix}x=-1,x=6\\x=2,x=3\end{matrix}\right.\)

vậy pt có 4 nghiệm x=(-1,6,2,3)

pt\(\Leftrightarrow x^4-\left(9x^2+24x+16\right)=0\)\(\Leftrightarrow\left(x^2\right)^2-\left(3x+4\right)^2=0\)\(\Leftrightarrow\left(x^2-3x-4\right)\left(x^2+3x+4\right)=0\)\(\Leftrightarrow\left[\begin{matrix}x^2-3x-4=0\\x^2+3X+4=0\end{matrix}\right.\)

\(\Leftrightarrow\left[\begin{matrix}\left(x-4\right)\left(x+1\right)=0\\x^2+3x+4>0\end{matrix}\right.\)\(\Leftrightarrow x=4,x=-1\)

vậy pt có nghiệm x=(4,-1)

\(\Leftrightarrow x^4-x^3+x^3-x^2-8x^2+8x+16x-16=0\\ \Leftrightarrow\left(x-1\right)\left(x^3+x^2-8x+16\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x^3+4x^2-3x^2-12x+4x+16\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+4\right)\left(x^2-3x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-4\\\left(x-\dfrac{3}{2}\right)^2+\dfrac{7}{4}=0\left(vô.n_o\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-4\end{matrix}\right.\)

\(x^4-9x^2+24x-16=\)\(0\)

\(\Leftrightarrow x^4-\left(9x^2-24x+16\right)=0\)

\(\Leftrightarrow x^4-\left(3x-4\right)^2=0\)

\(\Leftrightarrow\left(x^2+3x-4\right)\left(x^2-3x+4\right)=0\)

\(\Leftrightarrow\left(x+4\right)\left(x-1\right)\left[\left(x-\frac{3}{2}\right)^2+\frac{7}{4}\right]=0\)

Vì \(\left(x-\frac{3}{2}\right)^2+\frac{7}{4}>0\forall x\)nên:

\(\left(x+4\right)\left(x-1\right)=0:\left[\left(x-\frac{3}{2}\right)^2+\frac{7}{4}\right]\)

\(\Leftrightarrow\left(x+4\right)\left(x-1\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x+4=0\\x-1=0\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}x=-4\\x=1\end{cases}}\)

Vậy phương trình có tập nghiệm \(S=\left\{1;-4\right\}\)

\(x^4=6x^2+12x+\)\(8\)

\(\Leftrightarrow x^4-2x^2+1=4x^2+12x+9\)

\(\Leftrightarrow\left(x^2-1\right)^2=\left(2x+3\right)^2\)

\(\Leftrightarrow|x^2-1|=|2x+3|\)\(|\)

xét các trường hợp:

- Trường hợp 1:

\(x^2-1=2x+3\)

\(\Leftrightarrow x^2-1-2x-3=0\)

\(\Leftrightarrow x^2-2x-4=0\)

\(\Leftrightarrow\left(x-1\right)^2-5=0\Leftrightarrow\left(x-1\right)^2=5\)

\(\Leftrightarrow\orbr{\begin{cases}x-1=\sqrt{5}\\x-1=-\sqrt{5}\end{cases}\Leftrightarrow\orbr{\begin{cases}x=1+\sqrt{5}\\x=1-\sqrt{5}\end{cases}}}\)

-Trường hợp 2:

\(x^2-1=-2x-3\)

\(\Leftrightarrow x^2-1+2x+3=0\)

\(\Leftrightarrow x^2+2x+2=0\)

\(\Leftrightarrow\left(x+1\right)^2+1=0\)

\(\Leftrightarrow\left(x+1\right)^2=-1\left(vn\right)\)(vô nghiệm)

Vậy phương trình có tập nghiệm: \(S=\left\{1\pm\sqrt{5}\right\}\)

\(x^4=4x+1\)

\(\Leftrightarrow x^4+2x^2+1=2x^2+4x+2\)

\(\Leftrightarrow\left(x^2+1\right)^2=2\left(x+1\right)^2\)

\(\Leftrightarrow|x^2+1|=|x\sqrt{2}+\sqrt{2}|\)

Xét các trường hợp sau:

-Trường hợp 1:

\(x^2+1=x\sqrt{2}+\sqrt{2}\)

\(\Leftrightarrow x^2+1-x\sqrt{2}-\sqrt{2}=0\)

\(\Leftrightarrow\left(x^2-2x.\frac{\sqrt{2}}{2}+\frac{1}{2}\right)-\frac{2\sqrt{2}-1}{2}=0\)

\(\Leftrightarrow\left(x-\frac{1}{\sqrt{2}}\right)^2=\frac{2\sqrt{2}-1}{2}\)

Vì \(\frac{2\sqrt{2}-1}{2}>0\)nên:

\(\left|x-\frac{1}{\sqrt{2}}\right|=\left|\sqrt{\frac{2\sqrt{2}-1}{2}}\right|\)

Lại xét các trường hợp:

+Trường hợp 1.1:

\(x-\frac{1}{\sqrt{2}}=\frac{\sqrt{2\sqrt{2}-1}}{\sqrt{2}}\)\(\Leftrightarrow x=\frac{\sqrt{2\sqrt{2}-1}+1}{\sqrt{2}}\)

+Trường hợp 1.2:

\(x-\frac{1}{\sqrt{2}}=\frac{\sqrt{2\sqrt{2}-1}}{\sqrt{2}}\Leftrightarrow x=\frac{1-\sqrt{2\sqrt{2}-1}}{\sqrt{2}}\)

-Trường hợp 2:

\(x^2+1=-x\sqrt{2}-\sqrt{2}\)(2)

\(\Leftrightarrow x^2+1+x\sqrt{2}+\sqrt{2}=0\)

\(\Leftrightarrow\left(x^2+2x.\frac{\sqrt{2}}{2}+\frac{1}{2}\right)+\frac{1+2\sqrt{2}}{2}=0\)

\(\Leftrightarrow\left(x+\frac{1}{\sqrt{2}}\right)^2=\frac{-1-2\sqrt{2}}{2}\)(vô nghiệm)

Do đó phương trình (2) vô nghiệm.

Vậy phương trình có tập nghiệm : \(S=\left\{\frac{1\pm\sqrt{2\sqrt{2}-1}}{\sqrt{2}}\right\}\)

(x² + 5x + 6)(x² + 9x + 20) = 24

<=> (x + 2)(x + 3)(x + 4)(x + 5) - 24 = 0

<=> (x² + 7x + 10)(x² + 7x + 12) - 24 = 0 (1)

Đặt x² + 7x + 11 = t, ta có:

(1) <=> (t - 1)(t + 1) - 24 = 0

<=> t² - 1 - 24 = 0

<=> (t - 5)(t + 5) = 0

\(\Leftrightarrow\left[{}\begin{matrix}t-5=0\\t+5=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2+7x+11-5=0\\x^2+7x+11+5=0\end{matrix}\right.\)

<=> (x + 1)(x + 6) = 0 (vì \(x^2+7x+16\ge\dfrac{15}{4}>0\))

<=> x = - 1 hoặc x = - 6

~ ~ ~ ~ ~

x⁴ - 24x = 32

<=> x⁴ - 24x - 32 = 0

<=> (x² - 2x - 4)(x² + 2x + 8) = 0

<=> \(\left(x-1-\sqrt{5}\right)\left(x-1+\sqrt{5}\right)=0\) (vì \(x^2+2x+8\ge7>0\))

\(\Leftrightarrow\left[{}\begin{matrix}x=1+\sqrt{5}\\x=1-\sqrt{5}\end{matrix}\right.\)

\(x^4-9x^3+24x^2-27x+9=0\)

<=> \(x^4-3x^3+3x^2-6x^3+18x^2-18x+3x^2-9x+9=0\)

<=>\(x^2\left(x^2-3x+3\right)-6x\left(x^2-3x+3\right)+3\left(x^2-3x+3\right)=0\)

<=>\(\left(x^2-6x+3\right)\left(x^2-3x+3\right)=0\)

<=> \(\left[{}\begin{matrix}x^2-6x+3=0\\x^2-3x+3=0\end{matrix}\right.\)

Giải nốt :))

nhận thấy x = 0 không là nghiệm của phương trình

Chia 2 vế phương trình cho x², ta được : 

\(x^2-9x+24-\frac{27}{x}+\frac{9}{x^2}=0\)  ( 1 )

đặt \(t=x+\frac{3}{x}\)

( 1 ) \(\Leftrightarrow\left(x+\frac{3}{x}\right)^2-9\left(x+\frac{3}{x}\right)+18=0\)

\(\Leftrightarrow t^2-9t+18=0\Leftrightarrow\left(t-6\right)\left(t-3\right)=0\Leftrightarrow\orbr{\begin{cases}t=6\\t=3\end{cases}}\)

Khi đó : \(\orbr{\begin{cases}x+\frac{3}{x}=6\Leftrightarrow x=3\pm\sqrt{6}\\x+\frac{3}{x}=3\Leftrightarrow x\in\varnothing\end{cases}}\)

a) <=> 4x^3 - 12x^2 - x^2 + 3x + 6x - 18 = 0

<=> 4x^2 (x - 3) - x(x - 3) + 6(x - 3) = 0

<=> (x - 3)(4x^2 - x + 6) = 0

xét 2 th

. x - 3 = 0 <=> x = 3

. 4x^2 - x + 6 = 0

<=> 4x^2 + 2.(1/2)x + 1/4 + 23/4 = 0

<=> (4x + 1/2)^2 = -23/4

.... phần sau bạn tự làm nhé 

vậy pt trên có nghiệm là ...

. mik bận nên chỉ làm như vậy thôi.. những ý sau thì tách tương tự

c) => x³ + 2x² - 6x²  - 12x + 4x + 8 = 0

=> (x³ + 2x²)  -  (6x²  + 12x)  + (4x + 8) = 0

=> x². (x +2) - 6x. (x + 2) + 4.(x + 2) =0

=> (x +2).(x²  - 6x + 4) = 0

=> x+ 2 = 0 hoặc x²  - 6x + 4 = 0

+) x+ 2 =0 => x = -2

+) x²  - 6x + 4 = 0 => x²  - 2.x.3  + 9  - 5 = 0 => (x -3)²  = 5

=> x - 3 = \(\sqrt{5}\) hoặc x - 3 = - \(\sqrt{5}\)

=> x = 3 + \(\sqrt{5}\) hoặc x = 3 - \(\sqrt{5}\)

vậy...

a,ĐK: x≥4

Ta có: \(2\sqrt{x-4}-\dfrac{1}{3}\sqrt{9x-36}=4-\sqrt{x-4}\)

      \(\Leftrightarrow2\sqrt{x-4}-\sqrt{x-4}=4-\sqrt{x-4}\)

      \(\Leftrightarrow2\sqrt{x-4}=4\)

      \(\Leftrightarrow\sqrt{x-4}=2\Leftrightarrow x-4=4\Leftrightarrow x=8\left(tm\right)\)

b, ĐK: x≥2

Ta có: \(3\sqrt{x-2}-\sqrt{x^2-4}=0\)

      \(\Leftrightarrow3\sqrt{x-2}-\sqrt{\left(x-2\right)\left(x+2\right)}=0\)

      \(\Leftrightarrow\sqrt{x-2}\left(3-\sqrt{x+2}\right)=0\)

      \(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-2}=0\\3-\sqrt{x+2}=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x-2=0\\\sqrt{x+2}=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x+2=9\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=7\end{matrix}\right.\)

Ta có: \(\sqrt{9x+9}+\sqrt{4x+4}-2\sqrt{16x+16}=\sqrt{x+1}-8\)

\(\Leftrightarrow3\sqrt{x+1}+2\sqrt{x+1}-8\sqrt{x+1}-\sqrt{x+1}=-8\)

\(\Leftrightarrow\sqrt{x+1}=2\)

\(\Leftrightarrow x+1=4\)

hay x=3