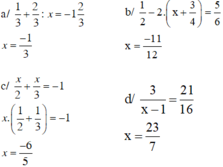123 - 23 x 1 x3 x2

Những câu hỏi liên quan
Tìm x
a/
1
3
+
2
3
:
x
−
1
2
3
b/
1
2
−
2
.
x
+
3
4
5
6
c/
x
2
+
x
3
−
1
d/ ...
Đọc tiếp
Tìm x
a/ 1 3 + 2 3 : x = − 1 2 3
b/ 1 2 − 2 . x + 3 4 = 5 6
c/ x 2 + x 3 = − 1
d/ 3 x − 1 = 21 16
Tim X
3) -12 + (2x – 9) + x= 0
4) 11 + (15 - x) = 1
5) 4 - (27 - 3) = x - (13 - 4)
6) 8 - (x - 10) = 23 - (- 4 +12)
7) 105 – 5(10 – 5x) = -20
8) (x -1)(8-2x)(3x+123) = 0
9) (x2 - 25)(x+ 10) = 0
10) x(x2+5) =
3) \(-12+2x-9+x=0\\ -21+3x=0\\ 3x=21\\ x=7\)
Đúng 1
Bình luận (2)
4)
\(11+\left(15-x\right)=1\)
\(15-x=1-11\)
\(15-x=-10\)
\(x=15-\left(-10\right)\)
\(x=25\)
5)
\(4-\left(27-3\right)=x-\left(13-4\right)\)
\(4-24=x-9\)
\(x-9=-20\)
\(x=-20+9\)
\(x=-11\)
Đúng 0
Bình luận (0)
\(3.-12+\left(2x-9\right)+x=0.\)
\(\Leftrightarrow-12+2x-9+x=0.\Leftrightarrow3x=21.\Leftrightarrow x=7.\)
Vậy \(x=7.\)
\(4.11+\left(15-x\right)=1.\Leftrightarrow11+15-x=1.\Leftrightarrow26-x=1.\Leftrightarrow x=25.\)
Vậy \(x=25.\)
\(5.4-\left(27-3\right)=x-\left(13-4\right).\Leftrightarrow4-24=x-9.\Leftrightarrow-20=x-9.\Leftrightarrow x=-11.\)
Vậy \(x=-11.\)
\(6.8-\left(x-10\right)=23-\left(-4+12\right).\Leftrightarrow8-x+10=23-8.\Leftrightarrow18-x=15.\Leftrightarrow x=3.\)
Vậy \(x=3.\)
\(7.105-5\left(10-5x\right)=-20.\Leftrightarrow105-50+25x=-20.\Leftrightarrow25x=-75.\Leftrightarrow x=-3.\)
Vậy \(x=-3.\)
\(8.\left(x-1\right)\left(8-2x\right)\left(3x+123\right)=0.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0.\\8-2x=0.\\3x+123=0.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1.\\x=4.\\x=-41.\end{matrix}\right.\)
Vậy \(x\in\left\{1;4;-41\right\}.\)
\(9.\left(x^2-25\right)\left(x+10\right)=0.\)
\(\Leftrightarrow\left(x-5\right)\left(x+5\right)\left(x+10\right)=0.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-5=0.\\x+5=0.\\x+10=0.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5.\\x=-5.\\x=-10.\end{matrix}\right.\)
Vậy \(x\in\left\{5;-5;-10\right\}.\)
\(10.x\left(x^2+5\right)=0.\Leftrightarrow x=0.\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
1. (x2 - 9x + 20)(x2 - 13x + 12) = 1680
2. (x2 + x - 2)(x2 + x - 3) = 12
3. (x2 - 9)2 = 12x + 1
4. x3 + 3x2 + 4x + 2 = 0
5. x3 + 2x2 - x - 2 = 0
cac ban giup minh voi a ![]()
2: \(\Leftrightarrow\left(x^2+x\right)^2-5\left(x^2+x\right)-6=0\)
\(\Leftrightarrow x^2+x-6=0\)
=>(x+3)(x-2)=0
=>x=-3 hoặc x=2
5: \(\Leftrightarrow\left(x+2\right)\left(x-1\right)\left(x+1\right)=0\)
hay \(x\in\left\{-2;1;-1\right\}\)
Đúng 1
Bình luận (0)
Phân tích đa thức thành nhân tử:
1) x2 - y2 - 2x + 1
2) x3 - 2x2 - x + 2
3) x2 - 2x2 - x + 2
1: =(x-1-y)(x-1+y)
3: =(x-1)(x+1)(x-2)
Đúng 1
Bình luận (0)
Rút gọn biểu thức x3(x+2) – x(x3 + 23) – 2x(x2 – 22)
Ta có:
x3(x+2) – x(x3 + 23) – 2x(x2 – 22)
= x3 . x + x3 . 2 – (x . x3 + x . 23) – ( 2x . x2 – 2x . 22)
= x4 + 2x3 – (x4 + 8x ) – (2x3 – 8x)
= x4 + 2x3 – x4 – 8x – 2x3 + 8x
= (x4 – x4) + (2x3 – 2x3) + (-8x + 8x)
= 0
Đúng 0
Bình luận (0)
Giải các phương trình:
a
x
-
3
2
+
x
+
4
2
23
−
3
x...
Đọc tiếp
Giải các phương trình:
a x - 3 2 + x + 4 2 = 23 − 3 x b ) x 3 + 2 x 2 − x - 3 2 = ( x − 1 ) x 2 − 2 c ) x - 1 3 + 0 , 5 x 2 = x x 2 + 1 , 5 d ) x ( x − 7 ) 3 − 1 = x 2 − x − 4 3 e ) 14 x 2 − 9 = 1 − 1 3 − x f ) $ 2 x x + 1 = x 2 − x + 8 ( x + 1 ) ( x − 4 )
a)
( x − 3 ) 2 + ( x + 4 ) 2 = 23 − 3 x ⇔ x 2 − 6 x + 9 + x 2 + 8 x + 16 = 23 − 3 x ⇔ x 2 − 6 x + 9 + x 2 + 8 x + 16 + 3 x − 23 = 0 ⇔ 2 x 2 + 5 x + 2 = 0
Có a = 2; b = 5; c = 2 ⇒ Δ = 5 2 – 4 . 2 . 2 = 9 > 0
⇒ Phương trình có hai nghiệm:
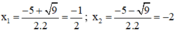
Vậy phương trình có tập nghiệm 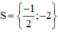
b)
x 3 + 2 x 2 − ( x − 3 ) 2 = ( x − 1 ) x 2 − 2 ⇔ x 3 + 2 x 2 − x 2 − 6 x + 9 = x 3 − x 2 − 2 x + 2 ⇔ x 3 + 2 x 2 − x 2 + 6 x − 9 − x 3 + x 2 + 2 x − 2 = 0 ⇔ 2 x 2 + 8 x − 11 = 0
Có a = 2; b = 8; c = -11 ⇒ Δ ’ = 4 2 – 2 . ( - 11 ) = 38 > 0
⇒ Phương trình có hai nghiệm:
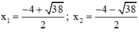
Vậy phương trình có tập nghiệm 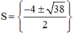
c)
( x − 1 ) 3 + 0 , 5 x 2 = x x 2 + 1 , 5 ⇔ x 3 − 3 x 2 + 3 x − 1 + 0 , 5 x 2 = x 3 + 1 , 5 x ⇔ x 3 + 1 , 5 x − x 3 + 3 x 2 − 3 x + 1 − 0 , 5 x 2 = 0 ⇔ 2 , 5 x 2 − 1 , 5 x + 1 = 0
Có a = 2,5; b = -1,5; c = 1
⇒ Δ = ( - 1 , 5 ) 2 – 4 . 2 , 5 . 1 = - 7 , 75 < 0
Vậy phương trình vô nghiệm.
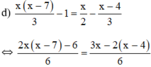
⇔ 2 x ( x − 7 ) − 6 = 3 x − 2 ( x − 4 ) ⇔ 2 x 2 − 14 x − 6 = 3 x − 2 x + 8 ⇔ 2 x 2 − 14 x − 6 − 3 x + 2 x − 8 = 0 ⇔ 2 x 2 − 15 x − 14 = 0
Có a = 2; b = -15; c = -14
⇒ Δ = ( - 15 ) 2 – 4 . 2 . ( - 14 ) = 337 > 0
⇒ Phương trình có hai nghiệm:
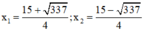
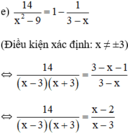
⇔ 14 = ( x - 2 ) ( x + 3 ) ⇔ 14 = x 2 - 2 x + 3 x - 6 ⇔ x 2 + x - 20 = 0
Có a = 1; b = 1; c = -20
⇒ Δ = 1 2 – 4 . 1 . ( - 20 ) = 81 > 0
Phương trình có hai nghiệm:
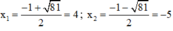
Cả hai nghiệm đều thỏa mãn điều kiện xác định.
Vậy phương trình có tập nghiệm S = {-5; 4}.
f) Điều kiện: x≠-1;x≠4

Ta có: a= 1, b = -7, c = - 8
∆ = ( - 7 ) 2 – 4 . 1 . ( - 8 ) = 81
=> Phương trình có hai nghiệm:
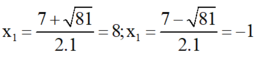
Kết hợp với diều kiện, nghiệm của phương trình đã cho là x = 8
Đúng 0
Bình luận (0)
Bài 1: Khai triển các hằng đẳng thức.
1,(x+1)2
2,(2x+1)2
3, (2x+y)2
4, (2x+3)2
5, ( 3x+2y)2
6, (2x2+1)2
7, (x3+1)2
8, (x2+y3)2
9, ( x2+2y2)2
10, (1/2x+1/3y)2
1) \(\left(x+1\right)^2=x^2+2x+1\)
2) \(\left(2x+1\right)^2=4x^2+4x+1\)
3) \(\left(2x+y\right)^2=4x^2+4xy+y^2\)
4) \(\left(2x+3\right)^2=4x^2+12x+9\)
5) \(\left(3x+2y\right)^2=9x^2+12xy+4y^2\)
6) \(\left(2x^2+1\right)^2=4x^4+4x^2+1\)
7) \(\left(x^3+1\right)^2=x^6+2x^3+1\)
8) \(\left(x^2+y^3\right)^2=x^4+2x^2y^3+y^6\)
9) \(\left(x^2+2y^2\right)^2=x^4+4x^2y^2+4y^4\)
10) \(\left(\dfrac{1}{2}x+\dfrac{1}{3}y\right)^2=\dfrac{1}{4}x^2+\dfrac{1}{3}xy+\dfrac{1}{9}y^2\)
Đúng 1
Bình luận (0)
Giải các phương trình sau:a)
1
−
x
2
+
x
+
2
2
2
x
x
−
3
−
7
;
b)
2
−
x...
Đọc tiếp
Giải các phương trình sau:
a) 1 − x 2 + x + 2 2 = 2 x x − 3 − 7 ;
b) 2 − x 3 − x − 4 3 = 8 x − 3 2 ;
c) 3 x − 1 4 + 6 x − 2 8 = 1 − 3 x 6 ;
d) x + 2 3 − x 5 12 = 1 + 1 − 9 − 2 x 12 5 .
a) Triển khai hằng đẳng thức và rút gọn được 8x + 12 = 0
Từ đó tìm được x = - 3 2
b) Sử dụng hằng đẳng thức, biến đổi phương trình về dạng: (x - 3)(2 x 2 - 4x) = 0
Sưe dụng phương pháp giải PT tích tìm được x ∈ {0; 2; 3}
c) Quy đồng khử mẫu ta được 48x - 16 = 0
Từ đó tìm được x = 1 3
d) Quy đồng khử mẫu ta được 3x + 6 = 2x + 63
Từ đó tìm được x = 57.
Đúng 0
Bình luận (0)