sử dụng hàm max , min với một cột nào đó sẽ cho kết quả là giá trị lớn nhất hay 1 giá trị nhỏ nhất trong cột đó , việc sử dụng hàm như thế có tương đương với sử dụng lệnh lọc ra 1 giá trị lớn nhất hay nhỏ nhất trong cột đó hay không
không hiểu cho lắm bạn à!! Dùng hàm max, min để tìm ra giá trị nhỏ nhất, lớn nhất trong bảng cho trước mà vẫn giữ nguyên cột cho trước còn lọc ra 1 giá trị lớn nhất hay nhỏ nhất thì nó sẽ bị mất số liệu của cột cho trước.
Đúng 0
Bình luận (0)
Viết chương trình nhập vào một mảng;
a. Viết hàm tìm vị trí phần tử lớn nhất trong mảng vừa nhập.
b. Viết hàm chèn phần tử có giá trị X vào phía sau phần tử có giá trị lớn nhất trong mảng.
c. In ra mảng sau khi chèn phần tử X
Lấy một ví dụ giải thích cho ý a., ý b.
Lập bảng biến thiên của hàm số \(y = {x^2} + 2x + 3.\) Hàm số này có giá trị lớn nhất hay giá trị nhỏ nhất? Tìm giá trị đó.
Tham khảo:
Đỉnh S có tọa độ: \({x_S} = \dfrac{{ - b}}{{2a}} = \dfrac{{ - 2}}{{2.1}} = - 1;\,{y_S} = {\left( { - 1} \right)^2} + 2.( - 1) + 3 = 2.\)
Hay \(S\left( { - 1;2} \right).\)
Vì hàm số bậc hai có \(a = 1 > 0\) nên ta có bảng biến thiên sau:
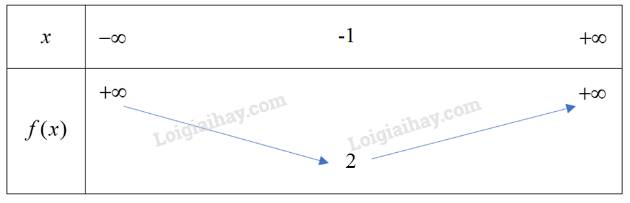
Hàm số đạt giá trị nhỏ nhất bằng \(2\).
Đúng 0
Bình luận (0)
Cách sử dụng các hàm để tính toán, hàm tính tổng, hàm tính trung bình cộng, hàm tìm giá trị lớn nhất, hàm tìm giá trị nhỏ nhất (SUM, AVERAGE, MAX, MIN)? ( trả lời giúp mình nhé !)
Hàm tính tổng:
=Sum(a,b,c,...)
Hàm tính trung bình cộng:
=average(a,b,c,...)
Đúng 1
Bình luận (0)
Cho hàm số
y
f
x
liên tục trên [-3;2] và có bảng biến thiên như sau. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
f
x
trên đoạn [-1;2]. Tính M + m. A. 3 B. 2 C. 1 D. 4
Đọc tiếp
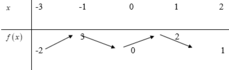
Cho hàm số y = f x liên tục trên [-3;2] và có bảng biến thiên như sau. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f x trên đoạn [-1;2]. Tính M + m.
A. 3
B. 2
C. 1
D. 4
Chọn A.
Phương pháp
Quan sát bảng biến thiên và tìm GTLN, GTNN của hàm số trên đoạn [-1;2] rồi kết luận.
Cách giải:
Quan sát bảng biến thiên ta thấy trên đoạn [-1;2] thì hàm số đạt GTNN bằng 0 tại x = 0 và đạt GTLN bằng 3 tại x = -1
![]()
Đúng 0
Bình luận (0)
Cho hàm số yf(x) có bảng xét dấu của đạo hàm như sauBiết rằng f(0)+f(3)f(2)+f(5) Giá trị nhỏ nhất, giá trị lớn nhất của hàm số f(x) trên đoạn [0;5] lần lượt là A. f(0), f(5) B. f(2), f(0) C. f(1), f(5) D. f(2), f(5)
Đọc tiếp
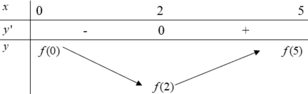
Cho hàm số y=f(x) có bảng xét dấu của đạo hàm như sau

Biết rằng f(0)+f(3)=f(2)+f(5) Giá trị nhỏ nhất, giá trị lớn nhất của hàm số f(x) trên đoạn [0;5] lần lượt là
A. f(0), f(5)
B. f(2), f(0)
C. f(1), f(5)
D. f(2), f(5)
Dựa vào bảng xét dấu của f '(x) ta có bảng biến thiên của hàm số trên đoạn [0;5] như sau
Suy ra ![]() Và
Và ![]()
Ta có ![]()
![]()
Vì f(x) đồng biến trên đoạn [2;5] nên ![]()
⇒ f(5)>f(0)
Vậy
![]()
Chọn đáp án D.
Đúng 0
Bình luận (0)
Cho bài toán: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
2
x
4
−
4
x
2
+
3
. Dưới đây là lời giải của học sinh:* Bước 1: Tập xác định DR. Đạo hàm
y
8
x
3
−
8
x
.* Bước 2: Cho
y
0
tìm .* Bướ...
Đọc tiếp
Cho bài toán: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 x 4 − 4 x 2 + 3 . Dưới đây là lời giải của học sinh:
* Bước 1: Tập xác định D=R. Đạo hàm y ' = 8 x 3 − 8 x .
* Bước 2: Cho y ' = 0 tìm .
* Bước 3: Tính y 0 = 3 ; y − 1 = y 1 = 1 . Vậy giá trị lớn nhất của hàm số là 3, và giá trị nhỏ nhất là 1.
Lời giải trên đúng hay sai? Nếu sai thì giải sai từ bước mấy?
A. Bước 2.
B. Lời giải đúng.
C. Bước 3.
D. Bước 1.
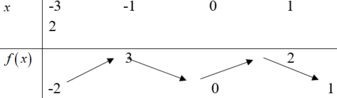
Cho hàm số y=f(x) liên tục trên [-3;2] và có bảng biến thiên như sau. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [-1;2]. Tính M + m.
A. 3
B. 2
C. 1
D. 4
Các chương trình bảng tính có công cụ để thực hiện tính toán theo các công thức được định nghĩa sẵn. Công cụ đó là?
A. Tính tổng B. tính giá trị lớn nhất.
C. Hàm. D. Phương trình
Xem thêm câu trả lời
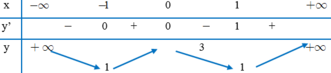
Hàm số
y
x
x
2
+
1
có giá trị lớn nhất là M, giá trị nhỏ nhất là m. Tính giá trị biểu thức
P
M
2
+
m
2
A.
P
1
4
B.
P
1
2
C....
Đọc tiếp
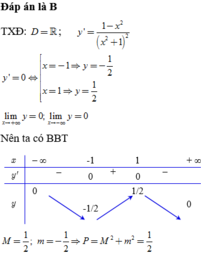
Hàm số y = x x 2 + 1 có giá trị lớn nhất là M, giá trị nhỏ nhất là m. Tính giá trị biểu thức P = M 2 + m 2
A. P = 1 4
B. P = 1 2
C. P = 2
D. P = 1