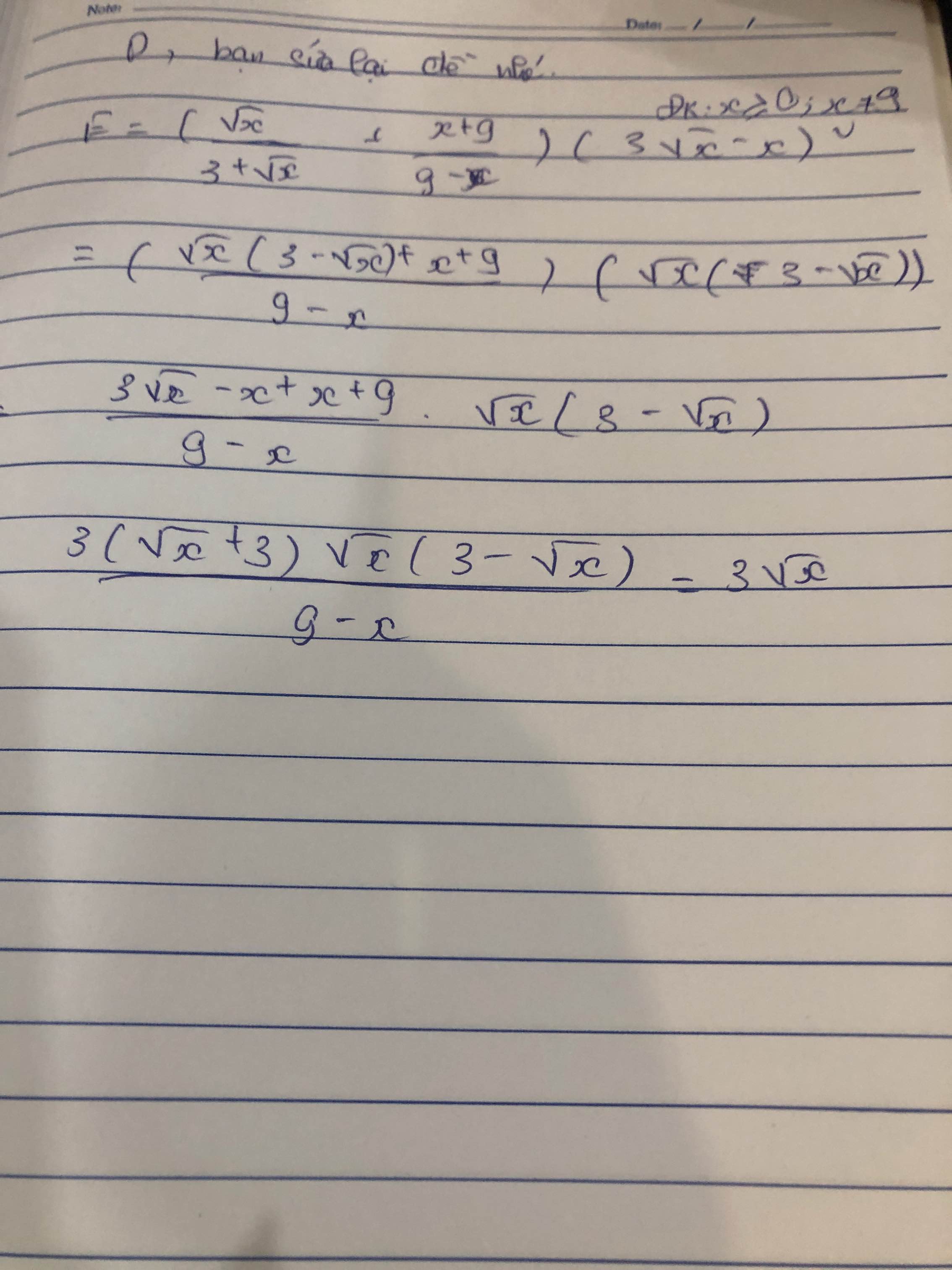1: ĐKXĐ: x+3>=0

=>x>=-3

\(\sqrt{x+3}>2\)

=>x+3>4

=>x>4-3=1

2: ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x< >4\end{matrix}\right.\)

\(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}< 1\)

=>\(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-1< 0\)

=>\(\dfrac{\sqrt{x}+1-\sqrt{x}+2}{\sqrt{x}-2}< 0\)

=>\(\dfrac{3}{\sqrt{x}-2}< 0\)

=>\(\sqrt{x}-2< 0\)

=>\(\sqrt{x}< 2\)

=>0<=x<4

3: ĐKXĐ: x>=0

\(\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)-5=\sqrt{x}\left(\sqrt{x}+2\right)-5\)

=>\(x-4\sqrt{x}+3-5=x+2\sqrt{x}-5\)

=>\(x-4\sqrt{x}-2-x-2\sqrt{x}+5=0\)

=>\(-6\sqrt{x}+3=0\)

=>\(-6\sqrt{x}=-3\)

=>\(\sqrt{x}=\dfrac{1}{2}\)

=>x=1/4(nhận)

\(\left(x^2+9\right)\left[x^2+9+9\left(y-1\right)\right]=22\left(y-1\right)^2\)

Đặt \(\left\{{}\begin{matrix}x^2+9=a\\y-1=b\end{matrix}\right.\)

\(\Rightarrow a\left(a+9b\right)=22b^2\Leftrightarrow a^2+9ab-22b^2=0\)

\(\Leftrightarrow\left(a-2b\right)\left(a+11b\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}a=2b\\a=-11b\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x^2+9=2\left(y-1\right)\\x^2+9=-11\left(y-1\right)\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x^2-2=2y-13\\x^2-2=-11y\end{matrix}\right.\) thay xuống dưới:

TH1: \(x^2-2=2y-13\Rightarrow2y-13=4y\sqrt{y+1}\)

Đặt \(\sqrt{y+1}=t\ge0\)

\(\Rightarrow2\left(t^2-1\right)-13=4t\left(t^2-1\right)\)

\(\Leftrightarrow4t^3-2t^2-4t+15=0\) (pt bậc 3 này ko giải được bằng kiến thức phổ thông :) )

TH2: \(x^2-2=-11y\Rightarrow-11y=4y\sqrt{y+1}\)

\(\Rightarrow y=0\Rightarrow x=\pm\sqrt{2}\)

Từ \(pt\left(1\right)\Leftrightarrow\left(x^2+11y-2\right)\left(x^2+2y-11\right)=0\)

Bạn thay vào giải là ra nhé

21: ĐKXĐ: x>0; x<>1

\(A=\left(\dfrac{x\sqrt{x}+1-\left(x-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\right):\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)+\sqrt{x}}{\sqrt{x}-1}\)

\(=\dfrac{x\sqrt{x}+1-x\sqrt{x}-x+\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}-1}{x}\)

\(=\dfrac{-x+\sqrt{x}+2}{\sqrt{x}+1}\cdot\dfrac{1}{x}\)

\(=\dfrac{-\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{x\left(\sqrt{x}+1\right)}=\dfrac{-\sqrt{x}+2}{x}\)

22:
DKXĐ: x>0; x<>1

\(A=\dfrac{x-\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}:\left(\dfrac{\sqrt{x}+1}{\sqrt{x}}+\dfrac{1}{\sqrt{x}-1}+\dfrac{2-x}{\sqrt{x}\left(\sqrt{x}-1\right)}\right)\)

\(=\dfrac{\sqrt{x}}{\sqrt{x}-1}:\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)+\sqrt{x}+2-x}{\sqrt{x}\left(\sqrt{x}-1\right)}\)

\(=\dfrac{\sqrt{x}}{\sqrt{x}-1}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{x-1+\sqrt{x}+2-x}\)

\(=\dfrac{x}{\sqrt{x}+1}\)

23: ĐKXĐ: x>0; x<>4

\(A=\dfrac{\sqrt{x}-4+3\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}:\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)-x}{\sqrt{x}\left(\sqrt{x}-2\right)}\)

\(=\dfrac{4\sqrt{x}-4}{\sqrt{x}\left(\sqrt{x}-2\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{-4}\)

\(=\dfrac{-4\sqrt{x}+4}{4}=-\sqrt{x}+1\)

24: ĐKXĐ: x>=0; x<>1

\(A=\dfrac{2x+1-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}:\dfrac{x+\sqrt{x}+1-x+2}{x+\sqrt{x}+1}\)

\(=\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{x+\sqrt{x}+1}{\sqrt{x}+3}\)

\(=\dfrac{\sqrt{x}}{\sqrt{x}+3}\)

25:

ĐKXĐ: x>=0; x<>1

\(A=1:\dfrac{x+2\sqrt{x}-2-\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)+x-\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)

\(=\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{2x+\sqrt{x}-1-x+1}\)

\(=\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{x+\sqrt{x}}=\dfrac{x-\sqrt{x}+1}{\sqrt{x}}\)

27: ĐKXĐ: x>0; x<>4

\(P=\dfrac{4\sqrt{x}\left(\sqrt{x}-2\right)-8}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}:\dfrac{\sqrt{x}-1-2\left(\sqrt{x}-2\right)}{\sqrt{x}\left(\sqrt{x}-2\right)}\)

\(=\dfrac{4x-8\sqrt{x}-8}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{x-1-2\sqrt{x}+1}\)

\(=\dfrac{4\left(x-2\sqrt{x}-2\right)}{\sqrt{x}+2}\cdot\dfrac{\sqrt{x}}{-\sqrt{x}}\)

\(=\dfrac{-4\left(x-2\sqrt{x}-2\right)}{\sqrt{x}+2}\)

\(A=\left(\frac{x}{\sqrt{x}-1}-\sqrt{x}\right):\left(\frac{\sqrt{x}+1}{\sqrt{x}}-\frac{1}{1-\sqrt{x}}+\frac{2-x}{x-\sqrt{x}}\right)\)

\(=\frac{x-x+\sqrt{x}}{\sqrt{x}-1}:\frac{x-1+\sqrt{x}+2-x}{\sqrt{x}\left(\sqrt{x}-1\right)}\)

\(=\frac{\sqrt{x}}{\sqrt{x}-1}.\frac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}+1}=\frac{x}{\sqrt{x}+1}\)

c) \(\sqrt[]{8+\sqrt[]{x}}+\sqrt{5-\sqrt[]{x}}=5\)

\(\Leftrightarrow\left(\sqrt[]{8+\sqrt[]{x}}+\sqrt{5-\sqrt[]{x}}\right)^2=25\left(1\right)\left(đkxđ:0\le x\le25\right)\)

Áp dụng Bất đẳng thức Bunhiacopxki cho 2 cặp số dương \(\left(1;\sqrt[]{8+\sqrt[]{x}}\right);\left(1;\sqrt{5-\sqrt[]{x}}\right)\)

\(\left(1.\sqrt[]{8+\sqrt[]{x}}+1.\sqrt{5-\sqrt[]{x}}\right)^2\le\left(1^2+1^2\right)\left(8+\sqrt[]{x}+5-\sqrt[]{x}\right)=26\)

\(\left(1\right)\Leftrightarrow26=25\left(vô.lý\right)\)

Vậy phương trình đã cho vô nghiệm

b) \(\sqrt[]{1+4x}+2\sqrt[]{2-x}+2\sqrt[]{\left(1+4x\right)\left(2-x\right)}=3\)  \(\left(đkxđ:-\dfrac{1}{4}\le x\le2\right)\)

\(\)\(\Leftrightarrow\sqrt[]{1+4x}+2\sqrt[]{2-x}=3-2\sqrt[]{\left(1+4x\right)\left(2-x\right)}\)

\(\Leftrightarrow\left(\sqrt[]{1+4x}+2\sqrt[]{2-x}\right)^2=\left[3-2\sqrt[]{\left(1+4x\right)\left(2-x\right)}\right]^2\left(1\right)\)

Áp dụng Bất đẳng thức Bunhiacopxki :

\(\left(1.\sqrt[]{1+4x}+2\sqrt[]{2-x}\right)^2\le\left(1^2+2^2\right)\left(1+4x+2-x\right)=5\left(3x+3\right)\)

Áp dụng Bất đẳng thức Cauchy :

\(2\sqrt[]{\left(1+4x\right)\left(2-x\right)}\le1+4x+2-x=3x+3\)

Dấu "=" xảy ra khi và chỉ khi

\(1+4x=2-x\)

\(\Leftrightarrow x=\dfrac{1}{5}\left(thỏa.đk\right)\)

\(pt\left(1\right)\Leftrightarrow5\left(4x+3\right)=4x+3\)

\(\Leftrightarrow4\left(4x+3\right)=0\)

\(\Leftrightarrow x=-\dfrac{3}{4}\left(k.thỏa.x=\dfrac{1}{5}.vô.lý\right)\)

Vậy phương trình đã cho vô nghiệm