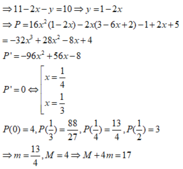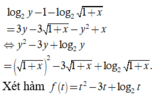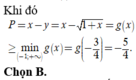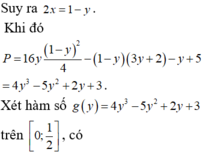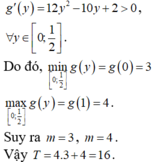Cho x+3y>=1 . Giá trị nhỏ nhất của biểu thức là A=x^2+y^2

Những câu hỏi liên quan
Cho hai số thực
x
,
y
thỏa mãn
0
≤
x
≤
1
2
,
0
y
≤
1
và
log
(
11
-
2
x
-
y
)
2
x
+
4
y
-
1
...
Đọc tiếp
Cho hai số thực x , y thỏa mãn 0 ≤ x ≤ 1 2 , 0 < y ≤ 1 và log ( 11 - 2 x - y ) = 2 x + 4 y - 1 Xét biểu thức P = 16 x 2 y - 2 x ( 3 y + 2 ) - y + 5 . Gọi m , M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của P. Khi đó giá trị của biểu thức T = 4 m + M bằng bao nhiêu?
A. 16
B. 18
C. 17
D. 19
Cho \(x+3y\ge1.\)Giá trị nhỏ nhất của biểu thức \(A=x^2+y^2\) là ?
Ta có: \(x\ge3y-1\) (gt).
\(\Rightarrow A=x^2+y^2\ge\left(3y-1\right)^2+y^2=9y^2-6y+1+y^2=10y^2-6y+1=10\left(y-\frac{3}{10}\right)^2+\frac{1}{10}\)
\(\Rightarrow A\ge\frac{1}{10}\Rightarrow GTNN\left(A\right)=10\)
Dấu "=" xảy ra khi \(y=\frac{3}{10};x=\frac{1}{10}\).
Đúng 0
Bình luận (0)
Sửa giùm mình lại chỗ: \(x\ge1-3y\) nha, mình viết nhầm.
Đúng 0
Bình luận (0)
Vs GTNN của A=1/10 không phải là 10
Đúng 0
Bình luận (0)
cho x,y > 0 và 2x+y ≥ 7 tính giá trị nhỏ nhất của biểu thức
P = \(x^2-x+3y+\dfrac{9}{x}+\dfrac{1}{9}+9\)
Câu 15: ( 1.5 điểm)
a) Tìm giá trị nhỏ nhất của biểu thức:
A = ( 2x - 3y+1)2 + ( 2 + y) 2 - 12x + 2020
b) Chứng minh biểu thức sau có giá trị không phụ thuộc vào giá trị của biến:
B = ( x - 2y)(x2 + 2xy + 4y2) - x ( x + 2)(x - 2) - 4x + 8y3 + 2021
b: \(B=x^3-8y^3-x^3+4x-4x+8y^3+2021=2021\)
Đúng 1
Bình luận (0)
Phân tích đa thức sau thành phân tử
a, 4x³ - 10x² + 2x
b, x² - 3x + 2
Giúp mk vs m.n
Đúng 0
Bình luận (1)
Hình thang ABCD (AB//CD) có các tia phân giác của các góc A và D gặp nhau tại điểm E thuộc cạnh BC. Chứng minh rằng:
a, AED = 90°
b, AD = AB + CD
Giúp mình với mọi người :(((
Đúng 0
Bình luận (0)
Cho các số thực x; y thõa mãn x≥0; y≥0 và x+y1. Giá trị lớn nhất M , giá trị nhỏ nhất m của biểu thức
S
(
4
x
2
+
3
y
)
(
4
y
2
+
3
x
)
+
25
x
y
là: A.
M
25
2
;
m...
Đọc tiếp
Cho các số thực x; y thõa mãn x≥0; y≥0 và x+y=1. Giá trị lớn nhất M , giá trị nhỏ nhất m của biểu thức S = ( 4 x 2 + 3 y ) ( 4 y 2 + 3 x ) + 25 x y là:
A. M = 25 2 ; m = 191 16 .
B. M = 12 ; m = 191 16 .
C. M = 25 2 ; m = 12 .
D. M = 25 2 ; m = 0 .
Do x+ y= 1 nên
S = 16 x 2 y 2 + 12 ( x + y ) ( x 2 - x y + y 2 ) + 34 x y = 16 x 2 y 2 + 12 ( x + y ) 2 - 3 x y + 34 x y , d o x + y = 1 = 16 x 2 y 2 - 2 x y + 12
Đặt t= xy . Do x≥ 0 ; y≥0 nên
0 ≤ x y ≤ ( x + y ) 2 4 = 1 4 ⇒ t ∈ 0 ; 1 4
Xét hàm số f(t) = 16t2- 2t + 12 trên [0 ; 1/4].
Ta có f’ (t) = 32t- 2 ; f’(t) =0 khi t= 1/ 16 .
Bảng biến thiên
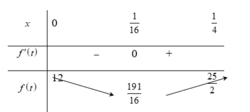
Từ bảng biến thiên ta có:
m i n 0 ; 1 4 f ( t ) = f ( 1 16 ) = 191 16 ; m a x 0 ; 1 4 f ( t ) = f ( 1 4 ) = 25 2
Vậy giá trị lớn nhất của S là 25/2 đạt được khi
x + y = 1 x y = 1 4 ⇔ x = 1 2 y = 1 2
giá trị nhỏ nhất của S là 191/ 16 đạt được khi
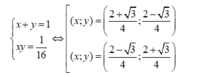
Chọn A.
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức A=x^2 +xy +y^2 -3x -3y
Cho x, y là các số thực thỏa mãn
log
2
y
2
1
+
x
3
y
-
1
+
x
-
y
2
+
x
. Giá trị nhỏ nhất của biểu thức
P
x...
Đọc tiếp
Cho x, y là các số thực thỏa mãn log 2 y 2 1 + x = 3 y - 1 + x - y 2 + x . Giá trị nhỏ nhất của biểu thức P = x - y bằng
A. - 3 4
B. - 5 4
C. -2
D. -1
Cho hai số thực x,y thỏa mãn
0
≤
x
≤
1
2
,
0
≤
y
≤
1
2
, và
log
(
11
-
2
x
-
y
)
2...
Đọc tiếp
Cho hai số thực x,y thỏa mãn 0 ≤ x ≤ 1 2 , 0 ≤ y ≤ 1 2 , và log ( 11 - 2 x - y ) = 2 y + 4 x - 1 . Xét biểu thức P = 16 y x 2 - 2 x ( 3 y + 2 ) - y + 5 . Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của P. Khi đó giá trị của T = ( 4 m + M ) bằng bao nhiêu?
A. 16
B. 18
C. 17
D. 19
mình cần gấp mong mn giải cho mình nhanh
1. tìm giá trị nhỏ nhất của biểu thức
A= (x+3)2+(x-5)2
2. tìm giá trị lớn nhất của biểu thức
A= x2+y2 với x+3y=10
Bài 1:
\(A=x^2+6x+9+x^2-10x+25\)
\(=2x^2+4x+34\)
\(=2\left(x^2+2x+17\right)\)
\(=2\left(x+1\right)^2+32>=32\forall x\)
Dấu '=' xảy ra khi x=-1
Đúng 1
Bình luận (1)