Chứng tỏ rằng: 1/3^3 + 1/5^3 + 1/7^3 +..+ 1/2021^3 < 1/12

Những câu hỏi liên quan
1)Chứng minh rằng: 4n + 7/6n +1 là phân số tối giản
2) Cho A=1-1/2+1/3-1/4+...+1/99-1/100
Chứng tỏ:7/12<A<5/6
Làm ơn giải ra giúp mình nha :-)
Gọi d là ƯC của 4n + 7 và 6n + 1
Khi đó : 4n + 7 chia hết cho d và 6n + 1 chia hết cho d
<=> 12n + 21 chia hết cho d và 12n + 2 chia hết cho d
=> (12n + 21) - ( 12n + 2) chia hết cho d = > 19 chia hết cho d
Vì 19 là số nguyên tố => d = 1
Vậy \(\frac{4n+7}{6n+1}\) Là p/s tối giản
Đúng 0
Bình luận (0)
Nếu n = 3 thì 4n+7/6n+1=1 đâu phải là phân số tối giản
Đúng 0
Bình luận (0)
Chứng tỏ rằng A là số chính phương biết A=1+3+5+7+9+11+....+(2n-1)
Chứng tỏ rằng
1/2×3/4×5/6×7/8×……×99/100<1/10
1/Chứng tỏ 77 là ước của A=76+75-74
2/Cho A=2+22+23+...+260.Chứng tỏ rằng A là bội của 3, của 7 và của 15
3/Cho B=1+5+52+53+...+596+597+598. Chứng tỏ B chia hết cho 31
Bài 5 : Chứng tỏ rằng :
1/2 + 1/3 + 1/4 + ...+ 1/63 > 2
chứng minh rằng: 1/3 + 1/3 mũ 2 + 1/3 mũ 3 + ... + 1/3 mũ 2021
Chứng minh rằng :
\(2021-\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}\right)=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+...+\dfrac{2020}{2021}\)
\(2021-\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}\right)\)
\(=\left(1-1\right)+\left(1-\dfrac{1}{2}\right)+\left(1-\dfrac{1}{3}\right)+...+\left(1-\dfrac{1}{2021}\right)\)
\(=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+...+\dfrac{2020}{2021}\)
Đúng 1
Bình luận (0)
Giải:
\(2021-\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}\right)=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+...+\dfrac{2020}{2021}\)
Ta có:
\(2021-\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}\right)\)
\(=\left(1-1\right)+\left(1-\dfrac{1}{2}\right)+\left(1-\dfrac{1}{3}\right)+...+\left(1-\dfrac{1}{2021}\right)\)
\(=0+\dfrac{1}{2}+\dfrac{2}{3}+...+\dfrac{2020}{2021}\)
\(=\dfrac{1}{2}+\dfrac{2}{3}+...+\dfrac{2020}{2021}\)
Mà \(\dfrac{1}{2}+\dfrac{2}{3}+...+\dfrac{2020}{2021}=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+...+\dfrac{2020}{2021}\)
\(\Rightarrow2021-\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}\right)=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+...+\dfrac{2020}{2021}\left(đpcm\right)\)
Đúng 0
Bình luận (0)
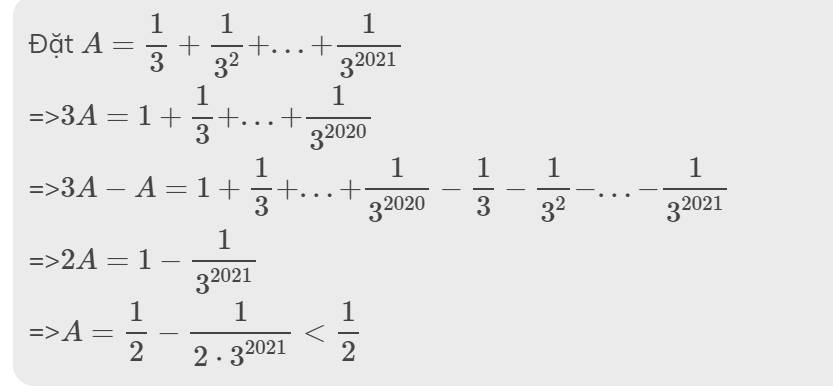
chứng minh rằng: 1/3 + 1/3 mũ 2 + 1/3 mũ 3 + ... + 1/3 mũ 2021<1/2
Đặt \(A=\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{2021}}\)
=>\(3A=1+\dfrac{1}{3}+...+\dfrac{1}{3^{2020}}\)
=>\(3A-A=1+\dfrac{1}{3}+...+\dfrac{1}{3^{2020}}-\dfrac{1}{3}-\dfrac{1}{3^2}-...-\dfrac{1}{3^{2021}}\)
=>\(2A=1-\dfrac{1}{3^{2021}}\)
=>\(A=\dfrac{1}{2}-\dfrac{1}{2\cdot3^{2021}}< \dfrac{1}{2}\)
Đúng 3
Bình luận (2)
Chứng tỏ rằng:
\(A=\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\frac{1}{5^2}+\frac{1}{6^2}+\frac{1}{7^2}< 1\)
Ta có \(A=\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\frac{1}{5^2}+\frac{1}{6^2}+\frac{1}{7^2}< \frac{1}{1\cdot2}+\frac{1}{2\cdot3}+\frac{1}{3\cdot4}+\frac{1}{4\cdot5}+\frac{1}{5\cdot6}+\frac{1}{7\cdot8}\)
\(\Rightarrow A< 1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-....+\frac{1}{7}-\frac{1}{8}\)
\(\Rightarrow A< 1-\frac{1}{8}< 1\)