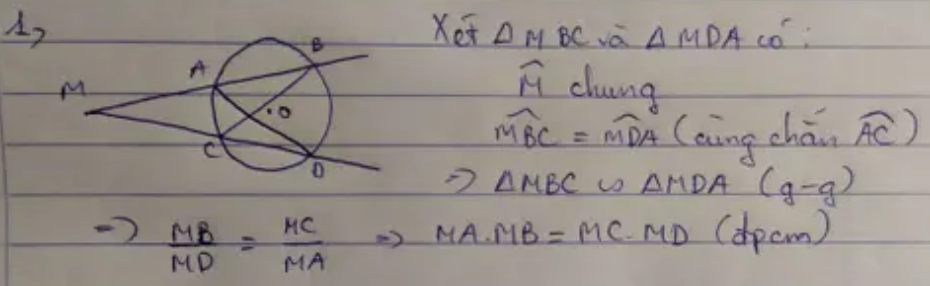Cho (O) có 2 cát tuyến MAB và MCD. Cm MA.Mb=MC.MD

Những câu hỏi liên quan
cho đường tròn tâm O bán kính R. Điểm M nằm ngoài đường tròn, vẽ cát tuyến MAB và MCD. CM: MA.MB = MC.MD
Xét ΔMBC và ΔMDA có
góc MBC=góc MDA
góc DMA chung
=>ΔMBC đồng dạng với ΔMDA
=>MB/MD=MC/MA
=>MB*MA=MD*MC
Đúng 0
Bình luận (0)
Từ điểm M nằm ngoài (O) vẽ 2 cát tuyến MAB và MCD
a) CM: tam giác MAD đồng dạng với tam giác MCD
b) MA.MB=MC.MD
a: Xét ΔMAD và ΔMCB có
\(\widehat{M}\) chung
\(\widehat{MDA}=\widehat{MBC}\)
Do đó: ΔMAD∼ΔMCB
b: Ta có: ΔMAD∼ΔMCB
nên \(\dfrac{MA}{MC}=\dfrac{MD}{MB}\)
hay \(MA\cdot MB=MC\cdot MD\)
Đúng 2
Bình luận (0)
a)Xét (O) có:
ADC và ABC là 2 góc nội tiếp cùng chắn cung AC
=> góc ADC = góc ABC hay góc MDA = góc MBC
Xét tam giác MAD và tam giác MCB có :
Góc M chung
góc MDA= góc MBC(cmt)
Vậy 2 tam giác trên đồng dạng(g.g)
b)Từ 2 tg trên đồng dạng
=>\(\dfrac{MD}{MB}=\dfrac{MA}{MC}\)
=>MA.MB=MC.MD
Đúng 1
Bình luận (0)
1/ Từ điểm M cố định nằm trong hoặc ngoài đường tròn (O) kẻ 2 cát tuyến bất kì MAB và MCD tới đường tròn
chứng minh: MA.MB=MC.MD
2/ Cho tam giác ABC nội tiếp đường tròn (O;R). tính độ dài cạnhBC theo R biết góc A = 45độ
ghi lại đầu bài cho rỏ đi mk giải cho đọc đàu bại của bạn ghi sai khó hiểu
Đúng 0
Bình luận (0)
ukm cố lên sắp thi lớp 10 chắc vật vã lắm nhỉ ^^
Đúng 0
Bình luận (0)
Từ điểm M nằm ngoài (O) kẻ hai cát tuyến MAB,MCD.
a) Chứng minh MA.MB = MC.MD
b) AD cắt BC tại N .Chứng minh NA.ND = NB.NC
c) Kẻ tiếp tuyến MP . Chứng minh MP2 = MA.MB = MC.MD
cho (O) và điểm M nằm ngoài đường tròn qua M kẻ tiếp tuyến MI và cát tuyến MCD với (O). CM MI^2 = MC.MD
Xét hai tam giác IMC và DMI có:
\(\left\{{}\begin{matrix}\widehat{IDM}\text{ chung}\\\widehat{CIM}=\widehat{IDM}\left(\text{góc nội tiếp và góc tiếp tuyến cùng chắn cung IM}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta IMC\sim\Delta DMI\) (g.g)
\(\Rightarrow\dfrac{MI}{DM}=\dfrac{MC}{MI}\Rightarrow MI^2=MC.MD\) (đpcm)
Đúng 0
Bình luận (0)
a) Từ một điểm M ở bên ngoài đường tròn left(O;Rright)kẻ tiếp tuyến MT và hai cát tuyến MAB và MCD với đường tròn (O) left(A,B,C,Dinleft(Oright)right). Chứng minh MA.MBMC.MDMT^2OM^2-R^2b) Qua điểm M ở bên trong đường tròn left(O;Rright)kẻ hai dây cung AB và CD của đường tròn (O) left(A,B,C,Dinleft(Oright)right).Chứng minhMA.MBMC.MDR^2-OM^2
Đọc tiếp
a) Từ một điểm M ở bên ngoài đường tròn \(\left(O;R\right)\)kẻ tiếp tuyến MT và hai cát tuyến MAB và MCD với đường tròn (O) \(\left(A,B,C,D\in\left(O\right)\right)\). Chứng minh \(MA.MB=MC.MD=MT^2=OM^2-R^2\)
b) Qua điểm M ở bên trong đường tròn \(\left(O;R\right)\)kẻ hai dây cung AB và CD của đường tròn (O) \(\left(A,B,C,D\in\left(O\right)\right).\)Chứng minh\(MA.MB=MC.MD=R^2-OM^2\)
Từ M ngoài (O) vẽ cát tuyến MAB và MCD, sđ cung AC=60 độ, sđ cung BD= 180 độ. Cho AD cắt BC tại I
a) tính góc AIC và góc M
b) C/m MA.MB=MC.MD
vẽ hình giúp với
a: Xét (O) có
\(\widehat{AMC}\) là có đỉnh ở bên ngoài đường tròn chắn hai cung AC và BD
=>\(\widehat{AMC}=\dfrac{1}{2}\cdot\left(sđ\stackrel\frown{BD}-sđ\stackrel\frown{AC}\right)=\dfrac{1}{2}\left(180^0-60^0\right)=60^0\)
Xét (O) có
ΔBAD nội tiếp
BD là đường kính
Do đó: ΔBAD vuông tại A
=>DA\(\perp\)MB tại A
Xét (O) có
ΔCBD nội tiếp
BD là đường kính
Do đó: ΔCBD vuông tại C
=>BC\(\perp\)MD tại C
Xét tứ giác MAIC có \(\widehat{MAI}+\widehat{MCI}+\widehat{AMC}+\widehat{AIC}=360^0\)
=>\(\widehat{AIC}+60^0+90^0+90^0=360^0\)
=>\(\widehat{AIC}=120^0\)
b: Xét ΔMCB vuông tại C và ΔMAD vuông tại A có
\(\widehat{M}\) chung
Do đó: ΔMCB~ΔMAD
=>\(\dfrac{MC}{MA}=\dfrac{MB}{MD}\)
=>\(MA\cdot MB=MC\cdot MD\)
Đúng 1
Bình luận (0)
Bài 5: Từ điểm M nằm ngoài đường tròn (O), kẻ tiếp tuyến MA và cát tuyến MCD sao cho MD nằm giữa hai tia MA và MO. a)Cm: MA?= MC.MD b)Vẽ dây AB vuông góc với OM tại H. Cm: MB là tiếp tuyến của đường tròn (O) c)Cm: MH.MO = MC.MD và MHC = MDÒ
GIÚP MÌNH VỚI MỌI NGƯỜI 😢
a) Cho đường tròn ( O ) và điểm E nằm ngoài đường tròn. Qua điểm E kẻ tiếp p tuyến ET và cắt tiếp tuyến EAB . Cm ET2 = EA . EB
b ) Cho đường tròn ( O ) và điểm M nằm ngoài đường tròn. Qua điểm M kẻ cắt hai tiếp tuyến MAB và MCD. Cm MA.MB = MC.MD