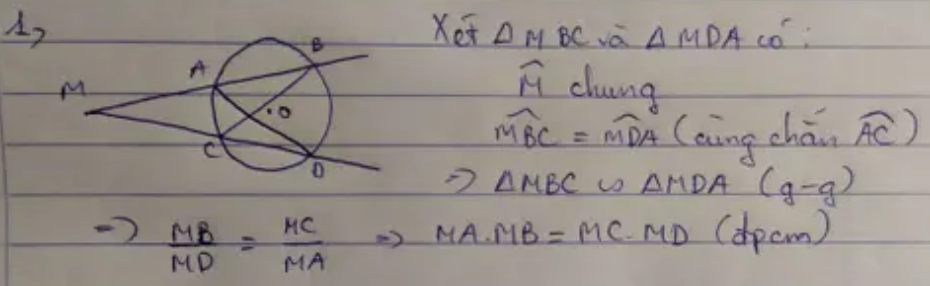a: Xét ΔMAD và ΔMCB có
\(\widehat{M}\) chung
\(\widehat{MDA}=\widehat{MBC}\)
Do đó: ΔMAD∼ΔMCB
b: Ta có: ΔMAD∼ΔMCB
nên \(\dfrac{MA}{MC}=\dfrac{MD}{MB}\)
hay \(MA\cdot MB=MC\cdot MD\)
a)Xét (O) có:
ADC và ABC là 2 góc nội tiếp cùng chắn cung AC
=> góc ADC = góc ABC hay góc MDA = góc MBC
Xét tam giác MAD và tam giác MCB có :
Góc M chung
góc MDA= góc MBC(cmt)
Vậy 2 tam giác trên đồng dạng(g.g)
b)Từ 2 tg trên đồng dạng
=>\(\dfrac{MD}{MB}=\dfrac{MA}{MC}\)
=>MA.MB=MC.MD