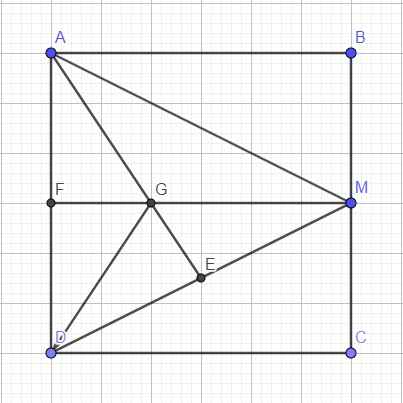
cho hình vuông ABCD có cạnh bằng 3. I là trung điểm AB. Tích vecto BI.CA

Những câu hỏi liên quan
Cho hình vuông ABCD có cạnh bằng a. Gọi M, N tương ứng là trung điểm của các cạnh AB, BC.
a) Biểu thị các vecto \(\overrightarrow {DM} ,\overrightarrow {AN} \) theo các vecto \(\overrightarrow {AB} ,\overrightarrow {AD} \)
b) Tính \(\overrightarrow {DM} .\overrightarrow {AN} \) và tìm góc giữa hai đường thẳng DM và AN.
a) Ta có:
\(\overrightarrow {DM} = \overrightarrow {DA} + \overrightarrow {AM} = - \overrightarrow {AD} + \frac{1}{2}\overrightarrow {AB} \) (do M là trung điểm của AB)
\(\overrightarrow {AN} = \overrightarrow {AB} + \overrightarrow {BN} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {BC} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} \) (do N là trung điểm của BC)
b)
\(\begin{array}{l}\overrightarrow {DM} .\overrightarrow {AN} = \left( { - \overrightarrow {AD} + \frac{1}{2}\overrightarrow {AB} } \right).\left( {\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} } \right)\\ = - \overrightarrow {AD} .\overrightarrow {AB} - \frac{1}{2}{\overrightarrow {AD} ^2} + \frac{1}{2}{\overrightarrow {AB} ^2} + \frac{1}{4}\overrightarrow {AB} .\overrightarrow {AD} \end{array}\)
Mà \(\overrightarrow {AB} .\overrightarrow {AD} = \overrightarrow {AD} .\overrightarrow {AB} = 0\) (do \(AB \bot AD\)), \({\overrightarrow {AB} ^2} = A{B^2} = {a^2};{\overrightarrow {AD} ^2} = A{D^2} = {a^2}\)
\( \Rightarrow \overrightarrow {DM} .\overrightarrow {AN} = - 0 - \frac{1}{2}{a^2} + \frac{1}{2}{a^2} + \frac{1}{4}.0 = 0\)
Vậy \(DM \bot AN\) hay góc giữa hai đường thẳng DM và AN bằng \({90^ \circ }\).
Đúng 0
Bình luận (0)
Giúp tui :v
Bài 1 : Cho hình chữ nhật ABCD có AB = 2a,AD = a.Tính độ dài vecto AB + vecto DB
Bài 2 : Cho tam giác ABC gọi I là trung điểm trên cạnh BC sao cho 2CI=3BJ,J trên cạnh BC sao cho 5BJ=2CI.Phân tích vecto AI và AJ theo hai vecto AB,AC
Bài 1:
Gọi M là trung điểm của AD
\(BM=\sqrt{AB^2+AM^2}=\sqrt{4a^2+\dfrac{1}{4}a^2}=\dfrac{\sqrt{17}}{2}a\)
\(\left|\overrightarrow{AB}+\overrightarrow{DB}\right|=2\cdot BM=\sqrt{17}a\)
Đúng 2
Bình luận (0)
Cho hình vuông ABCD có cạnh bằng 12 cm.
a, Tính diện tích hình vuông ABCD
b,Gọi M , N là trung điểm của AB và BC . I là giao điểm của MC và ND . Tính diện tích tam giác INC
a ) Diện tích hình vuông ABCD là :
12 x 12 = 144 (cm2)
Đúng 1
Bình luận (0)
a diện tích ABCD là
12x12=144[cm2]
Đúng 0
Bình luận (0)
b ) Có : N là trung điểm của BC => NB=NC = \(\frac{1}{2}\)x BC =6 ( cm)
Diện tích hình tam giác INC là :
(6x12):2 = 36
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hình thang vuông ABCD có AB bằng 12 cm, DC = 20 cm, AB bằng 16 cm, biết M là trung điểm của cạnh AB, N là trung điểm của cạnh BC. Tính diện tích hình thang ABNM và diện tích hình thang MNCD
cho hình chữ nhật ABCD. F là trung điểm của cạnh CD,E là điểm xác định bởi AB = 2EA.Gọi G là trọng tâm tam giác BEF.Phân tích vecto DG theo hai vecto AB,AD
Gọi M là trung điểm EF
\(\overrightarrow{BM}=\dfrac{1}{2}\overrightarrow{BE}+\dfrac{1}{2}\overrightarrow{BF}=-\dfrac{3}{2}\overrightarrow{AB}+\dfrac{1}{2}\left(\overrightarrow{BC}+\overrightarrow{CF}\right)\)
\(=-\dfrac{3}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}-\dfrac{1}{4}\overrightarrow{AB}=-\dfrac{7}{4}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\)
\(\overrightarrow{BG}=\dfrac{2}{3}\overrightarrow{BM}=-\dfrac{7}{6}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AD}\)
\(\overrightarrow{AG}=\overrightarrow{AB}+\overrightarrow{BG}=-\dfrac{1}{6}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AD}\)
\(\overrightarrow{DG}=\overrightarrow{DA}+\overrightarrow{AG}=-\overrightarrow{AD}+\overrightarrow{AG}=-\dfrac{1}{6}\overrightarrow{AB}-\dfrac{2}{3}\overrightarrow{AD}\)
Đúng 0
Bình luận (0)
Cho hình thoi abcd Tâm o cạnh a góc BAD Bằng 60 °. Gọi I J lần lượt là trung điểm AB , CD Và K Là trung điểm của I J.
a. CMR: Ka + Kb + Kc + Kd = 0
b. Tính độ dài Vecto AB + AD
Cho hình chóp S.ABCD có cạnh đáy ABCD là hình vuông tâm O cạnh bằng a, SA vuông góc với (ABCD) và SA 2a. Gọi I là trung điểm của SC và M là trung điểm của DC. Tính thể tích của khối chóp I.OBM. A.
a
3
24
B.
3
a
3
24
C.
a...
Đọc tiếp
Cho hình chóp S.ABCD có cạnh đáy ABCD là hình vuông tâm O cạnh bằng a, SA vuông góc với (ABCD) và SA = 2a. Gọi I là trung điểm của SC và M là trung điểm của DC. Tính thể tích của khối chóp I.OBM.
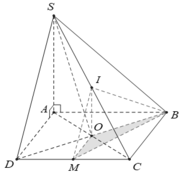
A. a 3 24
B. 3 a 3 24
C. a 3 3 24
D. a 3 2 24
Cho hình vuông ABCD có độ dài cạnh bằng 6. Gọi M là trung điểm của BC và G là trọng tâm tam giác ADM. Tính độ dài vecto GD
\(\left\{{}\begin{matrix}AM=\sqrt{AB^2+BM^2}=3\sqrt{5}\\DM=\sqrt{CD^2+CM^2}=3\sqrt{5}\end{matrix}\right.\) \(\Rightarrow\) tam giác ADM cân tại M
Gọi F là trung điểm AD \(\Rightarrow ABMF\) là hình chữ nhật \(\Rightarrow MF=AB=6\)
Theo tính chất trọng tâm: \(GF=\dfrac{1}{3}MF=2\)
\(DF=\dfrac{1}{2}AD=3\)
Đặt \(T=\left|\overrightarrow{GD}\right|=\left|\overrightarrow{GF}+\overrightarrow{FD}\right|\)
\(\Rightarrow T^2=GF^2+FD^2+2\overrightarrow{GF}.\overrightarrow{DF}=GF^2+DF^2=2^2+3^2=13\)
\(\Rightarrow\left|\overrightarrow{GD}\right|=\sqrt{13}\)
Đúng 2
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA ⊥ (ABCD) và SA a. Gọi E là trung điểm của cạnh AB. Diện tích mặt cầu ngoại tiếp hình chóp bằng .SBCE A.
14
πa
2
B.
11
πa
2
C.
8
πa
2
D.
12
πa
2
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA ⊥ (ABCD) và SA = a. Gọi E là trung điểm của cạnh AB. Diện tích mặt cầu ngoại tiếp hình chóp bằng .SBCE
A. 14 πa 2
B. 11 πa 2
C. 8 πa 2
D. 12 πa 2
Đáp án A
Phương pháp:
Sử dụng phương pháp tọa độ hóa.
Cách giải:
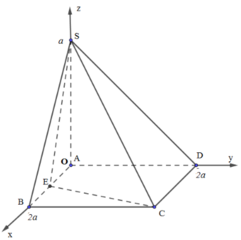
Gắn hệ trục tọa độ như hình vẽ.
Trong đó, B(2a;0;0), C(2a;2a;0), E(a;0;0), S(0;0;a)
Gọi I(x0;y0;z0) là tâm của mặt cầu ngoại tiếp hình chóp S.BEC. Khi đó, IS2 = IB2 = IC2 = IE2
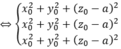
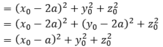
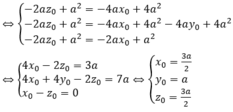
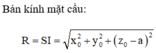
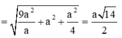
![]()
Đúng 0
Bình luận (0)