Cho tam giác ABC, I là trung điểm BC. Tìm tập hợp điểm M thỏa mãn \(\mid MA = \mid MB + MC \mid \)

Những câu hỏi liên quan
cho tam giác ABC. Tìm tập hợp điểm M thỏa mãn |MA +MB+ MC|=1
Cho tam giác ABC. Tập hợp các điểm M trong mặt phẳng thỏa mãn
M
A
;
→
M
B
→
;
M
C
→...
Đọc tiếp
Cho tam giác ABC. Tập hợp các điểm M trong mặt phẳng thỏa mãn M A ; → M B → ; M C → = M A → + 2 M B → - M C → là
A. một đoạn thẳng
B. một đường thẳng
C. một đường tròn
D. một elip
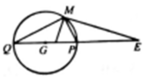
Chọn C.
Gọi G là trọng tâm tam giác ABC và E là điểm thỏa mãn E A → + 2 E B → - E C → = 0
(điểm E như thế luôn tồn tại duy nhất). Khi đó đẳng thức trên tương đương với 3 M G → = M E → hay 3 M G = M E . Trên đường thẳng GE ta lấy 2 điểm P, Q thỏa mãn 3 P G = P E = 3 Q G = Q E . Khi đó quỹ tích điểm M thỏa mãn yêu cầu là đường tròn đường kính PQ.
Đúng 0
Bình luận (0)
Cho tam giác ABC. Tìm tập hợp các điểm M thỏa mãn điều kiện (MA + MB) (MC - MB) = 0
(MA+MB)(MC-MB)=0 => MC-MB=0 => MB=MC
=> tg MBC cân tại M
Từ M dựng đường thẳng d vuông góc với BC => d là đường cao của tg cân MBC => d đồng thời là đường trung trực
=> Tập hợp các điểm M thoả mãn đk đề bài là đường thẳng d là đường trung trực của BC
Cho tam giác ABC. Tập hợp các điểm M thỏa mãn
M
A
→
M
B
→
+
M
C
→
0
là: A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn.
Đọc tiếp
Cho tam giác ABC. Tập hợp các điểm M thỏa mãn M A → M B → + M C → = 0 là:
A. một điểm.
B. đường thẳng.
C. đoạn thẳng.
D. đường tròn.
Gọi I là trung điểm BC ⇒ M B → + M C → = 2 M I → .
Ta có M A → M B → + M C → = 0 ⇔ M A → .2 M I → = 0 ⇔ M A → . M I → = 0 ⇔ M A → ⊥ M I → . *
Biểu thức (*) chứng tỏ M A ⊥ M I hay M nhìn đoạn AI dưới một góc vuông nên tập hợp các điểm M là đường tròn đường kính AI.
Chọn D.
Đúng 0
Bình luận (0)
Cho tam giác ABC. Tập hợp các điểm M thỏa mãn
M
A
→
M
B
→
+
M
C
→
0
là A. Một điểm B. Một tia C. Một đường thẳng D. Một đường tròn
Đọc tiếp
Cho tam giác ABC. Tập hợp các điểm M thỏa mãn M A → M B → + M C → = 0 là
A. Một điểm
B. Một tia
C. Một đường thẳng
D. Một đường tròn
Cho tam giác ABC. Tìm tập hợp tất cả điểm M thỏa mãn điều kiện \(\overrightarrow{MA}+\overrightarrow{MB}-\overrightarrow{MC}=\overrightarrow{0}\)
\(\overrightarrow{MA}+\overrightarrow{MB}-\overrightarrow{MC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MA}-\overrightarrow{MC}=-\overrightarrow{MB}\Leftrightarrow\overrightarrow{CA}=\overrightarrow{BM}\)
Vậy M là điểm sao cho tứ giác ACBM là hình bình hành.
Đúng 0
Bình luận (0)
Cho ta giác ABC và điểm M thỏa mãn
M
A
→
M
B
→
-
M
C
→
Tập hợp điểm M là: A. Đường tròn tâm B, bán kính R AC B. Đường tròn tâm A, bán kính R BC C. Đường trung trực của...
Đọc tiếp
Cho ta giác ABC và điểm M thỏa mãn M A → = M B → - M C → Tập hợp điểm M là:
A. Đường tròn tâm B, bán kính R = AC
B. Đường tròn tâm A, bán kính R = BC
C. Đường trung trực của đoạn BC
D. Đường trung trực của đoạn AC
Câu 38. Cho tam giác ABC. Tìm tập hợp điểm M thỏa mãn 3|MA+MB| 2 |MA+ MB + MC| Câu 37. Trong mặt phẳng Oxy, cho tam giác ABC, có A(1;5), B(-2;2), C(3; - 1) . a. Tìm tọa độ điểm D sao cho ABCD là hình bình hành. b. Tìm tọa độ điểm E sao cho A là trung điểm đoạn BE. c. Tìm tọa độ điểm F sao cho B là trọng tâm tam giác ACF.
Đọc tiếp
Câu 38. Cho tam giác ABC. Tìm tập hợp điểm M thỏa mãn 3|MA+MB| =2 |MA+ MB + MC| Câu 37. Trong mặt phẳng Oxy, cho tam giác ABC, có A(1;5), B(-2;2), C(3; - 1) . a. Tìm tọa độ điểm D sao cho ABCD là hình bình hành. b. Tìm tọa độ điểm E sao cho A là trung điểm đoạn BE. c. Tìm tọa độ điểm F sao cho B là trọng tâm tam giác ACF.
38.
Gọi I là trung điểm AB và G là trọng tâm tam giác ABC
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}\\\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\end{matrix}\right.\)
\(3\left|\overrightarrow{MA}+\overrightarrow{MB}\right|=2\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|\)
\(\Leftrightarrow3.\left|2\overrightarrow{MI}\right|=3\left|\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\right|\)
\(\Leftrightarrow6\left|\overrightarrow{MI}\right|=2.\left|3\overrightarrow{MG}\right|\)
\(\Leftrightarrow6\left|\overrightarrow{MI}\right|=6\left|\overrightarrow{MG}\right|\)
\(\Leftrightarrow\left|\overrightarrow{MI}\right|=\left|\overrightarrow{MG}\right|\)
\(\Leftrightarrow MI=MG\)
\(\Rightarrow\) Tập hợp M là đường trung trực của đoạn thẳng IG
Đúng 1
Bình luận (0)
Cho tam giác ABC
a) Xác định điểm D thỏa mãn vecto DA +3. vecto DB=0
b) Tìm tập hợp điểm M thỏa mãn: |MA+MB|=|MA+MC| câu b đều là vecto hết nha mn















