Mn giải giúp e với

Những câu hỏi liên quan
mn giúp e với và giải thích giúp e ạ
B1
1. is
2. is
3. are
4. is
5. is/ am
6. aren't
7. are
8. Is she
9. is
10. are
B2
5. doesn't
7. don't
8. doesn't
9. don't
10. don't
B3
1. starts
2. likes
3. bake
4. writes
5. doesn't know
6. has
7. swim
8. helps
-----------
CT thì hiện tại đơn:
(+) S + V(s/es) + O
(-) S + don't/ doesn't + V + O
(?) Do/Does + S + V + O?
Tobe: am/is/are
- Nếu chủ ngữ là số ít, he, she, it thì tobe là is và V phải thêm s/es.
- Nếu chủ ngữ là số nhiều, you, we, they thì to be là are và V giữ nguyên.
- Nếu chủ ngữ là I thì tobe là am và V cũng giữ nguyên.
Đúng 8
Bình luận (0)
mn ơi giuos e với e đg cần gấp ạ và mn giải thích giúp e nx nha e cảm mơn
 mn ơi giúp em với ạ và giải thích giúp em e cảm ơn mn ❤
mn ơi giúp em với ạ và giải thích giúp em e cảm ơn mn ❤
Mn ơi giúp em giải với ạh,e cần gấp mong mn giúp em ạ.Em cảm ơn
mn giúp e giải với ạ 😭 e cảm ơn ạ
Mn giải giúp e bài này với ạ. E đang cần gấp
E đang cần gấp mn giải giúp e với đc k ạ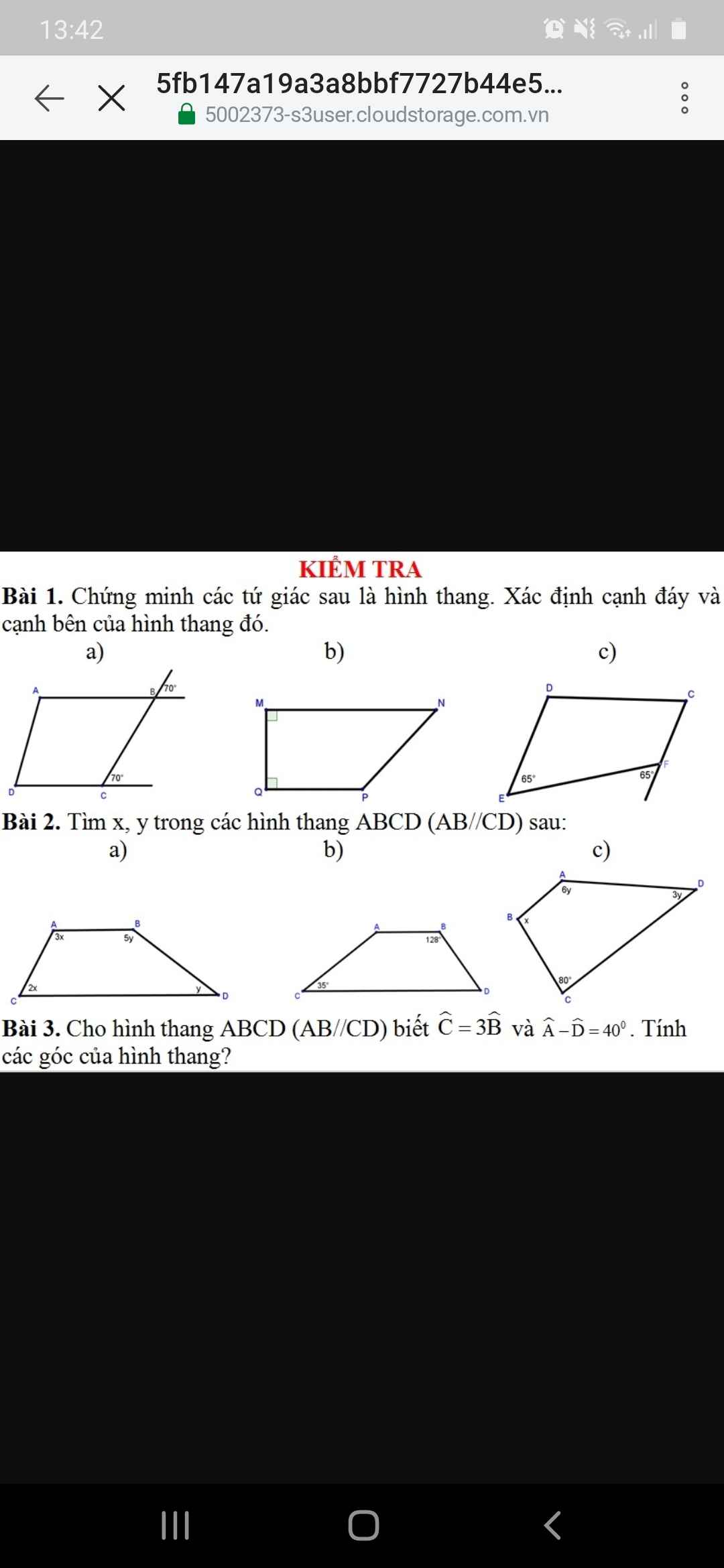
Bài 1
a) góc B=góc C=70 độ(gt)
=>AB//DC(đồng vị)
=> ABCD là hình thang
b)góc M+ góc Q=90 độ +90 độ=180 độ
=>MN//QP( hai góc trong cùng phía bù nhau)
=>MNPQ là hình thang
c)góc E= góc F=65 độ
=>DE//CF( slt)
=> DCFE là hình thang
Đúng 1
Bình luận (0)
Tham Khaor
Bài 1
a) góc B=góc C=70 độ(gt)
=>AB//DC(đồng vị)
=> ABCD là hình thang
b)góc M+ góc Q=90 độ +90 độ=180 độ
=>MN//QP( hai góc trong cùng phía bù nhau)
=>MNPQ là hình thang
c)góc E= góc F=65 độ
=>DE//CF( slt)
=> DCFE là hình thang
Đúng 1
Bình luận (0)
Bài 1:
a/ Góc B (ngoài) và góc C (ngoài) ở vị trí đồng vị, Góc B = Góc C ⇒ AB // CD
Vậy: ABCD là hình thang (đpcm), có cạnh đáy AB, CD và cạnh bên BC, AD
-----------
b/ MN ⊥ MQ, PQ ⊥ MQ ⇒ MN // PQ
Vậy: MNPQ là hình thang (đpcm), có cạnh đáy MN, PQ và cạnh bên NP, MQ
----------
c/ Góc DEF = Góc F (ngoài), hai góc ở vị trí so le trong ⇒ DE // CF
Vậy: CDEF là hình thang (đpcm), cạnh đáy DE, CF và cạnh bên CD, EF
==========
Bài 2:
a/ Ta có hai phương trình:
\(3x+2x=180\text{°}\) và \(y+5y=180\text{°}\) (do AB // CD)
Giải hai phương trình trên ta được: x=36° , y=30°
Vậy: \(\begin{matrix}\hat{A}=36\text{°}.3=108\text{°}\\\hat{B}=30\text{°}.5=150\text{°}\\\hat{C}=36\text{°}.2=72\text{°}\\\hat{D}=30\text{°}\end{matrix}\)
----------
b/ Do AB // CD, góc B = 128° và góc C = 35°
Vậy: \(\begin{matrix}\hat{A}=180\text{°}-35\text{°}=145\text{°}\\\hat{B}=128\text{°}\\\hat{C}=\hat{35\text{°}}\\\hat{D}=180\text{°}-128\text{°}=52\text{°}\end{matrix}\)
----------
c/ Do AB // CD
\(\Rightarrow x=180\text{°}-80\text{°}=100\text{°}\)
Ta có phương trình sau:
\(6y+3y=180\text{°}\)
Giải phương trình trên ta được y=20°
Vậy: \(\begin{matrix}\hat{A}=20\text{°}.6=120\text{°}\\\hat{B}=100\text{°}\\\hat{C}=80\text{°}\\\hat{D}=20\text{°}.3=60\text{°}\end{matrix}\)
==========
Bài 3:
- Do \(\hat{A}-\hat{D}=40\text{°}\Rightarrow\hat{A}=40\text{°}+\hat{D}\)
Ta có: \(\hat{A}+\hat{D}=180\text{°}\Leftrightarrow40\text{°}+2\hat{D}=180\text{°}\Leftrightarrow\hat{D}=70\text{°}\)
⇒ \(\hat{A}=110\text{°}\)
Mặt khác: \(\hat{A}+\hat{B}+\hat{C}+\hat{D}=360\text{°}\)
\(\Leftrightarrow110\text{°}+4\hat{B}+\hat{70\text{°}}=360\text{°}\)
\(\Leftrightarrow\hat{B}=45\text{°};\hat{C}=135\text{°}\)
Vậy: \(\begin{matrix}\hat{A}=110\text{°}\\\hat{B}=45\text{°}\\\hat{C}=135\text{°}\\\hat{D}=70\text{°}\end{matrix}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Mn giúp e giải bài này với
\(sinx-\sqrt{3}cos\left(x+\pi\right)=2sin2x\)
\(\Leftrightarrow sinx+\sqrt{3}cosx=2sin2x\)
\(\Leftrightarrow\dfrac{1}{2}sinx+\dfrac{\sqrt{3}}{2}cosx=sin2x\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{3}\right)=sin2x\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=x+\dfrac{\pi}{3}+k2\pi\\2x=\dfrac{2\pi}{3}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=\dfrac{2\pi}{9}+\dfrac{k2\pi}{3}\end{matrix}\right.\)
Cả 4 đáp án đều ko đúng
Đúng 1
Bình luận (0)
MN GIÚP E CÂU 5 VỚI Ạ. GIẢI CHI TIẾT CÁCH LÀM DÙM E VỚI Ạ.

Câu 5:
\(\Leftrightarrow-x^2+7x-9+2x-9=0\)
\(\Leftrightarrow x^2-9x+18=0\)
=>x=3
=>Chọn A
Đúng 5
Bình luận (0)



















