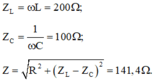Cho mạch điện \(RLC\) nối tiếp. Cuộn dây không thuần cảm có \(L = \frac{1,4}{\pi}H\) và \(r = 30\Omega\); tụ có \(C = 31,8\mu F\). \(R\) là biến trở. Điện áp hai đầu đoạn mạch có biểu thức: \(u = 100\sqrt2\cos(100\pi t)(V)\). Công suất của mạch cực đại khi điện trở có giá trị bằng:
A.\(15,5\Omega.\)
B.\(12\Omega.\)
C.\(10\Omega.\)
D.\(40\Omega.\)