help me zứi



help me zứi
Help me...Cíu tui zứi!

\(\dfrac{8\times3\times4}{16\times3}\)
\(=\dfrac{8\times3\times2\times2}{8\times2\times3}\)
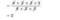
b) \(\dfrac{30\times25\times7\times8}{75\times8\times12\times14}\)

a)9x^3y^2+3x^2y^2 b)x^3+2x^2+3x c)6x^2y+4xy^2+2xy d)5x^2 (x-2y)-15x (x-2y) Help me zứi
Help zứi ạ! Cho mik xem phần hạ xuống nhoa! Mik tick cho

89744 | 28
84 | 3205
57
56
14
144
140
4
89744 | 28
84 | 3205
57
56
14
144
140
4
GIÚP MIK ZỨI Ạ ! CẢM ƠN !
Question 23: “Do you know Long’s address?” he asked me.
A. He asked me for Long’s address.
B. He asked me if someone knew Long’s address.
C. He asked me if I know Long’s address.
D. He asked me if I knew Long’s address.
Question 24: They are building a new bridge over the river.
A. A new bridge is building over the river.
B. A new bridge is being built over the river.
C. A new bridge is going to build over the river.
D. A new bridge is built over the river.
Question 25: I used to go to the cinema on Sundays.
A. I usually went to the cinema on Sundays.
B. I got used to going the cinema on Sundays.
C. I didn’t go to the cinema on Sundays.
D. I usually go to the cinema on Sundays.
Question 26: You feel unhealthy because you don’t take any exercise.
A. If you don’t take any exercise, you will feel healthy.
B. If you took more exercise, you would feel healthier.
C. If you take more exercise, you will feel healthier.
D. If you were healthier, you would take more exercise.
Mark the letter A, B, C, or D on your answer sheet to indicate the sentence that best combines each pair of sentences in the following questions.
Question 27: “Alice in the Wonderland” was written for children. It appeals to many adult readers.
A. Though for children written, “Alice in the Wonderland” appeals to many adult readers.
B. Though written for children, “Alice in the Wonderland” appeals to many adult readers.
C. Though it written for children, “Alice in the Wonderland” appeals to many adult readers.
D. Though writing for children, “Alice in the Wonderland” appeals to many adult readers.
Question 28: The agreement ended six-month negotiation. It was signed yesterday.
A. The agreement ended six-month negotiation which was signed yesterday.
B .The agreement which was signed yesterday lasted six months.
C. The negotiation which lasted six months was signed yesterday.
D. The agreement which was signed yesterday ended six-month negotiation.
Question 29: Think it through very carefully. Or else, you will not come up with the right answer.
A. If you think it through very carefully, you will not come up with the right answer.
B. Although you think it through very carefully, you will not come up with the right answer.
C. However carefully you think it through, you will not come up with the right answer.
D. Unless you think it through very carefully, you will not come up with the right answer.
Question 30: He felt very tired. However, he was determined to continue his work.
A. As the result of his tiredness, he was determined to continue his work.
B. He felt so tired that he was determined to continue his work.
C. Feeling tired, he was determined to continue his work.
D. Tired as he might feel, he was determined to continue his work
_____The end_____
Question 23: “Do you know Long’s address?” he asked me.
A. He asked me for Long’s address.
B. He asked me if someone knew Long’s address.
C. He asked me if I know Long’s address.
D. He asked me if I knew Long’s address.
Question 24: They are building a new bridge over the river.
A. A new bridge is building over the river.
B. A new bridge is being built over the river.
C. A new bridge is going to build over the river.
D. A new bridge is built over the river.
Question 25: I used to go to the cinema on Sundays.
A. I usually went to the cinema on Sundays.
B. I got used to going the cinema on Sundays.
C. I didn’t go to the cinema on Sundays.
D. I usually go to the cinema on Sundays.
Question 26: You feel unhealthy because you don’t take any exercise.
A. If you don’t take any exercise, you will feel healthy.
B. If you took more exercise, you would feel healthier.
C. If you take more exercise, you will feel healthier.
D. If you were healthier, you would take more exercise.
Mark the letter A, B, C, or D on your answer sheet to indicate the sentence that best combines each pair of sentences in the following questions.
Question 27: “Alice in the Wonderland” was written for children. It appeals to many adult readers.
A. Though for children written, “Alice in the Wonderland” appeals to many adult readers.
B. Though written for children, “Alice in the Wonderland” appeals to many adult readers.
C. Though it written for children, “Alice in the Wonderland” appeals to many adult readers.
D. Though writing for children, “Alice in the Wonderland” appeals to many adult readers.
Question 28: The agreement ended six-month negotiation. It was signed yesterday.
A. The agreement ended six-month negotiation which was signed yesterday.
B .The agreement which was signed yesterday lasted six months.
C. The negotiation which lasted six months was signed yesterday.
D. The agreement which was signed yesterday ended six-month negotiation.
Question 29: Think it through very carefully. Or else, you will not come up with the right answer.
A. If you think it through very carefully, you will not come up with the right answer.
B. Although you think it through very carefully, you will not come up with the right answer.
C. However carefully you think it through, you will not come up with the right answer.
D. Unless you think it through very carefully, you will not come up with the right answer.
Question 30: He felt very tired. However, he was determined to continue his work.
A. As the result of his tiredness, he was determined to continue his work.
B. He felt so tired that he was determined to continue his work.
C. Feeling tired, he was determined to continue his work.
D. Tired as he might feel, he was determined to continue his work
giúp me zứi : Tìm 1 phân số biết mẫu số hơn tử số 56 đơn vị và phân số có giá trị bằng 6/13
\(\frac{48}{104}\)
giúp zứi

 cíu zứi
cíu zứi
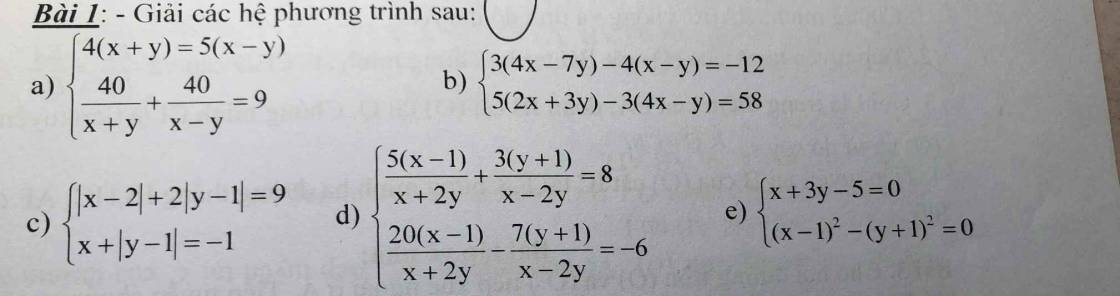 cíu zứi
cíu zứi
a:
ĐKXĐ: \(x\ne\pm y\)
4(x+y)=5(x-y)
=>\(\dfrac{x+y}{5}=\dfrac{x-y}{4}=k\)
=>\(x+y=5k;x-y=4k\)
\(\dfrac{40}{x+y}+\dfrac{40}{x-y}=9\)
=>\(\dfrac{40}{5k}+\dfrac{40}{4k}=9\)
=>\(\dfrac{8}{k}+\dfrac{10}{k}=9\)
=>18/k=9
=>k=2
=>\(x+y=10;x-y=8\)
=>\(\left\{{}\begin{matrix}x+y+x-y=10+8=18\\x-y=8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=18\\x-y=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=9\\y=x-8=1\end{matrix}\right.\)(nhận)
b: \(\left\{{}\begin{matrix}3\left(4x-7y\right)-4\left(x-y\right)=-12\\5\left(2x+3y\right)-3\left(4x-y\right)=58\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}12x-21y-4x+4y=-12\\10x+15y-12x+3y=58\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}8x-17y=-12\\-2x+18y=58\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}8x-17y=-12\\-8x+72y=232\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}55y=220\\8x-17y=-12\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=4\\8x=-12+17y=-12+17\cdot4=56\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=7\\y=4\end{matrix}\right.\)
d:
ĐKXĐ: \(x\ne\pm2y\)
\(\left\{{}\begin{matrix}\dfrac{5\left(x-1\right)}{x+2y}+\dfrac{3\left(y+1\right)}{x-2y}=8\\\dfrac{20\left(x-1\right)}{x+2y}-7\cdot\dfrac{\left(y+1\right)}{x-2y}=-6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{20\left(x-1\right)}{x+2y}+\dfrac{12\left(y+1\right)}{x-2y}=32\\\dfrac{20\left(x-1\right)}{x+2y}-\dfrac{7\left(y+1\right)}{x-2y}=-6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{19\left(y+1\right)}{x-2y}=38\\\dfrac{20\left(x-1\right)}{x+2y}-\dfrac{7\left(y+1\right)}{x-2y}=-6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{y+1}{x-2y}=2\\\dfrac{20\left(x-1\right)}{x+2y}=-6+7\cdot2=8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-4y=y+1\\20\left(x-1\right)=8\left(x+2y\right)\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-5y=1\\20x-20=8x+16y\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-5y=1\\12x-16y=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}12x-30y=6\\12x-16y=20\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-14y=-14\\2x-5y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1\\2x=5y+1=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\)(nhận)
e: \(\left\{{}\begin{matrix}x+3y-5=0\\\left(x-1\right)^2-\left(y+1\right)^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-3y+5\\\left(-3y+5-1\right)^2-\left(y+1\right)^2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-3y+5\\\left(-3y+4\right)^2-\left(y+1\right)^2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-3y+5\\\left(3y-4\right)^2-\left(y+1\right)^2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-3y+5\\\left(3y-4-y-1\right)\left(3y-4+y+1\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-3y+5\\\left(2y-5\right)\left(4y-3\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3y+5\\\left[{}\begin{matrix}2y-5=0\\4y-3=0\end{matrix}\right.\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\left\{{}\begin{matrix}y=\dfrac{5}{2}\\x=-3y+5=-3\cdot\dfrac{5}{2}+5=-\dfrac{15}{2}+5=-\dfrac{5}{2}\end{matrix}\right.\\\left\{{}\begin{matrix}y=\dfrac{3}{4}\\x=-3y+5=-3\cdot\dfrac{3}{4}+5=-\dfrac{9}{4}+5=\dfrac{11}{4}\end{matrix}\right.\end{matrix}\right.\)
c: TH1: x>=2
Hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}x-2+2\left|y-1\right|=9\\x+\left|y-1\right|=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+2\left|y-1\right|=11\\x+\left|y-1\right|=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left|y-1\right|=12\\x+\left|y-1\right|=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-1-12=-13\left(loại\right)\\\left|y-1\right|=12\end{matrix}\right.\)
=>Loại
TH2: x<2
Hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}-x+2+2\left|y-1\right|=9\\x+\left|y-1\right|=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-x+2\left|y-1\right|=7\\x+\left|y-1\right|=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3\left|y-1\right|=6\\x+\left|y-1\right|=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left|y-1\right|=2\\x=-1-2=-3\left(nhận\right)\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-3\\\left[{}\begin{matrix}y-1=2\\y-1=-2\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\\left[{}\begin{matrix}y=3\\y=-1\end{matrix}\right.\end{matrix}\right.\)