a:
ĐKXĐ: \(x\ne\pm y\)
4(x+y)=5(x-y)
=>\(\dfrac{x+y}{5}=\dfrac{x-y}{4}=k\)
=>\(x+y=5k;x-y=4k\)
\(\dfrac{40}{x+y}+\dfrac{40}{x-y}=9\)
=>\(\dfrac{40}{5k}+\dfrac{40}{4k}=9\)
=>\(\dfrac{8}{k}+\dfrac{10}{k}=9\)
=>18/k=9
=>k=2
=>\(x+y=10;x-y=8\)
=>\(\left\{{}\begin{matrix}x+y+x-y=10+8=18\\x-y=8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=18\\x-y=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=9\\y=x-8=1\end{matrix}\right.\)(nhận)
b: \(\left\{{}\begin{matrix}3\left(4x-7y\right)-4\left(x-y\right)=-12\\5\left(2x+3y\right)-3\left(4x-y\right)=58\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}12x-21y-4x+4y=-12\\10x+15y-12x+3y=58\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}8x-17y=-12\\-2x+18y=58\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}8x-17y=-12\\-8x+72y=232\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}55y=220\\8x-17y=-12\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=4\\8x=-12+17y=-12+17\cdot4=56\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=7\\y=4\end{matrix}\right.\)
d:
ĐKXĐ: \(x\ne\pm2y\)
\(\left\{{}\begin{matrix}\dfrac{5\left(x-1\right)}{x+2y}+\dfrac{3\left(y+1\right)}{x-2y}=8\\\dfrac{20\left(x-1\right)}{x+2y}-7\cdot\dfrac{\left(y+1\right)}{x-2y}=-6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{20\left(x-1\right)}{x+2y}+\dfrac{12\left(y+1\right)}{x-2y}=32\\\dfrac{20\left(x-1\right)}{x+2y}-\dfrac{7\left(y+1\right)}{x-2y}=-6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{19\left(y+1\right)}{x-2y}=38\\\dfrac{20\left(x-1\right)}{x+2y}-\dfrac{7\left(y+1\right)}{x-2y}=-6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{y+1}{x-2y}=2\\\dfrac{20\left(x-1\right)}{x+2y}=-6+7\cdot2=8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-4y=y+1\\20\left(x-1\right)=8\left(x+2y\right)\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-5y=1\\20x-20=8x+16y\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-5y=1\\12x-16y=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}12x-30y=6\\12x-16y=20\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-14y=-14\\2x-5y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1\\2x=5y+1=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\)(nhận)
e: \(\left\{{}\begin{matrix}x+3y-5=0\\\left(x-1\right)^2-\left(y+1\right)^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-3y+5\\\left(-3y+5-1\right)^2-\left(y+1\right)^2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-3y+5\\\left(-3y+4\right)^2-\left(y+1\right)^2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-3y+5\\\left(3y-4\right)^2-\left(y+1\right)^2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-3y+5\\\left(3y-4-y-1\right)\left(3y-4+y+1\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-3y+5\\\left(2y-5\right)\left(4y-3\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3y+5\\\left[{}\begin{matrix}2y-5=0\\4y-3=0\end{matrix}\right.\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\left\{{}\begin{matrix}y=\dfrac{5}{2}\\x=-3y+5=-3\cdot\dfrac{5}{2}+5=-\dfrac{15}{2}+5=-\dfrac{5}{2}\end{matrix}\right.\\\left\{{}\begin{matrix}y=\dfrac{3}{4}\\x=-3y+5=-3\cdot\dfrac{3}{4}+5=-\dfrac{9}{4}+5=\dfrac{11}{4}\end{matrix}\right.\end{matrix}\right.\)
c: TH1: x>=2
Hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}x-2+2\left|y-1\right|=9\\x+\left|y-1\right|=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+2\left|y-1\right|=11\\x+\left|y-1\right|=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left|y-1\right|=12\\x+\left|y-1\right|=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-1-12=-13\left(loại\right)\\\left|y-1\right|=12\end{matrix}\right.\)
=>Loại
TH2: x<2
Hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}-x+2+2\left|y-1\right|=9\\x+\left|y-1\right|=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-x+2\left|y-1\right|=7\\x+\left|y-1\right|=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3\left|y-1\right|=6\\x+\left|y-1\right|=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left|y-1\right|=2\\x=-1-2=-3\left(nhận\right)\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-3\\\left[{}\begin{matrix}y-1=2\\y-1=-2\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\\left[{}\begin{matrix}y=3\\y=-1\end{matrix}\right.\end{matrix}\right.\)

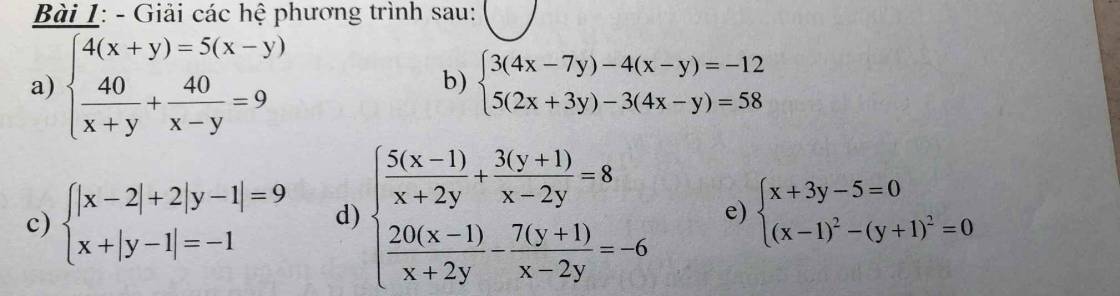 cíu zứi
cíu zứi


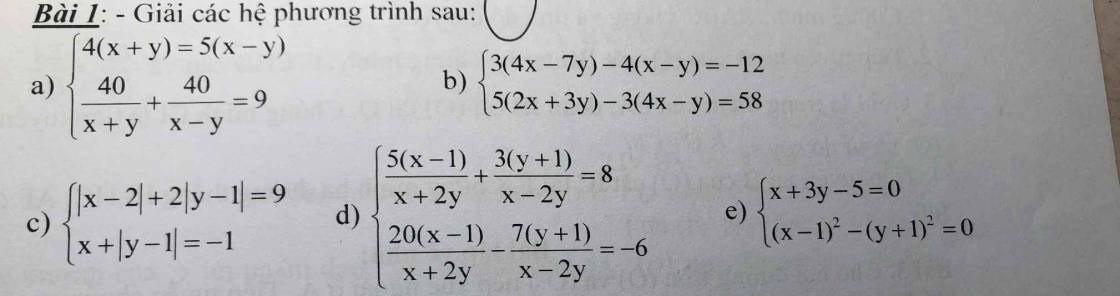 cíu zứi
cíu zứi cíu cíu
cíu cíu

 cíu tui cíu tui
cíu tui cíu tui cíu tui cíu tui
cíu tui cíu tui
 cíu lẹ cíu lẹ
cíu lẹ cíu lẹ 
 cíu tui cíu tui
cíu tui cíu tui