
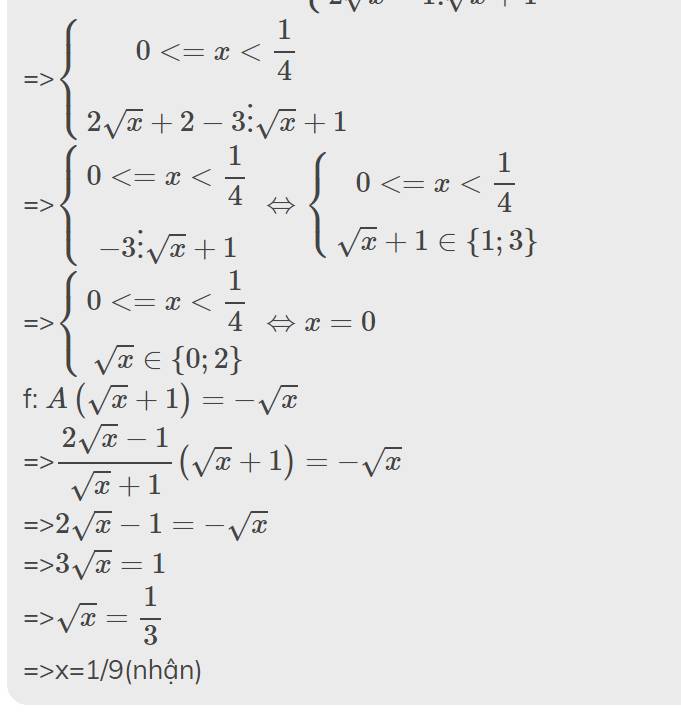
g: A<1
=>\(\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}< 1\)
=>\(\dfrac{2\sqrt{x}-1-\sqrt{x}-1}{\sqrt{x}+1}< 0\)
=>\(\sqrt{x}-2< 0\)
=>\(\sqrt{x}< 2\)
=>0<=x<4
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}0< =x< 4\\x< >1\end{matrix}\right.\)
h: \(A=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\)
=>\(A=\dfrac{2\sqrt{x}+2-3}{\sqrt{x}+1}=2-\dfrac{3}{\sqrt{x}+1}\)
\(\sqrt{x}+1>=1\forall x\) thỏa mãn ĐKXĐ
=>\(\dfrac{3}{\sqrt{x}+1}< =\dfrac{3}{1}=3\forall x\) thỏa mãn ĐKXĐ
=>\(-\dfrac{3}{\sqrt{x}+1}>=-3\forall x\) thỏa mãn ĐKXĐ
=>\(-\dfrac{3}{\sqrt{x}+1}+2>=-3+2=-1\forall x\) thỏa mãn ĐKXĐ
=>\(A>=-1\forall x\) thỏa mãn ĐKXĐ
Vậy: \(A_{min}=-1\) khi x=0
i: \(P=A\left(-x+2\sqrt{x}+3\right)\)
\(=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\cdot\left(-1\right)\cdot\left(x-2\sqrt{x}-3\right)\)
\(=\dfrac{1-2\sqrt{x}}{\sqrt{x}+1}\cdot\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)\)
\(=\left(1-2\sqrt{x}\right)\left(\sqrt{x}-3\right)\)
\(=\sqrt{x}-3-2x+6\sqrt{x}=-2x+7\sqrt{x}-3\)
\(=-2\left(x-\dfrac{7}{2}\sqrt{x}+\dfrac{3}{2}\right)\)
\(=-2\left(x-2\cdot\sqrt{x}\cdot\dfrac{7}{4}+\dfrac{49}{16}-\dfrac{1}{16}\right)\)
\(=-2\left(\sqrt{x}-\dfrac{7}{4}\right)^2+\dfrac{1}{8}< =\dfrac{1}{8}\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi \(\sqrt{x}-\dfrac{7}{4}=0\)
=>\(\sqrt{x}=\dfrac{7}{4}\)
=>\(x=\dfrac{49}{16}\)

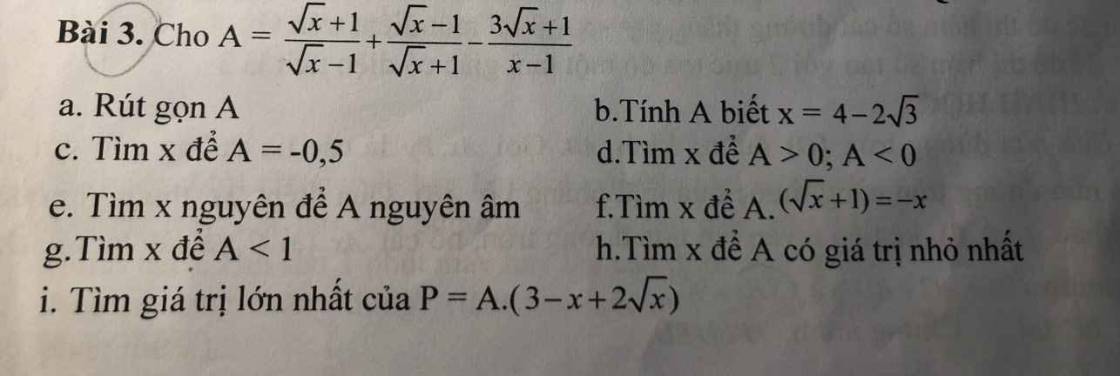 cíu cíu
cíu cíu


 cíu tui cíu tui
cíu tui cíu tui cíu tui cíu tui
cíu tui cíu tui cíu tui cíu tui
cíu tui cíu tui cíu lẹ cíu lẹ
cíu lẹ cíu lẹ