tìm giá trị biểu thức \(J=C_{20}^0-2^2C^1_{20}+2^4C^2_{20}-...+2^{40}C^{20}_{20}\)

Những câu hỏi liên quan
Tính tổng: \(S=C^1_{20}+2C^2_{20}+2^2C^3_{20}+...+2^{19}C^{20}_{20}\)
Xét khai triển:
\(\left(x+1\right)^{20}=C_{20}^0+C_{20}^1x+C_{20}^2x^2+...+C_{20}^{20}x^{20}\)
Chia 2 vế cho x ta được:
\(\dfrac{\left(x+1\right)^{20}}{x}=\dfrac{1}{x}+C_{20}^1+C_{20}^2x+...+C_{20}^{20}.x^{19}\)
Thay \(x=2\)
\(\Rightarrow\dfrac{3^{20}}{2}=\dfrac{1}{2}+C_{20}^1+2C_{20}^2+2^2C_{20}^3+...+2^{19}C_{20}^{20}\)
\(\Rightarrow S=\dfrac{3^{20}-1}{2}\)
Đúng 2
Bình luận (0)
`S=C_20 ^1 + 2C_20 ^2 + 2^2 C_20 ^3 +....+2^19 C_20 ^20`
`<=>2S=2C_20 ^1+2^2 C_20 ^2 + 2^3 C_20 + .... + 2^20 C_20 ^20`
`<=>2S=C_20 ^0 +2C_20 ^1+2^2 C_20 ^2 + 2^3 C_20 + .... + 2^20 C_20 ^20 -C_20 ^0`
`<=>2S=(1+2)^20-1`
`<=>2S=3^20-1`
`<=>S=[3^20 -1]/2`
Đúng 1
Bình luận (0)
Sử dụng máy tính cầm tay, tính giá trị các biểu thức sau:
a) \(A_{15}^{10}\)
b) \(C_{10}^6 + C_{10}^7 + C_{11}^8\)
c) \(C_5^1C_{20}^2 + C_5^2C_{20}^1\)
a) Để tính \(A_{15}^{10}\) ta ấn liên tiếp các phím
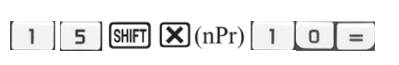
Thì nhận được kết quả là \(1,{08972864.10^{10}}\)
b) Để tính \(C_{10}^6 + C_{10}^7 + C_{11}^8\) thì ta ấn liên tiếp các phím

Thì ta nhận được kết quả là 495
c) Để tính \(C_5^1C_{20}^2 + C_5^2C_{20}^1\) thì ta ấn liên tiếp các phím

Thì ta được kết quả là 1150
Đúng 0
Bình luận (0)
1. Tìm giá trị lớn nhất của biểu thức T, biết T = (x-13)2 - 26
2. Tìm giá trị lớn nhất của biểu thức M, biết M = 20 - (x-14)2
3. Tìm m và n biết (20 - m - n)2 + (m - 13)2 <= 0
4. Tìm y biết: (20 + y)2 -144 = 0
5. Tìm Z biết: (Z - 15)2 + 37 = 0
1.
Ta thấy $(x-13)^2\geq 0$ với mọi $x$
$\Rightarrow T=(x-13)^2-26\geq 0-26=-26$
Vậy GTNN của $T$ là $-26$.
Giá trị này đạt tại $x-13=0\Leftrightarrow x=13$
Đúng 0
Bình luận (0)
2.
Ta thấy: $(x-14)^2\geq 0$ với mọi $x$
$\Rightarrow M=20-(x-14)^2\leq 20-0=20$
Vậy $M_{\max}=20$. Giá trị này đạt tại $x-14=0$
Hay $x=14$.
Đúng 0
Bình luận (0)
3.
Ta thấy: $(20-m-n)^2\geq 0$ với mọi $m,n$
$(m-13)^2\geq 0$ với mọi $m$
$\Rightarrow (20-m-n)^2+(m-13)^2\geq 0$ với mọi $m,n$
Do đó để $(20-m-n)^2+(m-13)^2\leq 0$ thì:
$(20-m-n)^2+(m-13)^2=0$
Điều này xảy ra khi $(20-m-n)^2=(m-13)^2=0$
$\Leftrightarrow m=13; m+n=20\Leftrightarrow m=13; n=7$
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
bài 4; tính giá trị biểu thức
a, C = x mũ 2 - z mũ 2 + 4y mũ 2 + 4xy tại x = 40, y= 20, z = 20
b, D = x mũ 2 + 4xy + 4y mũ 2 - z mũ 2 + 2zt - t mũ 2 tại X = 10, Y= 40, Z = 30, T = 20
c, A =
12, tìm hệ số x26trong khai triển : \(\left(1+x^7\right)^n\), x khác 0 biết :
\(C^1_{2n+1}+C^2_{2n+1}+...+C^n_{2n+1}=2^{20}-1\)
Tìm giá trị biểu thức \(C=2x^6y-3xy^3-20\) với x,y thỏa mãn \(\left|x+1\right|+\left(y-2\right)^2=0\)
-Có \(\left|x+1\right|+\left(y-2\right)^2=0\)
-Vì \(\left|x+1\right|\ge0\forall x;\left(y-2\right)^2\ge0\forall y\)
\(\Rightarrow\left|x+1\right|=0\) ; \(\left(y-2\right)^2=0\)
\(\Rightarrow x=-1;y=2\)
-Thay \(x=-1;y=2\) vào \(C=2x^6y-3xy^3-20\) ta được:
\(C=2.\left(-1\right)^6.2-3.\left(-1\right).2^3-20=8\)
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức
\(C=x^2-8x+20\)
\(C=x^2-8x+20\\ C=x^2-8x+16+4\\ C=\left(x-4\right)^2+4\ge4\)
\(MinC=0\Leftrightarrow x-4=0\Leftrightarrow x=4\\ MinC=4\Leftrightarrow x=4\)
Đúng 1
Bình luận (0)
Giá trị nhỏ nhất của biểu thức là
Ta có : R = \(9x^2\) - \(6xy+2y^2\) + \(5\)
= \(\left(3x\right)^2\) - \(2.3x.\sqrt{2}^2\) + \(\left(\sqrt{2}y\right)^2\) + 5
= \(\left(3x-\sqrt{2}y\right)^2\) + 5
Vậy min R = 5 khi \(\left(3x-\sqrt{2}y\right)^2\) =0
Đúng 0
Bình luận (0)
Tìm giá trị của biến số để mỗi biểu thức sau có giá trị bằng 0:
a) \(5y^2-20\)
b) \(\left|y-1\right|+5\)






















