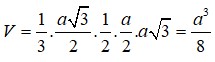Chóp SABC có (SAB)⏊(ABC), △SAB và △ABC đều cạnh a. Tính d(SC,AB)

Những câu hỏi liên quan
cho hình chóp sabc có sa=sb=sc=2a, tam giác abc đều cạnh a. tính thể tích khối chóp sab
Gọi H là tâm đáy \(\Rightarrow SH\perp\left(ABC\right)\)
Ta có: \(AH=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\)
Áp dụng định lý Pitago:
\(SH=\sqrt{SA^2-AH^2}=\dfrac{a\sqrt{33}}{3}\)
\(V=\dfrac{1}{3}SH.S_{ABC}=\dfrac{1}{3}.\dfrac{a\sqrt{33}}{3}.\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^3\sqrt{11}}{12}\)
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có mp(SAB)
⊥
mp(ABC), tam giác ABC đều cạnh 2a, tam giác SAB vuông cân tại S. Tính thể tích hình chóp SABC A.
a
3
3
3
B.
a
3
3...
Đọc tiếp
Cho hình chóp S.ABC có mp(SAB) ⊥ mp(ABC), tam giác ABC đều cạnh 2a, tam giác SAB vuông cân tại S. Tính thể tích hình chóp SABC
A. a 3 3 3
B. a 3 3 6
C. 2 a 3 3 3
D. a 3 3 12
Đáp án là A
![]()
![]()
![]()
Ta có :
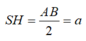
( Do SAB là tam giác vuông cân tại S cạnh huyền AB=2a)
Diện tích tam giác ABC là

Vậy thể tích khối chóp SABC là:
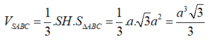
Đúng 0
Bình luận (0)
cho hình chóp SABC có đáy là tam giác đều cạnh 4a. M là trung điểm cạnh BC, H là trung điểm cạnh AM, SH vuông góc với (ABC), góc giữa ((SAB),(ABC)) = 60 độ. Tính V SABC và ((SAB),(SAC))
Cho hình chóp SABC có mặt phẳng (SAC) vuông góc với mặt phẳng (ABC), SAB là tam giác đều cạnh
a
3
,
B
C
a
3
, đường thẳng SC tạo với mặt phẳng (ABC) góc
60
0
. Thể tích của khối chóp SABC bằng:
Đọc tiếp
Cho hình chóp SABC có mặt phẳng (SAC) vuông góc với mặt phẳng (ABC), SAB là tam giác đều cạnh a 3 , B C = a 3 , đường thẳng SC tạo với mặt phẳng (ABC) góc 60 0 . Thể tích của khối chóp SABC bằng:
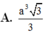
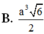
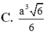
![]()
Cho hình chóp SABC có mặt phẳng (SAC) vuông góc với mặt phẳng (ABC) , SABlà tam giác đều cạnh
a
3
,
B
C
a
3
,
đường thẳng SC tạo với mặt phẳng (ABC) góc
60
0
. Thể tích của khối chóp SABC bằng: A.
a
3
3
3...
Đọc tiếp
Cho hình chóp SABC có mặt phẳng (SAC) vuông góc với mặt phẳng (ABC) , SAB
là tam giác đều cạnh a 3 , B C = a 3 , đường thẳng SC tạo với mặt phẳng (ABC) góc 60 0 . Thể tích của khối chóp SABC bằng:
A. a 3 3 3
B. a 3 6 2
C. a 3 6 6
D. 2 a 3 6
Cho hình chóp SABC có đáy ABC là tam giác vuôg tại B và có SA vuôg vs mp (ABC). a/ cm: BC vuôg (SAB) b/ Giả sử SA=a căn 3 và AB= a, tính góc giữa đường thẳng SB và mp(ABC) c/ Gọi AM là đường cao của tam giác SAB, N là điểm thuộc cạnh SC. cm: (AMN) vuôg (SBC)?
Cho hình chóp S.ABC có đáy ABC đều cạnh a, SA
⊥
(ABC)., SA
a
2
2
. Tính góc giữa SC và mặt phẳng (SAB) A. 450 B. 600 C. 900 D. 300
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC đều cạnh a, SA ⊥ (ABC)., SA = a 2 2 . Tính góc giữa SC và mặt phẳng (SAB)
A. 450
B. 600
C. 900
D. 300
Đáp án A
Phương pháp:
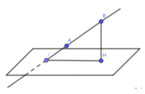
- Xác định góc giữa đường thẳng AB và mặt phẳng (P):
Bước 1: Xác định giao điểm I của AB và (P)
Bước 2: Từ B hạ BH vuông góc với (P)
Bước 3: Nối IH => Góc HIB là góc tạo bởi AB và (P).
Cách giải:
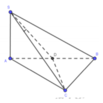
Gọi D là trung điểm của AB.
Tam giác ABC đều => CD ⊥ AB
Mà CD ⊥ SA, do SA ⊥ (ABC)
=> CD ⊥ (SAB) => (SC, (SAB)) = (SC, SD) = CSD
Tam giác ABC đều, cạnh a, M là trung điểm AB
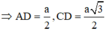
Tam giác ADS vuông tại A
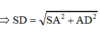
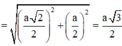
Tam giác SDC vuông tại D
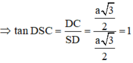
![]()
Đúng 0
Bình luận (0)
Cho hình chóp SABC có ABa,
A
B
a
3
,
A
B
C
^
30
°
. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối chóp SABC. A.
V
a
3
8
B.
V
a...
Đọc tiếp
Cho hình chóp SABC có AB=a, A B = a 3 , A B C ^ = 30 ° . Tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối chóp SABC.
A. V = a 3 8
B. V = a 3 2
C. V = a 3 3 7
D. V = a 3 3 17
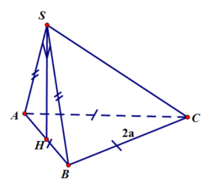
Hình chóp SABC có ∆ SAB, ∆ SBC là các tam giác đều cạnh a, mp(SAC) ⊥ mp(ABC). Tính AC.
A. AC = 2a.
B. AC = a 3 .
C. AC = a 2 .
D. AC = a.