Question

Chóp SABC có (SAB)⏊(ABC), △SAB và △ABC đều cạnh a. Tính d(SC,AB)

Answer 1

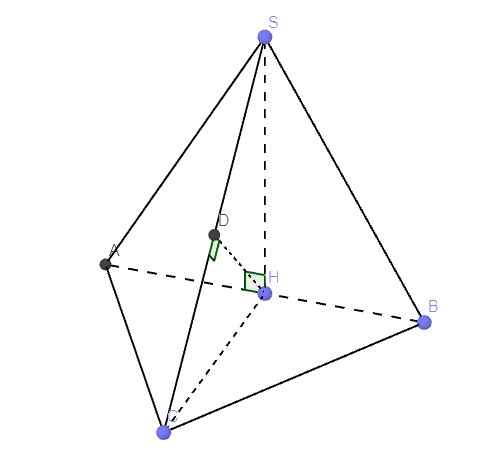
Gọi H là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}SH\perp AB\\CH\perp AB\end{matrix}\right.\) do các tam giác SAB và ABC đều

\(\Rightarrow AB\perp\left(SCH\right)\)

Trong mp (SCH), từ H kẻ \(HD\perp SC\)

\(\Rightarrow HD\) là đường vuông góc chung của AB và SC

\(\Rightarrow HD=d\left(SC,AB\right)\)

\(SH=CH=\dfrac{a\sqrt{3}}{2}\Rightarrow\Delta SCH\) vuông cân tại H

\(\Rightarrow HD=\dfrac{1}{2}SC=\dfrac{1}{2}.SH.\sqrt{2}=\dfrac{a\sqrt{6}}{4}\)

Answer 2