Những câu hỏi liên quan
cho tam giác abc có 3 góc nhọn. Vẽ đường cáo AD, BE, CF cắt nhau tại H. Chứng minh:
a) \(0< cos^2A+cos^2B+cos^2C< 1\)
b)\(2< sin^2A+sin^2B+sin^2C< 3\)
c)sinA + sinB + sinC < 2( cosA + cosB + cosC)
d)sinB . cosC + sinC . cosB = sinA
e)tanA + tanB + tanC = tanA . tanB . tanC
cho tam giác abc sao cho AB=c AC=b BC=a
a) a/sinA=b/sinB=c/sinC
b) cm căn(a*sinA)+ căn(b*sinB)+ căn(c*sinC)=căn[(a+b+c)(sinA+sinB+sinC)]
SinA+SinB+SinC > 2.Với A,B,C là ba góc nhọn trong tam giác.
CosA+CosB+CosC <= 2/3.Với A,B,C là ba góc nhọn trong tam giác.
CotA+CotB+CotC <= căn bậc hai của 3.Với A,B,C là ba góc nhọn trong tam giác.
Cho tam giác ABC vuông tại A a) chứng minh tanB + cosB lớn hơn bằng 2 b) Khi sinB + cosB=căn 2 . Hãy tính góc B c) H là trung điểm AB, đường thẳng qua H vuông góc với BC tại I và cắt tia AC tại K. Chứng minh tan C x tan BKC =2
Cho tam giác ABC vuông tại A
a) chứng minh tanB + cosB lớn hơn bằng 2
b) Khi sinB + cosB=căn 2 . Hãy tính góc B
c) H là trung điểm AB, đường thẳng qua H vuông góc với BC tại I và cắt tia AC tại K. Chứng minh tan C x tan BKC =2
Đúng 0
Bình luận (0)
Chóp SABCD , ABCD là hình chữ nhật tâm O SA=5a ; AB=2a ; AD=a căn 3 ; SA vuông góc với đáy a) Cm BC vuông góc (SAB) ; CD vuông góc (SAD ) ; (SCD) vuông góc (SAD) b) Tính góc (SC:SAD) ; (SC:SAD) ; (SC:ABCD) c) Tính khoảng cách từ A đến (SBC) và d(A,(SCD)) d)Tính góc giữa 2 mp (SBD) và (ABCD) ; (SCD) và (ABCD)
a: BC vuông góc SA
BC vuông góc AB
=>CB vuông góc (SBA)
DC vuông góc AD
DC vuông góc SA
=>DC vuông góc (SAD)
=>(SDC) vuông góc (SAD)
b: (SC;(SAD))=(SC;SD)=góc CSD
\(SD=\sqrt{SA^2+AD^2}=2a\sqrt{7}\)
\(AC=\sqrt{\left(2a\right)^2+3a^2}=a\sqrt{7}\)
\(SC=\sqrt{SA^2+AC^2}=4a\sqrt{2}\)
\(cosCSD=\dfrac{SC^2+SD^2-DC^2}{2\cdot SC\cdot SD}=\dfrac{32a^2+28a^2-4a^2}{2\cdot2a\sqrt{7}\cdot4a\sqrt{2}}=\dfrac{\sqrt{14}}{4}\)
=>góc CSD=21 độ
(SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=5/căn 7
=>góc SCA=62 độ
Đúng 1
Bình luận (0)
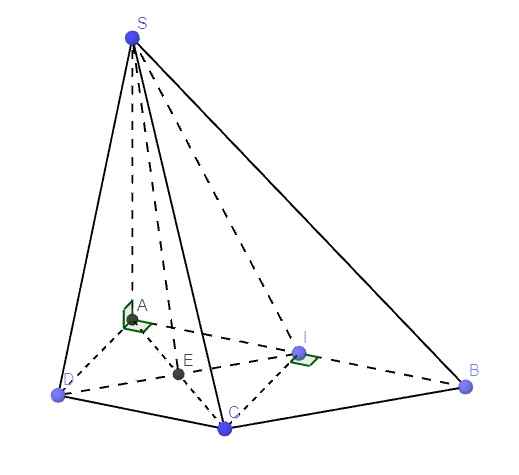
Cho hình chóp S.ABCD, đáy ABCD là hình thang vuông tại A và D. SA=a căn (3), AB=2a, AD=DC=a. Gọi I là trung điểm AB. SA vuông góc với (ABCD) a. Tính góc giữa mp (SDC) và mp (ABCD) b. Tính góc giữa mp (SDI) và mp (ABCD) c. CM (SCI) vuông góc với (SAB) d. CM (SBC) vuông góc với (SAC)
c.
Từ câu b ta có AICD là hình vuông \(\Rightarrow CI\perp AB\)
Mà \(SA\perp\left(ABCD\right)\Rightarrow SA\perp CI\)
\(\Rightarrow CI\perp\left(SAB\right)\)
Lại có \(CI\in\left(SCI\right)\Rightarrow\left(SCI\right)\perp\left(SAB\right)\)
d.
I là trung điểm AB \(\Rightarrow CI\) là trung tuyến ứng với AB
Lại có \(CI=AD=a\) (AICD là hình vuông) \(\Rightarrow CI=\dfrac{1}{2}AB\)
\(\Rightarrow\Delta ACB\) vuông tại C
\(\Rightarrow BC\perp AC\) (1)
Mà \(SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\) (2)
(1);(2) \(\Rightarrow BC\perp\left(SAC\right)\)
\(BC\in\left(SBC\right)\Rightarrow\left(SBC\right)\perp\left(SAC\right)\)
Đúng 2
Bình luận (0)
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
Mà \(CD=\left(SCD\right)\cap\left(ABCD\right)\)
\(\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và (ABCD)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\sqrt{3}\Rightarrow\widehat{SDA}=60^0\)
b.
Gọi E là giao điểm AC và DI
I là trung điểm AB \(\Rightarrow AI=\dfrac{1}{2}AB=a\Rightarrow AI=DC\)
\(\Rightarrow AICD\) là hình bình hành
Mà \(\widehat{A}=90^0\Rightarrow AICD\) là hình chữ nhật
\(AI=AD=a\) (hai cạnh kề bằng nhau) \(\Rightarrow AICD\) là hình vuông
\(\Rightarrow AC\perp DI\) tại E
Lại có \(SA\perp\left(ABCD\right)\Rightarrow SA\perp DI\Rightarrow DI\perp\left(SAE\right)\)
Mà \(DI=\left(SDI\right)\cap\left(ABCD\right)\Rightarrow\widehat{SEA}\) là góc giữa (SDI) và (ABCD)
\(AE=\dfrac{1}{2}AC=\dfrac{1}{2}\sqrt{AD^2+CD^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow tan\widehat{SEA}=\dfrac{SA}{AE}=\dfrac{\sqrt{6}}{2}\Rightarrow\widehat{SEA}\approx50^046'\)
Đúng 2
Bình luận (1)
Xem thêm câu trả lời
Cho hình chóp SABC có đáy là tam giác ABC vuông tại B, AB= 3a, BC= 4a (SBC) vuông ( ABC), SB= 2a căn 3, góc SBC= 30.
a. Tính V(SABC)
b. Tính d(B;(SAC))
1. Cho tam giác ABC, góc A=90 độ. BC=10cm. sinB=\(\frac{3}{4}\)
Tính AB, AC, góc B, góc C
Ta có: \(AC=BC\cdot\sin B=10\cdot\frac{3}{4}=7,5\left(cm\right)\)
\(\Rightarrow AB=\sqrt{BC^2-CA^2}=\sqrt{100-\frac{225}{4}}=\frac{5\sqrt{7}}{2}\left(cm\right)\)
Từ đó ta tính được:
\(\widehat{B}=49^0\) ; \(\sin C=\frac{AB}{BC}=\frac{\sqrt{7}}{4}\) \(\Rightarrow\widehat{C}=41^0\)
Vậy \(\hept{\begin{cases}AB=\frac{5\sqrt{7}}{2}\left(cm\right)\\AC=7,5\left(cm\right)\end{cases}}\) và \(\hept{\begin{cases}\widehat{B}=49^0\\\widehat{C}=41^0\end{cases}}\) (số đo góc chỉ xấp xỉ)
cho tam giác ABC, góc A =90 độ, AB=12cm
CosB=\(\frac{3}{5}\). Tính AC, BC, góc B, góc C
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AC=a căn 3, BC = 2a, SA vuông góc (ABCD), SA=3a. Gọi O là giao điểm của AC và BD. a) Cmr: CD vuông góc mp (SAD) b) Cmr: (SAC) vuông góc mp (SBD) c) Tính góc giữa SC v à mp (ABCD) d) Tính góc giữa mp ( SAB) và mp (SBC). e) Tính khoảng cách từ A đến mp ( SBD)
a: CD vuông góc AD; CD vuông góc SA
=>CD vuông góc (SAD)
b: BD vuông góc AC; BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
Đúng 0
Bình luận (0)