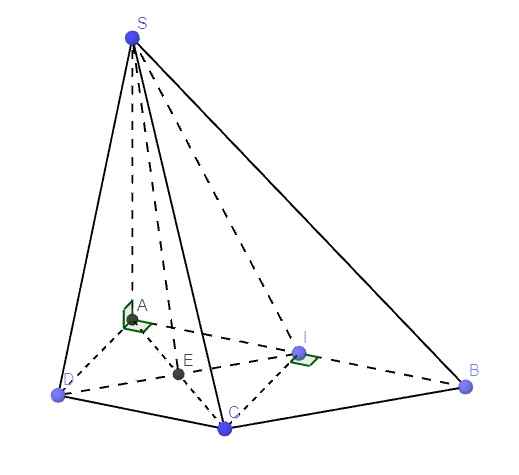
c.
Từ câu b ta có AICD là hình vuông \(\Rightarrow CI\perp AB\)
Mà \(SA\perp\left(ABCD\right)\Rightarrow SA\perp CI\)
\(\Rightarrow CI\perp\left(SAB\right)\)
Lại có \(CI\in\left(SCI\right)\Rightarrow\left(SCI\right)\perp\left(SAB\right)\)
d.
I là trung điểm AB \(\Rightarrow CI\) là trung tuyến ứng với AB
Lại có \(CI=AD=a\) (AICD là hình vuông) \(\Rightarrow CI=\dfrac{1}{2}AB\)
\(\Rightarrow\Delta ACB\) vuông tại C
\(\Rightarrow BC\perp AC\) (1)
Mà \(SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\) (2)
(1);(2) \(\Rightarrow BC\perp\left(SAC\right)\)
\(BC\in\left(SBC\right)\Rightarrow\left(SBC\right)\perp\left(SAC\right)\)
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
Mà \(CD=\left(SCD\right)\cap\left(ABCD\right)\)
\(\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và (ABCD)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\sqrt{3}\Rightarrow\widehat{SDA}=60^0\)
b.
Gọi E là giao điểm AC và DI
I là trung điểm AB \(\Rightarrow AI=\dfrac{1}{2}AB=a\Rightarrow AI=DC\)
\(\Rightarrow AICD\) là hình bình hành
Mà \(\widehat{A}=90^0\Rightarrow AICD\) là hình chữ nhật
\(AI=AD=a\) (hai cạnh kề bằng nhau) \(\Rightarrow AICD\) là hình vuông
\(\Rightarrow AC\perp DI\) tại E
Lại có \(SA\perp\left(ABCD\right)\Rightarrow SA\perp DI\Rightarrow DI\perp\left(SAE\right)\)
Mà \(DI=\left(SDI\right)\cap\left(ABCD\right)\Rightarrow\widehat{SEA}\) là góc giữa (SDI) và (ABCD)
\(AE=\dfrac{1}{2}AC=\dfrac{1}{2}\sqrt{AD^2+CD^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow tan\widehat{SEA}=\dfrac{SA}{AE}=\dfrac{\sqrt{6}}{2}\Rightarrow\widehat{SEA}\approx50^046'\)
Sửa lại kết quả câu b dòng cuối cùng:
\(tan\widehat{SEA}=\dfrac{SA}{AE}=\sqrt{6}\Rightarrow\widehat{SEA}\approx67^047'\)