cho góc xOy có Oz là phân giác. Trên Oz lấy điểm M, từ M kẻ MA\(\perp\)Ox,MB\(\perp\)Oy Chứng Minh: a)MA = MB b)Tam giác OAB là tam giác cân

Những câu hỏi liên quan
Cho góc nhọn xOy . Trên tia phân giác Ot của góc xOy lấy điểm M . Từ M hạ các đường vuông góc MA \(\perp\)Ox và MB \(\perp\)Oy ( A \(\in\)Ox ; B \(\in\)Oy )
a) Chứng minh rằng tam giác OMA = tam giác OMB
b) Chứng minh rằng 2 tam giác OAB và MAB là 2 tam giác cân
Cho góc xOy, kẻ tia phân giác Oz của xOy.Trên Ox lấy điểm A,trên Oy lấy điểm B sao cho OA=OB .Trên Oz lấy điểm M. Kẻ tia MH vuông góc Ox, MK vuông góc Oy ; Nối MA và MB . Chứng minh tam giác MAH=tam giác MBK. (cần vẽ hình và giải đáp ) giúp mik giải nhan :< !
Xét ΔOAM và ΔOBM có
OA=OB
\(\widehat{AOM}=\widehat{BOM}\)
OM chung
Do đó: ΔOAM=ΔOBM
Suy ra: MA=MB
Xét ΔOKM vuông tại K và ΔOHM vuông tại H có
OM chung
\(\widehat{KOM}=\widehat{HOM}\)
Do đó;ΔOKM=ΔOHM
Suy ra: OH=OK
=>AH=BK
Xét ΔMAH vuông tại H và ΔMBK vuông tại K có
MA=MB
AH=BK
Do đó: ΔMHA=ΔMKB
Đúng 2
Bình luận (0)
vẽ góc xOy, Oz là tia phân giác của góc xOy, lấy điểm M bất kì thuộc Oz. Từ M kẻ MA vuông góc với Ox,MB vuông góc với Oy. Chứng minh MA=MB
Vì Oz là tia phân giác của góc xOy
=>góc AOM = góc BOM
VÌ MA\(\perp\)Ox =>góc MAO=90o
MB \(\perp\)Oy =>góc MBO=90o
Xét \(\Delta AOM\)và \(\Delta BOM\)có:
Góc MAO= Góc MBO(Cùng bằng 90o)
OM:cạnh chung
Góc AOM = góc BOM
=>\(\Delta AOM=\Delta BOM\left(Ch-gn\right)\)
=>MA=MB(các cạnh tương ứng)
Đúng 1
Bình luận (0)
cho góc nhọn xOy. GỌi Oz là tia phân giác góc xOy
trên tia Oz lấy điểm M (M ∉O)
Từ M kẻ MA⊥Ox kẻ MB⊥Oy
CM:
a) tam giác MOA=tam giác MOB
b) tam giác AOB là tam giác cân
c) AB⊥Oz
oooõmg cíu t vs !!!
a: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có
OM chung
góc AOM=góc BOM
=>ΔOAM=ΔOBM
b: ΔOAM=ΔOBM
=>OA=OB và MA=MB
=>ΔOAB cân tại O
c: OA=OB
MA=MB
=>OM là trung trực của BA
=>Oz vuông góc BA
Đúng 0
Bình luận (0)
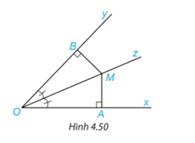
Cho Oz là tia phân giác của góc xOy. Lấy điểm M trên tia Oz và hai điểm A, B lần lượt trên các tia Ox, Oy sao cho MA vuông góc với Ox, MB vuông góc với Oy(H.4.50). Chứng minh rằng MA = MB.
Xét hai tam giác vuông OBM và OAM có:
OM chung
\(\widehat {BOM} = \widehat {AOM}\) (gt)
\( \Rightarrow \Delta OBM = \Delta OAM\)(cạnh huyền – góc nhọn)
Suy ra MB=MA ( 2 cạnh tương ứng)
Đúng 1
Bình luận (0)
Cho góc XOY nhọn. M là một điểm thuộc tia phân giác Oz của góc XOy. Từ M kẻ MA vuông góc Ox tại A, MB vuông góc Oy tại B. Kéo dài AM, BM lần lượt cắt Oy, Ox tại E,F. Chứng minh: a, tam giác OAM = tam giác OBM; MF = ME b, Om vuông góc AB
a: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có
OM chung
\(\widehat{AOM}=\widehat{BOM}\)
Do đó: ΔOAM=ΔOBM
=>MA=MB
Xét ΔMAF vuông tại A và ΔMBE vuông tại B có
MA=MB
\(\widehat{AMF}=\widehat{BME}\)
Do đó: ΔMAF=ΔMBE
=>MF=ME
b:
Ta có: OA=OB
=>O nằm trên đường trung trực của BA(1)
Ta có: MA=MB
=>M nằm trên đường trung trực của BA(2)
Từ (1) và (2) suy ra OM là đường trung trực của BA
=>OM\(\perp\)BA
Đúng 0
Bình luận (0)
Cho góc nh ọn xOy . Gọi M là một điểm trên tia phân giác của góc xOy . Kẻ MA vuông góc với Ox tại A , MB vuông góc với Oy tại B
a) Chứng minh rằng : MA=MB và Tam giác OAB là tam giác cân
b) Chừng minh rằng : MD=ME
c) Chừng minh rằng : OM vuông góc với DE
Bài 6: Cho góc nhọn xOy. Gọi M là một điểm trên tia phân giác của góc xOy. Kẻ MA vuông
góc với Ox tại A, MB vuông góc với Oy tại B.
a, Chứng minh MA = MB và OAB là tam giác cân?
b, Tia BM cắt Ox tại D, tia AM cắt Oy tại E. Chứng minh MD = ME?
c, Chứng minh OM vuông góc với DE?
Bài 6: Cho góc nhọn xOy. Gọi M là một điểm trên tia phân giác của góc xOy. Kẻ MA vuông
góc với Ox tại A, MB vuông góc với Oy tại B.
a, Chứng minh MA = MB và OAB là tam giác cân?
b, Tia BM cắt Ox tại D, tia AM cắt Oy tại E. Chứng minh MD = ME?
c, Chứng minh OM vuông góc với DE?
a, Xét △OAM vuông tại A và △OBM vuông tại B
Có: AOM = BOM (gt)
OM là cạnh chung
=> △OAM = △OBM (ch-gn)
=> AM = BM (2 cạnh tương ứng)
và OA = OB (2 cạnh tương ứng)
=> △OAB cân tại O
b, Xét △MAD vuông tại A và △MBE vuông tại B
Có: AM = MB (cmt)
AMD = BME (2 góc đối đỉnh)
=> △MAD = △MBE (cgv-gnk)
=> MD = ME (2 cạnh tương ứng)
c, Gọi OM ∩ DE = { I }
Ta có: OA + AD = OD và OB + BE = OE
Mà OA = OB (cmt) , AD = BE (△MAD = △MBE)
=> OD = OE
Xét △IOD và △IOE
Có: OD = OE (cmt)
DOI = EOI (gt)
OI là cạnh chung
=> △IOD = △IOE (c.g.c)
=> OID = OIE (2 góc tương ứng)
Mà OID + OIE = 180o (2 góc kề bù)
=> OID = OIE = 180o : 2 = 90o
=> OI ⊥ DE
Mà OM ∩ DE = { I }
=> OM ⊥ DE














