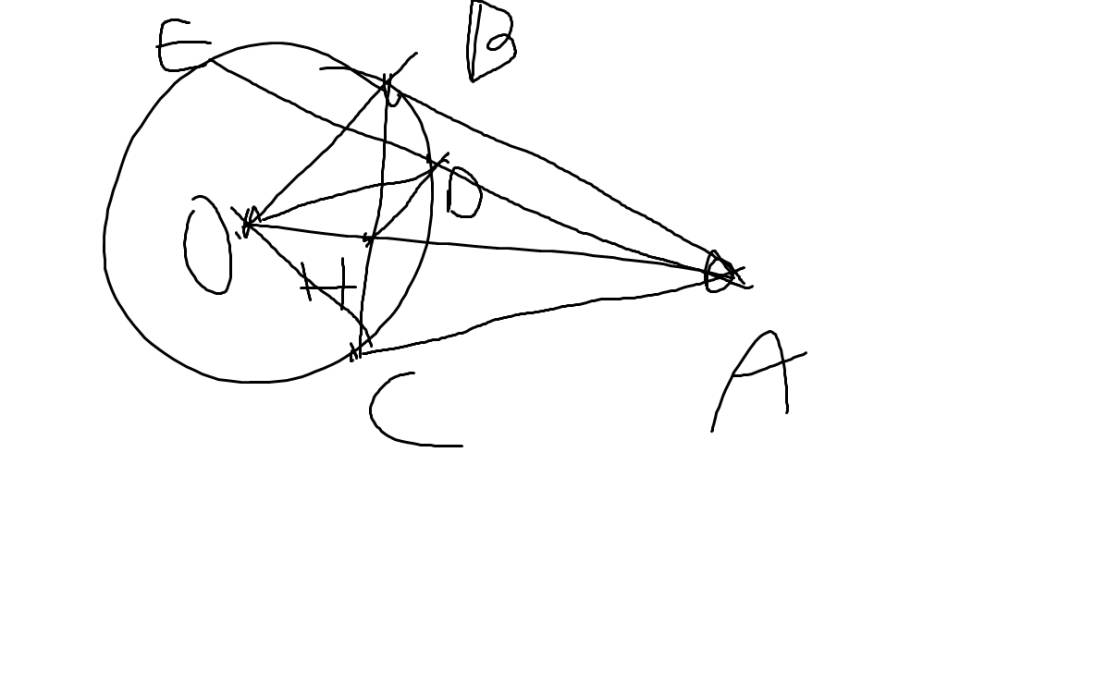
Câu 6: Từ một điểm A ở ngoài đường tròn(O;R),vẽ hai tiếp tuyến AB,AC với đường tròn(B,C là tiếp điểm).
a)Chứng minh OA vuông góc với BC
b)Chứng minh 4 điểm A,B,O,C cùng thuộc một đường tròn
c) Đường thẳng AO cắt đường tròn tại 2 điểm M,N(M nằm giữa A và O),đường thẳng BC cắt AO tại H.Chứng minh AH.AO=AM.AN
d)Khi AO =2R,chứng minh NB là tiếp tuyến của đường tròn đường kính AO