
Những câu hỏi liên quan
1. Cho M(3;-1) và đường thẳng d: 3x-4y+120. Tìm N đối xứng với M qua d.2. Cho M(8;2) và đường thẳng d: 2x-3y+30. Tìm N đối xứng với M qua d.3. Cho đường thẳng d: x+y-50 và I(2;0). Tìm điểm M thuộc d sao cho MI3.4. Cho tam giác ABC có M(2;-1) là trung điểm AB. Đường trung tuyến và đường cao qua A lần lượt là: d1: x+y-70 và d2: 5x+3y-290.a.Tìm điểm A và viết pt cạnh BC.b. Viết pt cạnh AC.CÁC BẠN GIẢI GIÚP MÌNH VỚI NHÉ. CẢM ƠN
Đọc tiếp
1. Cho M(3;-1) và đường thẳng d: 3x-4y+12=0. Tìm N đối xứng với M qua d.
2. Cho M(8;2) và đường thẳng d: 2x-3y+3=0. Tìm N đối xứng với M qua d.
3. Cho đường thẳng d: x+y-5=0 và I(2;0). Tìm điểm M thuộc d sao cho MI=3.
4. Cho tam giác ABC có M(2;-1) là trung điểm AB. Đường trung tuyến và đường cao qua A lần lượt là: d1: x+y-7=0 và d2: 5x+3y-29=0.
a.Tìm điểm A và viết pt cạnh BC.
b. Viết pt cạnh AC.
CÁC BẠN GIẢI GIÚP MÌNH VỚI NHÉ. CẢM ƠN
trl ; bạn kia đúng r
-
_
----------------
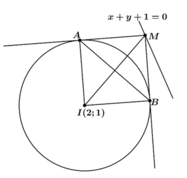
Trong mặt phẳng với hệ tọa độ Oxy. Cho đường tròn (C) : x2+ y2- 4x -2y -1 0 và đường thẳng d: x+ y+1 0. Tìm những điểm M thuộc đường thẳng d sao cho từ điểm M kẻ được đến (C) hai tiếp tuyến hợp với nhau góc 900.
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy. Cho đường tròn (C) : x2+ y2- 4x -2y -1= 0 và đường thẳng d: x+ y+1= 0. Tìm những điểm M thuộc đường thẳng d sao cho từ điểm M kẻ được đến (C) hai tiếp tuyến hợp với nhau góc 900.
![]()
![]()
![]()
Đáp án A
- Do M thuộc d suy ra M( t; -1-t).
Nếu 2 tiếp tuyến vuông góc với nhau thì MAIB là hình vuông
(A; B là 2 tiếp điểm).
Do đó:
![]()
- Ta có :
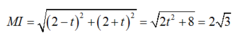
- Do đó : 2t2+ 8= 12
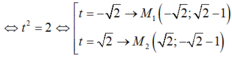
Đúng 0
Bình luận (0)
Cho A(1,2) B(-3,5) d 2x-3y+6=0
(∆) {x=6t ;y =2+4t
Tìm M thuộc (∆) sao cho NA2 + NB2 nhỏ nhất
Chắc là N? Vì M mà sao đằng sau lại là \(NA^2+NB^2\)?
Do N thuộc \(\Delta\) nên tọa độ có dạng \(N\left(6t;4t+2\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AN}=\left(6t-1;4t\right)\\\overrightarrow{BN}=\left(6t+3;4t-3\right)\end{matrix}\right.\)
\(\Rightarrow NA^2+NB^2=\left(6t-1\right)^2+16t^2+\left(6t+3\right)^2+\left(4t-3\right)^2=104t^2+19\ge19\)
Dấu "=" xảy ra khi \(t=0\Rightarrow N\left(0;2\right)\)
Đúng 1
Bình luận (1)
cho đường tròn (C) : x^2+y^2-2x+6y+1=0 , và d :2x-y+3=0. tìm tọa độ M thuộc (C), N thuộc d sao cho M,N đối xứng qua trục hoành
Cho đường tròn (C): x^2 + y^2 +10x-8y+1=0 và d:-x+y-5=0
a) Qua điểm M thuộc d kẻ tiếp tuyến MA,MB
Tìm M sao cho diện tích tam giác IAB lớn nhất (I là tâm đường tròn)
b) Tim P thuộc d sao cho diện tích PAI=3, A tiếp điểm các tiếp tuyến từ P.
Trong mặt phẳng với hệ tọa độ Oxy. Cho đường tròn (C): x2+y2-4x-2y-1=0 và đường thẳng d: x+y+1=0. Tìm những điểm M thuộc đường thẳng d sao cho từ điểm M kẻ được đến (C) hai tiếp tuyến hợp với nhau góc 90 độ
trong mặt phẳng tọa độ Oxy, cho điểm M (-1;2) và đường thẳng d: 4x-3y+5=0. Tìm tọa độ điểm N thuộc đường thẳng d và cách điểm N một khoảng bằng 1
d: 4x-3y+5=0
=>VTPT là (4;-3) và (d) đi qua A(1;3)
=>VTCP là (3;4)
PTTS là:
x=1+3t và y=3+4t
=>N(3t+1;4t+3)
NM=1
=>\(\sqrt{\left(3t+1+1\right)^2+\left(4t+3-2\right)^2}=1\)
=>9t^2+12t+4+16t^2+8t+1=1
=>25t^2+20t+4=0
=>(5t+2)^2=0
=>t=-2/5
=>N(-1/5;-3/5)
Đúng 0
Bình luận (0)
Cho đường thẳng (d) : y = - 2x + 1
a. Điểm nào sau đây thuộc (d):: M(– 1; 3) ; N(1 ; 1) ; K(- 1 /2 ; 0)
b. Tìm toạ độ điểm E thuộc (d)biết Xe = – 2
c.Tìm toạ độ điểm F thuộc(d) biết Yf = 3
d. Cho điểm A( m – 1; 2) thuộc (d) . Tính m ?
b: Thay x=-2 vào (d), ta được:
y=4+1=5
Đúng 1
Bình luận (0)
Cho 3 điểm A(2;-1), B(1;0),C(-1;3) và đường thẳng d: 2x-3y+5=0
1. Tìm D thuộc d sao cho DA= d(D;BC)
2. Tìm H là hình chiếu của A trên d
3. Tìm A' đối xứng A qua d
4 Tìm M thuộc d: MA + MB nhỏ nhất















