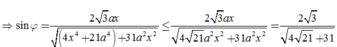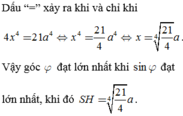Những câu hỏi liên quan
Cho hình thoi ABCD có góc A=60 độ, AB=10cm. Tính diện tích hình thoi ABCD.
Kẻ BH vuông góc AD
Tam giác ABH là tam giác đều nên BH=AD=10(cm)
Suy ra SABCD=10.10=100(cm2)
Cho hình chóp S ABCD . có đáy là hình thoi cạnh a, hình chiếu vuông góc của S trên mặt
phẳng ABCD là trung điểm cạnh = AB ABD=60 và SC hợp với đáy một góc 0 60 . Tính
thể tích V của khối chóp S ABCD
Gọi H là trung điểm AB \(\Rightarrow SH\perp\left(ABCD\right)\)
\(\Rightarrow\) CH là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCH}=60^0\)
Do \(\widehat{ABD}=60^0\Rightarrow\) các tam giác ABD và BCD là tam giác đều cạnh a
\(\Rightarrow\widehat{ABC}=120^0\)
Áp dụng định lý hàm cos cho tam giác BCH:
\(CH=\sqrt{BC^2+BH^2-2BC.BH.cos120^0}=\dfrac{a\sqrt{7}}{2}\)
\(\Rightarrow SH=CH.tan60^0=\dfrac{a\sqrt{21}}{2}\)
\(V=\dfrac{1}{3}SH.2S_{ABD}=\dfrac{1}{3}.\dfrac{a\sqrt{21}}{2}.2.\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^3\sqrt{7}}{8}\)
Đúng 0
Bình luận (0)
Cho hình chóp S. ABCD có đáy ABCD là hình thoi, AB= 2a, góc BAD= 120 độ. Hình chiếu vuông góc của S xuống ( ABCD) trùng với giao điểm I của 2 đường chéo và SI= a/2. Tính góc giữa (SAB) và mặt đáy
Cho hình chóp S.ABCD có ABCD là hình thoi tâm O cạnh a, góc ABC = 60 độ. Hình chiếu vuông góc của S lên (ABCD) là trung điểm của OB, SC tạo với (ABCD) góc 60 độ. Gọi M là trung điểm CD. Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng AM và SB
a )
Cho hình thoi ABCD, góc A= 60°, trên các cạnh AB, BC lấy điểm M, N sao cho BM+BN=AB.
CMR: đường trung trực của MN luôn đi qua một điểm cố định
b ) Hình thoi ABCD có góc A bằng 30 độ, đường cao BH=1,5cm . Tính chu vi hình thoi.
1.Cho hình thoi ABCD có cạnh =a.Biết góc B=60 độ
a)C/m tam giác ABC đều
b)Tính diện tích hình thoi ABCD theo a
2.Cho hình vuông ABCD có độ dài cạnh =a.Điểm M bất kì trên đường thẳng AC.Kẻ ME vuông góc AB tại E và MF vuông góc AC tại F.Tìm vị trí của điểm M trên AC để diện tích tam giác CEF lớn nhất
1) hình tự vẽ nhé
a) Vì ABCD là hình thoi (gt)
\(\Rightarrow AB=BC\left(đn\right)\)
\(\Rightarrow\Delta ABC\)cân tại B
Mà \(\widehat{B}=60^0\)
\(\Rightarrow\Delta ABC\)là tam giác đều
b) Vì \(\Delta ABC\)đều(cmt)\(\Rightarrow AB=BC=AC=a\)
Gọi O là giao điểm 2 đường chéo BD và AC
Vì ABCD là hình thoi (gt) \(\Rightarrow DB\perp AC\left(tc\right)\)
\(\Rightarrow BO\perp AC\)
Vì tam giác ABC đều mà trong tam giác ABC thì BO là đường cao ứng với cạnh AC
\(\Rightarrow BO\)là đường trung tuyến ứng vs cạnh AC(tc)
\(\Rightarrow O\)là trung điểm của AC
\(\Rightarrow AO=OC=\frac{1}{2}AC=\frac{1}{2}a\)
Áp dụng định lý Py-ta-go vào tam giác BOC vuông tại O ta được:
\(BO^2+OC^2=BC^2\)
\(BO^2+\frac{1}{4}a^2=a^2\)
\(BO^2=\frac{3}{4}a^2\)
\(\Rightarrow BO=\frac{\sqrt{3}}{2}a\)
Ta có: \(S_{ABC}=\frac{1}{2}BO.AC=\frac{1}{2}.\frac{\sqrt{3}a}{2}.a\)
\(=\frac{\sqrt{3}}{4}a^2\)
CMTT \(S_{ADC}=\frac{\sqrt{3}}{4}a^2\)
\(S_{ABCD}=S_{ADC}+S_{ABC}=\frac{\sqrt{3}}{2}a^2\)
cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a góc abc=60• .SA vuông góc với mặt phẳng đáy. Tính:
a) d(A; (SBD))
b) d(C; (SAB))
Xem chi tiết
Đề thiếu dữ liệu để xác định độ dài SA rồi bạn
Đúng 0
Bình luận (0)
Cho hình thoi ABCD có
B
A
D
^
60
°
,
A
B
2
a
. Gọi H là trung điểm của AB. Trên đường thẳng d vuông góc với mặt phẳng (ABCD) tại H lấy điểm S thay đổi khác H. Trên tia đối của tia BC lấy điểm M sao cho
B
M
1
4
B
C
. Tính theo a độ dài của SH để góc...
Đọc tiếp
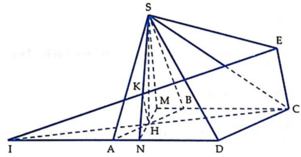
Cho hình thoi ABCD có B A D ^ = 60 ° , A B = 2 a . Gọi H là trung điểm của AB. Trên đường thẳng d vuông góc với mặt phẳng (ABCD) tại H lấy điểm S thay đổi khác H. Trên tia đối của tia BC lấy điểm M sao cho B M = 1 4 B C . Tính theo a độ dài của SH để góc giữa SC và (SAD) có số đo lớn nhất
A. S H = 21 4 4 a .
B. S H = 21 4 4 a .
C. S H = 21 4 a .
D. S H = 21 4 a .
Đáp án A
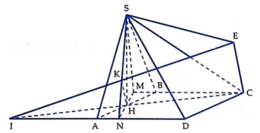
Gọi φ là góc giữa SC và (SAD), N là giao điểm của HM và AD, K là hình chiếu vuông góc của H trên SN, I là giao điểm của HC với AD. Gọi E là điểm đối xứng với I qua K.
Ta có M B = 1 4 B C = a 2 , H B = a , H B M ^ = B A D ^ = 60 °
⇒ H M = H B 2 + M B 2 − 2 H B . M B . c o s H B M ^
⇒ H M = a 2 + a 2 4 − 2 a . a 2 . cos 60 ° = 3 2 a
⇒ H M 2 + M B 2 = 3 2 a 2 + a 2 2 = a 2 = H B 2
⇒ Δ H M B vuông tại M
⇒ H M ⊥ M B hay M N ⊥ B C .
Vì S H ⊥ A D do S H ⊥ A B C D M N ⊥ A D do M N ⊥ B C ⇒ A D ⊥ S M N ⇒ A D ⊥ H K , mà H K ⊥ S N nên H K ⊥ S A D . Lại có HK là đường trung bình của Δ I C E nên H K // C E . Suy ra C E ⊥ S A D tại E và SE là hình chiếu của SC trên mặt phẳng (SAD).
Vậy φ = S C , S A D ^ = S C , S E ^ = C S E ^ .
Đặt S H = x , x > 0 . Do Δ S H N vuông tại H có HK là đường cao nên ta có
1 H K 2 = 1 S H 2 + 1 H N 2 ⇒ H K = S H . H N S H 2 + H N 2 = 3 a x 4 x 2 + 3 a 2 ⇒ C E = 2 H K = 2 3 a x 4 x 2 + 3 a 2
Do Δ S H C vuông tại H nên
S C = S H 2 + H C 2 = S H 2 + H M 2 + M C 2 = x 2 + 3 2 a 2 + 5 a 2 2 = x 2 + 7 a 2
Δ S E C vuông tại E nên sin φ = sin C S E ^ = E C S C = 2 3 a x 4 x 2 + 3 a 2 x 2 + 7 a 2
⇒ sin φ = 2 3 a x 4 x 4 + 21 a 4 + 31 a 2 x 2 ≤ 2 3 a x 4 21 a 2 x 2 + 31 a 2 x 2 = 2 3 4 21 + 31
Dấu “=” xảy ra khi và chỉ khi 4 x 4 = 21 a 4 ⇔ x 4 = 21 4 a 4 ⇔ x = 21 4 4 a .
Vậy góc φ đạt lớn nhất khi sin φ đạt lớn nhất, khi đó S H = 21 4 4 a
Đúng 0
Bình luận (0)
Cho hình thoi ABCD có
B
A
D
^
60
°
,
A
B
2
a
. Gọi H là trung điểm của AB. Trên đường thẳng d vuông góc với mặt phẳng (ABCD) tại H lấy điểm S thay đổi khác H. Trên tia đối của tia BC lấy điểm M sao cho
B
M
1
4
B
C
. Tính theo a độ dài của SH để góc...
Đọc tiếp
Cho hình thoi ABCD có B A D ^ = 60 ° , A B = 2 a . Gọi H là trung điểm của AB. Trên đường thẳng d vuông góc với mặt phẳng (ABCD) tại H lấy điểm S thay đổi khác H. Trên tia đối của tia BC lấy điểm M sao cho B M = 1 4 B C . Tính theo a độ dài của SH để góc giữa SC và (SAD) có số đo lớn nhất
A. S H = 21 4 4 a .
B. S H = 21 4 4 a .
C. S H = 21 4 a .
D. S H = 21 4 a .