a: \(AC=\sqrt{5^2-3^2}=4\left(cm\right)\)

\(AD=\dfrac{2\cdot3\cdot4}{3+4}\cdot cos45=\dfrac{12}{7}\sqrt{2}\left(cm\right)\)

b: Sửa đề: vuông góc AC

Xét ΔABC vuông tại A và ΔHDC vuông tại H có

góc C chung

=>ΔABC đồng dạng với ΔHDC

Xét tam giác NAD và tam giác NBD

có AD=DB(GT)

góc ADN=góc NDB = 90⁰

ND chung

suy ra  tam giác NAD = tam giác NBD (c.g.c)

b) Xét tam giác MAN và tam giác MNB

có MA=MB (GT)

AN=NB (GT)

MN chung

suy ra tam giác MAN = tam giác MNB (c.c.c)

c) theo câu b tam giác MAN = tam giác MNB (c.c.c) suy ra góc AND = góc BND

suy ra ND là tia phân giác của góc ANB

d) góc AMD là góc ngoài tại đỉnh N của tam giác AMN suy ra góc AMD> góc AND 

góc BMD là góc ngoài tại đỉnh N của tam giác BMN suy ra góc BMD> góc BND 

suy ra góc AMD + góc BMD > góc AND + góc BND

hay góc AMB > góc ANB

GiẢi

a , Xét tam giác MNA và tam giác DNA có :

NM=ND (GT)

Góc NMA = góc NDA =90 độ

NA là cạnh chung

=> Tam giác MNA = tam giác DNA (c.g.c)

=> Góc MNA =góc DNA ( hai góc tương ứng)

=. NA là tia phân giác của góc MNP

b, Tam giác MND là tâm giác đều vì mỗi góc đều có só đo = 60 độ

d,Xetstam giác MBA và tam giác DPA có :

BM=DP(GT)

góc MAB = góc DPA ( đối đỉnh)

MA=DA (hai cạnh tương ứng của tam giác MNA=tam giác DNA)

=> Tam giác MBA = tam giác DPA (c.g.c)

=> AB=PA ( hai cạnh tương ứng)

=> Tam giác APB cận tại A

e, AD vuông góc với NP

BD vuông góc với NP

=. D,A,B thẳng hàng

a) Xét ΔNAM vuông tại M và ΔNDA vuông tại D có 

NA chung

NA=ND(gt)

Do đó: ΔNAM=ΔNDA(cạnh huyền-cạnh góc vuông)

⇒\(\widehat{MNA}=\widehat{DNA}\)(hai góc tương ứng)

mà tia NA nằm giữa hai tia NM,NDnên NA là tia phân giác của \(\widehat{NMD}\)hay NA là tia phan giác của \(\widehat{NMP}\)(đpcm)b) Xét ΔNMD có NM=ND(gt)nên ΔNMD cân tại N(Định nghĩa tam giác cân)Xét ΔNMD cân tại N có \(\widehat{MND}=60^0\)(gt)nên ΔNMD đều(Dấu hiệu nhận biết tam giác đều)c) Ta có: ΔNMP vuông tại M(gt)nên \(\widehat{NMP}+\widehat{MPN}=90^0\)(hai góc nhọn phụ nhau)\(\Leftrightarrow\widehat{MPN}=90^0-\widehat{NMP}=90^0-60^0=30^0\)(1)Ta có: NA là tia phân giác của \(\widehat{MNP}\)(cmt)nên \(\widehat{PNA}=\dfrac{\widehat{MNP}}{2}=\dfrac{60^0}{2}=30^0\)(2)Từ (1) và (2) suy ra \(\widehat{APN}=\widehat{ANP}\)Xét ΔANP có \(\widehat{APN}=\widehat{ANP}\)(cmt)nên ΔANP cân tại A(Định lí đảo của tam giác cân)Ta có: ΔANP cân tại A(gt)mà AD là đường cao ứng với cạnh đáy NP(gt)nên AD là đường trung tuyến ứng với cạnh NP(Định lí tam giác cân)hay D là trung điểm của NP(đpcm)

Hình như câu d sai đề

Bạn tự vẽ hình nha

a) xét ∆NAD và ∆NBD có

        ND cạnh chung

     AD=AB   (d là trung điểm của AB )

      Góc NDA = góc NDB(=90°)

=>∆NAD=∆NBD(C-G-C)

b) xét ∆MNA và ∆MNB có

       MN cạnh chung

     Góc MNA = góc MNB (vì ∆NAD=∆NBD )

       NA =NB (vì ∆NAD=∆NBD)

=>∆MNA=∆MNB(c-g-c)

c) ta có ∆NAD=∆NBD (cmt)

 =>góc AND =góc BND (2 GÓC TƯƠNG ỨNG )

 =>ND LÀ TIA PHÂN GIÁC CỦA GÓC ANB

       

Hình bạn tự vẽ nhé

a. Xét hai tam giác vuông MND và tam giác vuông HND có

               góc NMD = góc NHD = 90độ

               cạnh ND chung

              góc MND = góc HND [ vì ND là pg góc N ]

Do đó ; tam giác MND = tam giác HND [ cạnh huyền - góc nhọn ]

\(\Rightarrow\) MD = HD 

b. Theo câu a ; tam giác MND = tam giác HND 

\(\Rightarrow\)góc MDN = góc HDN 

HỌC TỐT

a,xét hai tam giác :tam giác NDM và tam giác NDH

có :ND là cạnh chung

     góc N1=góc N2

Do đó tam giác NDM=tam giác NDH (cạnh huyền -góc nhọn)

b,Theo câu a,tam giác NDM=tam giác NDH

                     => Góc MDN=góc HDN

                                            

Đồng dạng theo TH góc góc 
góc HCD= góc NBH(Phụ HCB)
góc DHC=góc BHN(Phụ CHN) 

Nhớ k

a) Xét hai tam giác AMH và NMB có:

MA = MN (gt)

MB = MH (M là trung điểm BH)

ˆAMH=ˆBMNAMH^=BMN^ (đối đỉnh)

⇒ΔAMH=ΔNMB(c.g.c)⇒ΔAMH=ΔNMB(c.g.c)

Vì ΔAMH=ΔNMB(c.g.c)ΔAMH=ΔNMB(c.g.c) nên góc H = góc B

Mà ˆH=900H^=900 nên ˆB=ˆH=900B^=H^=900 (yttu)

Do đó 

b) Ta có AH = NB (do ΔAMH=ΔNMB(c.g.c)ΔAMH=ΔNMB(c.g.c))

Vì AH là đường cao của tam giác cân ABC nên AH < AB 

Do đó NB < AB

c) Ta có ˆMAH=ˆMNBMAH^=MNB^ (do ΔAMH=ΔNMB(c.g.c)ΔAMH=ΔNMB(c.g.c))

Vì NB < AB nên góc BAM < góc MNB (quan hệ góc và cạnh đối diện trong tam giác ABN)

Do đó góc BAM < góc MAH

d) Vì tam giác ABC cân tại A có AH vuông BC nên AH đồng thời là đường trung trực BC

Mặt khác, I nằm trên đường trung trực BC nên A, H, I thẳng hàng 

a) Xét ΔAMH và ΔNMB có

MA=MN(gt)

\(\widehat{AMH}=\widehat{NMB}\)(hai góc đối đỉnh)

MH=MB(M là trung điểm của BH)

Do đó: ΔAMH=ΔNMB(c-g-c)

a) Ta có: ΔAMH=ΔNMB(cmt)

nên \(\widehat{AHM}=\widehat{NBM}\)(hai góc tương ứng)

mà \(\widehat{AHM}=90^0\)(AH\(\perp\)BC)

nên \(\widehat{NBM}=90^0\)

hay NB\(\perp\)BC(đpcm)

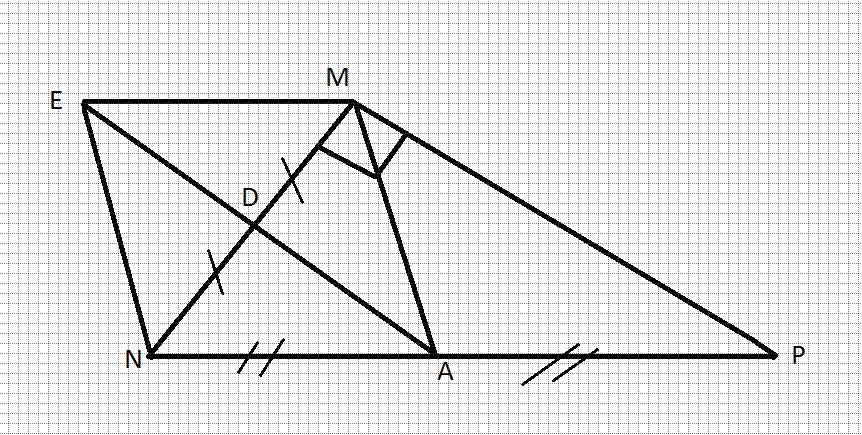
a: Xét ΔMNP có NA/NP=ND/NM

nên DA//MP

=>DA vuông góc với NM

=>EA vuông góc với NM

mà EA cắt NM tại trung điểm của EA

nên E đối xứng A qua MN

b: Xét tứ giác MENA có

D là trung điểm chung của MN và EA

AN=AM

Do đó: MENA là hình thoi