\(|\)x2+2x\(|\)+\(|\)y2-9\(|\)=0
Những câu hỏi liên quan
Cho hai đường tròn
C
1
:
x
2
+
y
2
−
6
x
−
4
y
+
9
0
v
à
C
2
:
x
2
+
y
2
−
2
x
−
8
y
+...
Đọc tiếp
Cho hai đường tròn C 1 : x 2 + y 2 − 6 x − 4 y + 9 = 0 v à C 2 : x 2 + y 2 − 2 x − 8 y + 13 = 0 . Giao điểm của hai đường tròn là
A.A(1; 3), B(2; 4)
B.A(1; 2), B(3; 4)
C.A(1; 4), B(2; 3)
D. Không tồn tại
Tọa độ giao điểm là nghiệm của hệ phương trình
x 2 + y 2 − 6 x − 4 y + 9 = 0 x 2 + y 2 − 2 x − 8 y + 13 = 0 ⇔ x 2 + y 2 − 6 x − 4 y + 9 = 0 − 4 x + 4 y − 4 = 0 ⇔ x 2 + y 2 − 6 x − 4 y + 9 = 0 ( 1 ) x − y + 1 = 0 ( 2 )
Từ (2) suy ra: y = x+ 1 thay vào (1) ta được:
x 2 + ( x + 1 ) 2 - 6 x – 4 ( x + 1 ) + 9 = 0 x 2 + x 2 + 2 x + 1 - 6 x - 4 x – 4 + 9 = 0
2 x 2 – 8 x + 6 = 0
Vậy 2 đường tròn đã cho cắt nhau tại 2 điểm là (1; 2) và (3;4).
ĐÁP ÁN B
Đúng 0
Bình luận (0)
Hãy cho biết phương trình nào trong các phương trình sau đây là phương trình đường tròn:
2x2 + y2 – 8x + 2y – 1 = 0;
x2 + y2 + 2x – 4y – 4 = 0;
x2 + y2 – 2x – 6y + 20 = 0;
x2 + y2 + 6x + 2y + 10 = 0.
+ 2x2 + y2 – 8x + 2y – 1 = 0 không phải phương trình đường tròn vì hệ số của x2 khác hệ số của y2.
+ Phương trình x2 + y2 + 2x – 4y – 4 = 0 có :
a = –1; b = 2; c = –4 ⇒ a2 + b2 – c = 9 > 0
⇒ phương trình trên là phương trình đường tròn.
+ Phương trình x2 + y2 – 2x – 6y + 20 = 0 có :
a = 1; b = 3; c = 20 ⇒ a2 + b2 – c = –10 < 0
⇒ phương trình trên không là phương trình đường tròn.
+ Phương trình x2 + y2 + 6x + 2y + 10 = 0 có :
a = –3; b = –1; c = 10 ⇒ a2 + b2 – c = 0 = 0
⇒ phương trình trên không là phương trình đường tròn.
Đúng 0
Bình luận (0)
c) C x(y2 +z2)+y(z2 +x2)+z(x2 +y2)+2xyz.
d) D x3(y−z)+y3(z−x)+z3(x−y).
e) E (x+y)(x2 −y2)+(y+z)(y2 −z2)+(z+x)(z2 −x2).
b) x2 +2x−24 0.
d) 3x(x+4)−x2 −4x 0.
f) (x−1)(x−3)(x+5)(x+7)−297 0.
(2x−1)2 −(x+3)2 0.
c) x3 −x2 +x+3 0.
e) (x2 +x+1)(x2 +x)−2 0.
a) A x2(y−2z)+y2(z−x)+2z2(x−y)+xyz.
b) B x(y3 +z3)+y(z3 +x3)+z(x3 +y3)+xyz(x+y+z). c) C x(y2 −z2)−y(z2 −x2)+z(x2 −y2).
Đọc tiếp
c) C = x(y2 +z2)+y(z2 +x2)+z(x2 +y2)+2xyz.
d) D = x3(y−z)+y3(z−x)+z3(x−y).
e) E = (x+y)(x2 −y2)+(y+z)(y2 −z2)+(z+x)(z2 −x2).
b) x2 +2x−24 = 0.
d) 3x(x+4)−x2 −4x = 0.
f) (x−1)(x−3)(x+5)(x+7)−297 = 0.
(2x−1)2 −(x+3)2 = 0.
c) x3 −x2 +x+3 = 0.
e) (x2 +x+1)(x2 +x)−2 = 0.
a) A = x2(y−2z)+y2(z−x)+2z2(x−y)+xyz.
b) B = x(y3 +z3)+y(z3 +x3)+z(x3 +y3)+xyz(x+y+z). c) C = x(y2 −z2)−y(z2 −x2)+z(x2 −y2).
Đề bài yêu cầu gì vậy em.
Đúng 0
Bình luận (0)
Vị trí tương đối của hai mặt cầu:
x
2
+
y
2
+
z
2
+ 2x - 2y - 2z - 7 0 và
x
2
+
y
2
+
z
2
+ 2x + 2y + 4z + 5 0 là: A. ở ngoài nhau B. tiếp xúc C. cắt nhau D....
Đọc tiếp
Vị trí tương đối của hai mặt cầu: x 2 + y 2 + z 2 + 2x - 2y - 2z - 7 = 0 và x 2 + y 2 + z 2 + 2x + 2y + 4z + 5 = 0 là:
A. ở ngoài nhau
B. tiếp xúc
C. cắt nhau
D. chứa nhau
Đáp án C
Mặt cầu: x 2 + y 2 + z 2 + 2x - 2y – 2z – 7 = 0 có tâm I(-1; 1;1) và
Mặt cầu: x 2 + y 2 + z 2 + 2x + 2y + 4z + 5= 0 có tâm I’( -1; -1; -2) và R’ = 1
Do đó, hai mặt cầu này cắt nhau.
Đúng 0
Bình luận (0)
3. Tìm x, biết:
a) x3 - 1/9 = 0
b) 2x - 2y - x2 + 2xy - y2 = 0
c) x(x -30 = x - 3 = 0
d) x2 ( x - 3) + 27 - 9x = 0
a,\(x^3-\dfrac{1}{9}=0\)
\(\Rightarrow x^3-\left(\dfrac{1}{3}\right)^3=0\)
\(\Rightarrow\left(x-\dfrac{1}{3}\right)\left(x^2+\dfrac{1}{3}x+\dfrac{1}{9}\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-\dfrac{1}{3}=0\\x^2+\dfrac{1}{3}x+\dfrac{1}{9}=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x^2+\dfrac{1}{3}x=-\dfrac{1}{9}\end{matrix}\right.\)
\(\Rightarrow x=\dfrac{1}{3}\)
Đúng 0
Bình luận (0)
Bài 1 : Tìm x,y
f) x2 + y2 - 2x + 6y + 10 = 0
g) x2 + y2 +1 = xy +x + y
h) 5x2 - 2x.(2 + y ) + y2 +1 = 0
a, (x^2 -2x+1)+(y^2 +6y+9) =0
(x-1)^2 +(y+3)^2 =0
Do đó: x-1=0 và y+3=0
Vậy x=1 và y=-3
b, x^2 +y^2 +1=xy+x+y
2x^2 +2y^2 +2=2xy+2x+2y
2x^2 +2y^2 -2xy-2x-2y +2=0
(x^2 -2x+1)+(y^2 -2y+1)+ (x^2 +y^2 -2xy)=0
(x-1)^2 +(y-1)^2 +(x-y)^2 =0
Suy ra: x-1=0, y-1=0 và x-y=0
Vậy x=1,y=1
c,5x^2 - 4x-2xy+y^2 +1=0
(4x^2 -4x+1)+(x^2 -2xy+y^2 )=0
(2x-1)^2 +(x-y)^2 =0
Do đó: 2x-1 =0 và x=y suy ra: x=0,5 và x=y
Vậy x=y=0,5
Đúng 0
Bình luận (0)
Trong không gian với trục tạo độ Oxyz, cho mặt phẳng (
α
): 2x - 2y + z -3 0 và mặt cầu (S):
x
2
+
y
2
+
z
2
-
2
x
+
4
y
-
6
z
+
9
0
. Khi đó, phát biểu nào sau đây đúng? A. (
α...
Đọc tiếp
Trong không gian với trục tạo độ Oxyz, cho mặt
phẳng ( α ): 2x - 2y + z -3 = 0 và mặt cầu
(S): x 2 + y 2 + z 2 - 2 x + 4 y - 6 z + 9 = 0 . Khi đó,
phát biểu nào sau đây đúng?
A. ( α ) không cắt (S)
B. ( α ) tiếp xúc với (S)
C. ( α ) cắt (S) theo giao tuyến là một đường tròn có bán kính nhỏ hơn bán kính của (S)
D. ( α ) cắt (S) theo giao tuyến là một đường tròn có tâm trùng với tâm của (S)
Đáp án C
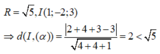
⇒ ( α ) cắt ( β ) theo giao tuyến là một đường tròn có bán kính nhỏ hơn bán kính của (S)
Đúng 0
Bình luận (0)
Trong không gian với trục tọa độ Oxy, cho mặt phẳng
(
α
)
:
2
x
−
2
y
+
z
−
3
0
và mặt cầu
(
S
)
:
x
2
+
y
2
+
z
2
−
2
x
+
4
y
−
6
z
+...
Đọc tiếp
Trong không gian với trục tọa độ Oxy, cho mặt phẳng ( α ) : 2 x − 2 y + z − 3 = 0 và mặt cầu ( S ) : x 2 + y 2 + z 2 − 2 x + 4 y − 6 z + 9 = 0 . Khi đó, phát biểu nào sau đây đúng?
A. ( α ) không cắt (S).
B. ( α ) tiếp xúc với (S).
C. ( α ) cắt theo giao tuyến là một đường tròn có bán kính nhỏ hơn bán kính của (S).
D. ( α ) cắt (S) theo giao tuyến là một đường tròn có tâm trùng với tâm của (S).
Số tiếp tuyến chung của hai đường tròn
(
C
1
)
:
x
2
+
y
2
-
2
x
+
4
y
+
1
0
v
à
(
C
2
)
:
x
2
+
y
2
+
6
x
-
8
y
+
20
0...
Đọc tiếp
Số tiếp tuyến chung của hai đường tròn ( C 1 ) : x 2 + y 2 - 2 x + 4 y + 1 = 0 v à ( C 2 ) : x 2 + y 2 + 6 x - 8 y + 20 = 0
A. 1
B. 2
C. 3
D. 4
