(2x-1).(2y+1)=-35
Tìm số gnuyeen x và y
Những câu hỏi liên quan
tìm các số gnuyeen x,y biết xy+x-2y +3 = 0
=>x(y+1)-2y-2+5=0
=>(x-2)(y+1)=-5
=>\(\left(x-2;y+1\right)\in\left\{\left(1;-5\right);\left(-5;1\right);\left(-1;5\right);\left(5;-1\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(3;-6\right);\left(-3;0\right);\left(1;4\right);\left(7;-2\right)\right\}\)
Đúng 0
Bình luận (0)
Tìm các số thực x và y, biết:
(2x + y) + (2y - x)i = (x - 2y + 3) + (y + 2x + 1)i
(2x + y) + (2y - x)i = (x - 2y + 3) + (y + 2x + 1)i
Đúng 0
Bình luận (0)
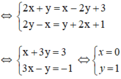
Giải hệ pt:
a)(x+√(x^2+4))(y+√(y^2+1))=2 và 27x^6=x^3-8y+2
b)(8x-3)√(2x-1) -y-4y^3=0 và 4x^2-8x+2y^3+y^2-2y+3=0
c) x(1+y-x)=-2y^2-y và x(√2y -2)=y(√(x-1)-2)
d) √(x+2y)+√(2x-y)+x^2y=√x+√3y+xy^2 và 2(1-y)√(x^2+2y-1)=y^2-2x-1
e)(y-2x+√y-√x)/√xy +1=0 và √(1-xy) +x^2-y^2=0
CÁC BẠN ƠI..GIÚP MK VS Ạ...MAI MK HOK R...CẢM ƠM TRƯỚC Ạ...☺️☺️☺️
a) tìm số tự nhiên x và số nguyên y thỏa mãn: \(x^2y+2xy+x^2-2018x+y=-1\)
b) giải hệ phương trình \(\left\{{}\begin{matrix}x^2-2y^2+xy=2y-2x\\\sqrt{x+2y+1}+\sqrt{x^2+y+2}=4\end{matrix}\right.\)
\(y\left(x+1\right)^2=-x^2+2018x-1\)
\(\Leftrightarrow y=\dfrac{-x^2+2018x-1}{\left(x+1\right)^2}=-1+\dfrac{2020x}{\left(x+1\right)^2}\)
\(\Rightarrow\dfrac{2020x}{\left(x+1\right)^2}\in Z\)
Mà x và \(x\left(x+2x\right)+1\) nguyên tố cùng nhau
\(\Rightarrow2020⋮\left(x+1\right)^2\)
Ta có 2020 chia hết cho đúng 2 số chính phương là 1 và 4
\(\Rightarrow\left[{}\begin{matrix}\left(x+1\right)^2=1\\\left(x+1\right)^2=4\end{matrix}\right.\) \(\Rightarrow x=\left\{0;1\right\}\) \(\Rightarrow y\)
Đúng 1
Bình luận (0)
b.
Từ pt đầu:
\(x^2+xy-2y^2+2\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(x+2y\right)+2\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(x+2y+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=y\\x=-2y-2\end{matrix}\right.\)
Thế xuống dưới ...
Đúng 0
Bình luận (0)
Cho x, y thỏa mãn phương trình: `2x^2+ x = 3y^2` + 1 CMR: x - y và 2x + 2y+ 1 là số chính phương
Tìm các số tự nhiên x và y , sao cho :
a) (2x+1)(y-3)=10 b) (3x-2)(2y-3)=1
c) (x+1)(2y-1)=12 d) x+6=y(x-1)
e) x-3=y(x+2)
cho x+y-2=0
a) A= x^3+x^2y-2x^2-xy-y^2+3y+x-1
b) B= x^3+x^2y-2x^2-x^2y-y^2x+2xy+2y+2x+2
c) C= x^4+2x^3y-2x^3+x^2y^2-2x^2y-x(x+y)+2x+3
2) cho
11...1
a= --------------
n chữ số 1
100...05
b= ------------------
n-1 chữ số 0
CMR: ab+1 là 1 số chính phương
BÀi 2:
Đặt x = 11...1(n chữ số 1), khi đó
a = x
b = 100..05(n-1 chữ số 0) = 100...00(n chữ số 0) + 5
b = 99...9(n chữ số 9) + 1 + 5 = 9x +6
=> \(ab+1=x\left(9x+6\right)+1\)
=> \(ab+1=9x^2+6x+1=\left(3x+1\right)^2\)
Vậy ab + 1 là 1 số chính phương
Đúng 0
Bình luận (0)
Tìm các số thực x, y thỏa mãn:
a) 2x + 1 + (1 – 2y)i = 2 – x + (3y – 2)i
b) 4x + 3 + (3y – 2)i = y +1 + (x – 3)i
c) x + 2y + (2x – y)i = 2x + y + (x + 2y)i
Cho 2 số thực x và y thoả x+y=1 Tính giá trị biểu thức: A=x⁴-2x³-2x²y²-2y³+x²+y²+y⁴