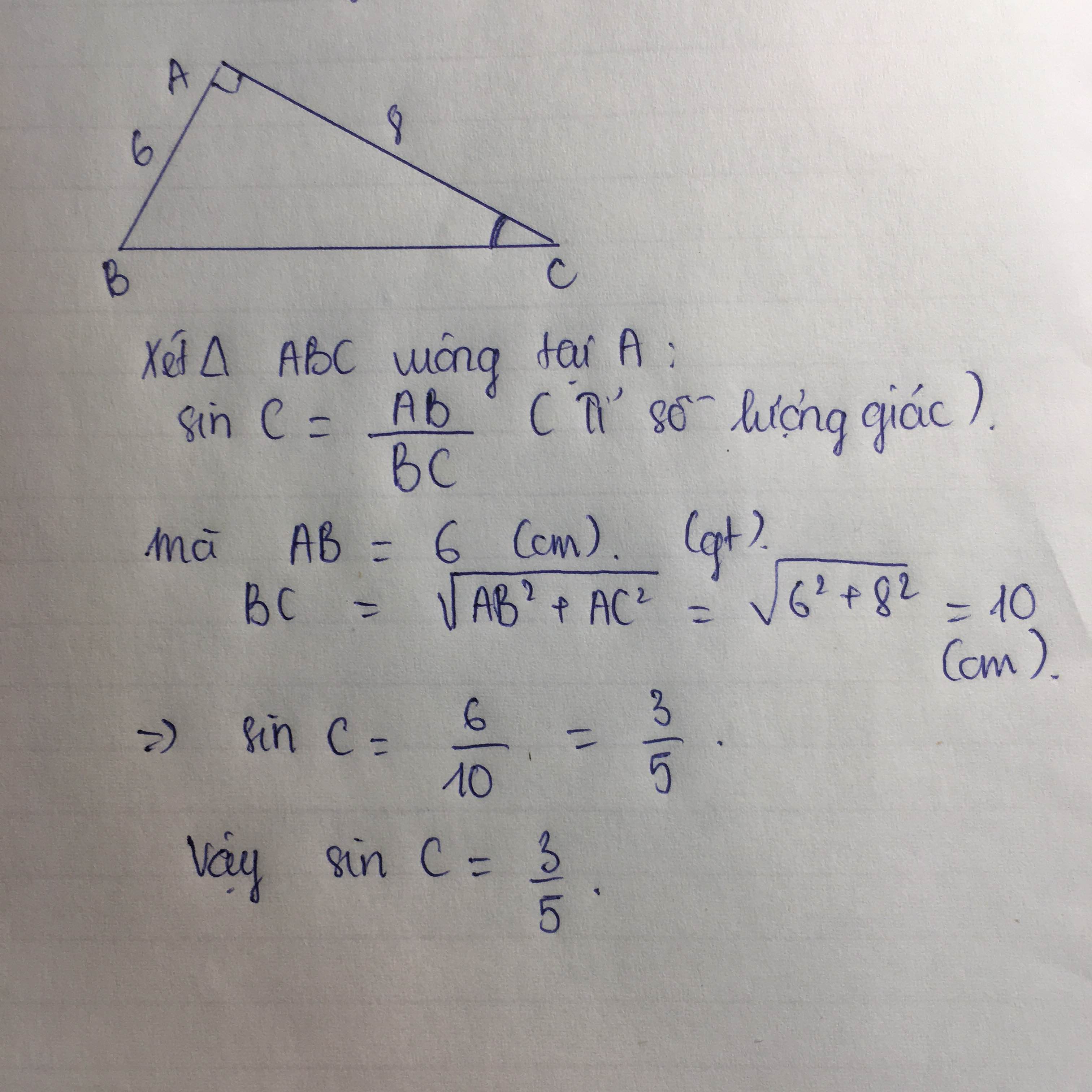BH=12^2/9=16cm

BC=16+9=25cm

AB=căn(16*25)=20cm

AC=căn(9*25)=15cm

sin B=AC/BC=3/5

tan C=AB/AC=20/15=4/3

a/

Xét tg vuông ABC

\(AH^2=BH.HC\) (Trong tg vuông bình phương đường đường cao hạ từ đỉnh góc vuông xuống cạnh huyền bằng tích giữa 2 hình chiếu của 2 cạnh góc vuông trên cạnh huyền)

\(\Rightarrow AH=\sqrt{2.6}=2\sqrt{3}\)

\(BC=BH+HC=2+6=8\)

\(AB^2=BH.BC\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)

\(\Rightarrow AB=\sqrt{2.8}=4\)

b/

Xét tg vuông ABH

\(\sin B=\dfrac{AH}{AB}=\dfrac{2\sqrt{3}}{4}=\dfrac{\sqrt{3}}{2}\)

Xét tg vuông ACH

\(\tan C=\dfrac{AH}{HC}=\dfrac{2\sqrt{3}}{6}=\dfrac{\sqrt{3}}{3}\)

c/

a) \(AH^2=HB.HC=2.6=12\Rightarrow AH=2\sqrt[]{3}\left(cm\right)\)

\(AB^2=AH^2+BH^2=12+4=16\Rightarrow AB=4\left(cm\right)\left(Pitago\right)\)

b) \(SinB=\dfrac{AH}{AB}=\dfrac{2\sqrt[]{3}}{4}=\dfrac{\sqrt[]{3}}{2}\)

\(tanC=\dfrac{AH}{HC}=\dfrac{2\sqrt[]{3}}{6}=\dfrac{\sqrt[]{3}}{3}\)

Câu C bạn xem lại đề

\(AC=\sqrt{BC^2-AB^2}=8\\ \Rightarrow A=\dfrac{\dfrac{AC}{BC}+\dfrac{AB}{BC}}{\dfrac{AB}{AC}+\dfrac{AC}{AB}}=\dfrac{\dfrac{AB+AC}{BC}}{\dfrac{6}{8}+\dfrac{8}{6}}=\dfrac{\dfrac{14}{10}}{\dfrac{25}{12}}=\dfrac{7}{5}\cdot\dfrac{12}{25}=\dfrac{84}{125}\)

Theo định lí Pytago tam giác ABC vuông tại A

\(BC=\sqrt{AB^2+AC^2}=10cm\)

Xét tam giác ABC vuông tại A, đường cao AH 

* Áp dụng hệ thức \(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{48}{10}=\dfrac{24}{5}cm\)

* Áp dụng hệ thức \(AB^2=HB.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{36}{10}=\dfrac{18}{5}cm\)

\(CH=BC-BH=10-\dfrac{18}{5}=\dfrac{32}{5}cm\)

bài này ko đủ dữ kiện. nếu bổ sung dữ kiện thì ta có thể tính dc với cách tính của định lý pitago.những bài này thường có 3 dữ kiện trở lên 

bạn học lớp mấy z

a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC

nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH^2=HB\cdot HC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=2\sqrt{13}\left(cm\right)\\AC=3\sqrt{13}\left(cm\right)\\AH=6\left(cm\right)\end{matrix}\right.\)

Áp dụng định lý Pytago vào ΔABC vuông tại A ta có:

\(BC^2=AB^2+AC^2=6^2+8^2\Leftrightarrow BC=10\left(cm\right)\)

\(\Rightarrow sinC=\dfrac{AB}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\)

Áp dụng định lí Pytago vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)

\(\Leftrightarrow\dfrac{1}{AH^2}=\dfrac{1}{6^2}+\dfrac{1}{8^2}=\dfrac{100}{48^2}\)

\(\Leftrightarrow AH^2=\left(\dfrac{48}{10}\right)^2\)

hay AH=4,8cm

Vậy: AH=4,8cm

BC=10cm

AH=4,8cm

BH=3,6cm

\(\widehat{C}=37^0\)