Tìm b, c để phương trình x 2 + bx + c = 0 có hai nghiệm là những số dưới đây: x 1 = - 1 và x 2 = 2

Những câu hỏi liên quan
Tìm b, c để phương trình x 2 + bx + c = 0 có hai nghiệm là những số dưới đây: x 1 = 1 + 2 và x 2 = 1 - 2
Tìm b, c để phương trình x 2 + bx + c = 0 có hai nghiệm là những số dưới đây: x 1 = - 5 và x 2 = 0
Tìm b, c để phương trình x 2 + bx + c = 0 có hai nghiệm là những số dưới đây: x 1 = 3 và x 2 = - 1 2
Tìm b, c để phương trình \(x^2+bx+c=0\) có hai nghiệm là những số dưới đây :
a) \(x_1=-12,x_2=2\)
b) \(x_1=-5,x_2=0\)
c) \(x_1=1+\sqrt{2},x_2=1-\sqrt{2}\)
d) \(x_1=3,x_2=-\dfrac{1}{2}\)
a: \(\left\{{}\begin{matrix}x_1+x_2=-b\\x_1x_2=c\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=10\\c=-24\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}x_1+x_2=-b\\x_1x_2=c\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-b=-5\\c=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=5\\c=0\end{matrix}\right.\)
c: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=1-2=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2\\c=-1\end{matrix}\right.\)
d: \(\left\{{}\begin{matrix}x_1+x_2=3-\dfrac{1}{2}=\dfrac{5}{2}\\x_1x_2=-\dfrac{3}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-\dfrac{5}{2}\\c=-\dfrac{3}{2}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Tìm a, b, c để phương trình a x 2 + bx + c = 0 có hai nghiệm là x 1 = -2 và x 2 = 3. Có thể tìm được bao nhiêu bộ ba số a, b, c thỏa mãn yêu cầu bài toán?
x = -2 là nghiệm của phương trình: a x 2 + bx + c = 0, ta có:
4a - 2b + c = 0
x = 3 là nghiệm của phương trình: a x 2 + bx + c = 0 ta có:
9a + 3b + c = 0
Ba số a, b, c là nghiệm của hệ phương trình:
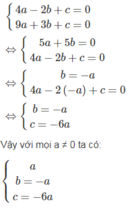
thì phương trình a x 2 + bx + c = 0 có nghiệm x 1 = -2; x 2 = 3
Ví dụ: a = 2, b = -2, c = -12 ta có phương trình:
2 x 2 - 2x - 12 = 0
⇒ x 2 - x - 6 = 0
⇒ (x + 2)(x - 3) = 0
Có nghiệm: x 1 = - 2; x 2 = 3
Có vô số bộ ba a, b, c thỏa mãn yêu cầu bài toán.
Đúng 0
Bình luận (0)
Cho các phương trình \(x^2+bx+c=0\) và \(x^2+b_1.x+c_1=0\)
trong đó b,c,b1, c1 là số nguyên
và (b-b1)2 + (c-c1)2 >0
Chứng minh nếu 2 phương trình có 1 nghiệm chung thì nghiệm thứ 2 của hai phương trình là hai số nguyên phân biệt.
Cho phương trình x² +(m+3)x-2m+2=0 a. Tìm m để phương trình có hai nghiệm trái dấu. b. Tìm m để phương trình có hai nghiệm dương phân biệt. c. Tìm m để phương trình có hai nghiệm âm phân biệt. d. Tìm m để phương trình có ít một nghiệm dương.
Sửa đề: \(x^2+\left(m+3\right)x+2m+2=0\)
a: Để phương trình có hai nghiệm trái dấu thì 2m+2<0
hay m<-1
b: \(\text{Δ}=\left(m+3\right)^2-4\left(2m+2\right)\)
\(=m^2+6m+9-8m-8\)
\(=m^2-2m+1=\left(m-1\right)^2>=0\)
Do đó: Phương trình luôn có hai nghiệm với mọi m
Để phương trình có hai nghiệm dương phân biệt thì \(\left\{{}\begin{matrix}m-1< >0\\2m+2>0\\m+3>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>-1\\m< >1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho phương trình x2+bx+c=0 (*) với b,c là các số thõa mãn 2b+4c=-1
a. chứng tỏ rằng phương trình (*) luôn có nghiệm
b. Tìm b,c biết rằng phương trình (*) có 2 nghiệm x1,x2 với x1-2x2=0
a) đenta=b^2-4c
2b+4c=-1=>c=-1-2b)/4
thay vô chứng minh nó lớn hơn 0
Đúng 0
Bình luận (0)
x1+x2=b
x1x2=c
ta có x1=2x2
thay vô tìm x1;x2 theo b,c rồi thay vô
mk tính được x1=2x;x2=b/3 thay cái này vô x1-2x2=0 tìm ra b
x1=căn(c/2);x2=căn(2c) thay vô cái x1-2x2=0 tìm ra c
Đúng 0
Bình luận (0)
Xét hai câu sau:
P: “Phương trình bậc hai \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt”;
Q: “Phương trình bậc hai \(a{x^2} + bx + c = 0\) có biệt thức \(\Delta = {b^2} - 4ac\;\, > 0\)”.
a) Hãy phát biểu mệnh đề \(P \Rightarrow Q\).
b) Hãy phát biểu mệnh đề \(Q \Rightarrow P\).
Mệnh đề \(P \Rightarrow Q\): “Nếu phương trình bậc hai \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt thì phương trình bậc hai \(a{x^2} + bx + c = 0\) có biệt thức \(\Delta = {b^2} - 4ac\;\, > 0\).”
Mệnh đề \(Q \Rightarrow P\): “Nếu phương trình bậc hai \(a{x^2} + bx + c = 0\) có biệt thức \(\Delta = {b^2} - 4ac\;\, > 0\) thì phương trình bậc hai \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt.”
Đúng 0
Bình luận (0)














