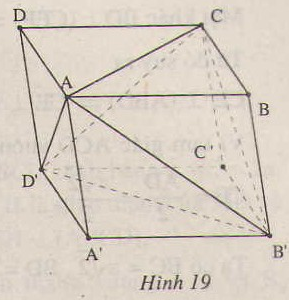
Hình lập phương ABCD.A'B'C'D' cạnh a. Tính thể tích khối tứ diện ACB'D'.
A. a 3 3
B. a 3 2
C. a 3 6
D. a 3 4
Hình lập phương ABCD.A'B'C'D' cạnh a. Tính thể tích khối tứ diện ACB'D'.
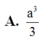
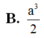
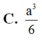
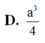
Biết rằng khối tứ diện đều cạnh bằng k thì có thể tích bằng 2 k 3 12 . Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a 2 . Tính theo a thể tích khối tứ diện A C B ' D ' .
A. 2 2 a 3 3
B. 2 a 3 6
C. 2 a 3 2
D. a 3 3
Chọn đáp án A.

Chú ý: Tứ diện đều chỉ là trường hợp đặc biệt của một số tứ diện hoặc một hình chóp tam giác. Chúng ta có các kết quả như sau:
1. Cho khối chóp tam giác đều có cạnh đáy bằng a và cạnh bên bằng b. Thể tích khối chóp tam giác đều bằng
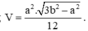
2. Cho khối tứ diện ABCD có và các cạnh còn lại đều bằng a. Thể tích khối tứ diện ABCD là ![]()
3. Cho khối tứ diện ABCD có AB = x, CD = y và các cạnh còn lại đều bằng a. Thể tích khối tứ diện ABCD là
![]()
4. Cho khối tứ diện gần đều ABCD có AB = CD = a, AC = BD = b, AD = BC = c. Thể tích khối tứ diện ABCD là
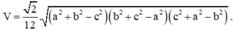
Cho hình lập phương ABCD.A'B'C'D' có cạnh là a. Tính thể tích khối tứ diện ABC'D' theo a?
A. a 2 6
B. a 3 2
C. a 3 4
D. a 3 3
Cho hình lập phương ABCD.A'B'C'D' có cạnh là a. Tính thể tích khối tứ diện ABC'D' theo a?
A. a 3 6
B. a 3 2
C. a 3 4
D. a 3 3
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Tính thể tích V của khối tứ diện AB'C'D'.
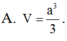
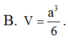
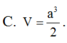
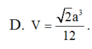
Cho hình lập phương A B C D . A ' B ' C ' D ' cạnh a. Thể tích khối tứ diện A B ' C ' D ' bằng
A. a 3 3
B. a 3 6
C. a 3 2
D. 3 a 3 12
Chọn B.
Phương pháp: Sử dụng công thức tính thể tích khối chóp V = 1 3 B h
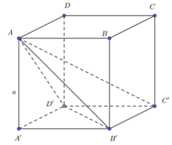
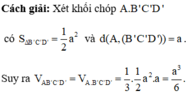
Cho hình hộp ABCD.A'B'C'D'. Tính tỉ số thể tích khối hộp đó và thể tích của khối tứ diện ACB'D' ?
Gọi S là diện tích đáy ABCD và h là chiều cao của khối hộp. Chia khối hộp thành khối tứ diện ACB’D’ và bốn khối chóp A.A’B’D’, C.C’B’D’, B’.BAC và D’. DAC. Ta thấy bốn khối chóp sau đều có diện tích đáy bằng và chiều cao bằng h, nên tổng các thể tích của chúng bằng
.
Từ đó suy ra thể tích của khối tứ diện
ACB’D’=. Do đó tỉ số của thể tích khối hộp đó và thể tích của khối tứ diện ACB’D’ bằng 3.
Cho hình lập phương ABCD.A'B'C'D' có cạnh a. Gọi M là trung điểm A'B' là trung điểm. Tính thể tích của khối tứ diện ADMN
A. V = a 3 3
B. V = a 3 12
C. V = a 3 6
D. V = a 3 2
Đáp án C
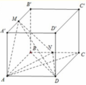
Ta có: S N A D = 1 2 d N ; A D . A D = 1 2 a 2
d M ; A B C D = A A ' = a
Do đó V M . A D N = 1 3 . A A ' . S N A D = a 3 6 .
Cho khối hộp ABCD.A'B'C'D có thể tích bằng 9. Tính thể tích khối tứ diện ACB'D'.
A. 3
B. 9 2
C. 6
D. 27 4