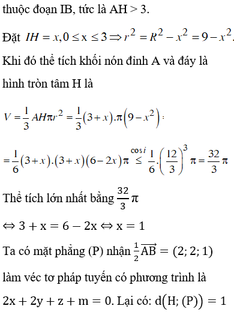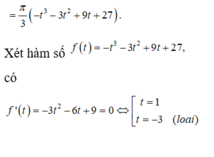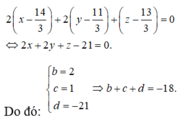Cho mặt cầu (S) có đường kính là AB biết rằng A(6; 2; -5), B(-4; 0; 7) Lập phương trình của mặt phẳng (α) tiếp xúc với mặt cầu (S) tại điểm A

Những câu hỏi liên quan
Cho mặt cầu (S) có đường kính là AB biết rằng A(6; 2; -5), B(-4; 0; 7) Lập phương trình của mặt cầu (S).
Cho mặt cầu (S) có đường kính là AB biết rằng A(6; 2; -5), B(-4; 0; 7) Tìm tọa độ tâm I và bán kính r của mặt cầu (S).
Tâm của mặt cầu (S) là trung điểm I (1; 1; 1) của đoạn thẳng AB và bán kính của mặt cầu (S) là R = IA = √62
Đúng 0
Bình luận (0)
Cho mặt cầu (S) có đường kính là AB, biết rằng A(6;2;-5), B(-4;0;7). Phương trình mặt phẳng (P) tiếp xúc mặt cầu (S) tại điểm A là A.
5
x
+
y
-
6
z
+
62
0
B.
5
x
+
y
-
6
z
-
62
0
C.
5
x
-
y...
Đọc tiếp
Cho mặt cầu (S) có đường kính là AB, biết rằng A(6;2;-5), B(-4;0;7). Phương trình mặt phẳng (P) tiếp xúc mặt cầu (S) tại điểm A là
A. 5 x + y - 6 z + 62 = 0
B. 5 x + y - 6 z - 62 = 0
C. 5 x - y - 6 z - 62 = 0
D. 5 x + y + 6 z - 62 = 0
Cho mặt cầu (S) có đường kính AB, biết rằng A(6;2;-5), B(-4;0;7). Tìm tọa độ tâm I và bán kính r của mặt cầu (S) A.
I
1
;
1
;
1
,
r
2
62
B.
I
-
1
;
-
1
;
-...
Đọc tiếp
Cho mặt cầu (S) có đường kính AB, biết rằng A(6;2;-5), B(-4;0;7). Tìm tọa độ tâm I và bán kính r của mặt cầu (S)
A. I 1 ; 1 ; 1 , r = 2 62
B. I - 1 ; - 1 ; - 1 , r = 248
C. I 1 ; 1 ; 1 , r = 62
D. I 1 ; 1 ; 1 , r = 62
Cho ba điểm A, B, C cùng thuộc một mặt cầu và biết rằng
∠
ACB 90
°
Khẳng định nào sau đây là đúng?A. AB luôn là đường kính của mặt cầu đã cho.B. Luôn luôn có một đường tròn thuộc mặt cầu ngoại tiếp tam giác ABC.C. Tam giác ABC vuông cân tại C.D. AB là đường kính của một đường tròn lớn trên mặt cầu đã cho.
Đọc tiếp
Cho ba điểm A, B, C cùng thuộc một mặt cầu và biết rằng ∠ ACB = 90 °
Khẳng định nào sau đây là đúng?
A. AB luôn là đường kính của mặt cầu đã cho.
B. Luôn luôn có một đường tròn thuộc mặt cầu ngoại tiếp tam giác ABC.
C. Tam giác ABC vuông cân tại C.
D. AB là đường kính của một đường tròn lớn trên mặt cầu đã cho.
Chọn B.
Mặt phẳng (ABC) cắt mặt cầu theo đường tròn ngoại tiếp tam giác ABC.
Đúng 0
Bình luận (0)
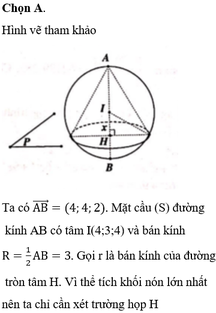
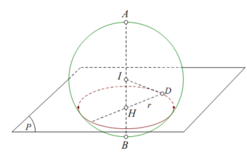
Trong không gian tọa độ Oxyz, cho hai điểm A(2;1;3), B(6;5;5). Gọi (S) là mặt cầu có đường kính AB. Mặt phẳng (P) vuông góc với đoạn AB tại H sao cho khối nón đỉnh A và đáy là hình tròn tâm H (giao của mặt cầu (S) và mặt phẳng (P) có thể tích lớn nhất, biết rằng (P)+2x+by+cz+d0 với b,c,d∈Z. Tính Sb+c+d. A. S -18. B. S -11 C. S -24 D. S -14
Đọc tiếp
Trong không gian tọa độ Oxyz, cho hai điểm A(2;1;3), B(6;5;5). Gọi (S) là mặt cầu có đường kính AB. Mặt phẳng (P) vuông góc với đoạn AB tại H sao cho khối nón đỉnh A và đáy là hình tròn tâm H (giao của mặt cầu (S) và mặt phẳng (P) có thể tích lớn nhất, biết rằng (P)+2x+by+cz+d=0 với b,c,d∈Z. Tính S=b+c+d.
A. S = -18.
B. S = -11
C. S = -24
D. S = -14
Trong hệ tọa độ Oxyz, cho mặt cầu (S) có đường kính là AB biết rằng \(A\left(6;2;-5\right);B\left(-4;0;7\right)\) :
a) Tìm tọa độ tâm I và tính bán kính r của mặt cầu (S)
b) Lập phương trình của mặt cầu (S)
c) Lập phương trình của mặt phẳng \(\left(\alpha\right)\) tiếp xúc với mặt cầu (S) tại điểm A
Trong không gian với hệ trục tọa độ Oxyz cho hai điểm A (2;1;3), B (6;5;5). Gọi (S) là mặt cầu đường kính AB Mặt phẳng (P) vuông góc với AB tại H sao cho khối nón đỉnh A và đáy là hình tròn tâm H (giao của mặt cầu (S) và mặt phẳng (P)) có thể tích lớn nhất, biết rằng (P): 2x + by + cz + d 0 với b,c,d
∈
Z. Tính S b + c + d . A. S 18 B. S -18 C. S -12 D. S 24
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho hai điểm A (2;1;3), B (6;5;5). Gọi (S) là mặt cầu đường kính AB Mặt phẳng (P) vuông góc với AB tại H sao cho khối nón đỉnh A và đáy là hình tròn tâm H (giao của mặt cầu (S) và mặt phẳng (P)) có thể tích lớn nhất, biết rằng (P): 2x + by + cz + d = 0 với b,c,d ∈ Z. Tính S = b + c + d .
A. S = 18
B. S = -18
C. S = -12
D. S = 24
Cho mặt cầu (S) có bán kính bằng 3 (m), đường kính AB. Qua A và B dựng các tia
A
t
1
,
B
t
2
tiếp xúc với mặt cầu và vuông góc với nhau. M và N là hai điểm lần lượt di chuyển trên
A
t
1
,
B
t
2
sao cho MN cũng tiếp xúc với (S). Biết rằng khối tứ diện ABMN có thể tích
V
m...
Đọc tiếp
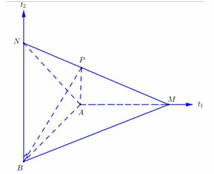
Cho mặt cầu (S) có bán kính bằng 3 (m), đường kính AB. Qua A và B dựng các tia A t 1 , B t 2 tiếp xúc với mặt cầu và vuông góc với nhau. M và N là hai điểm lần lượt di chuyển trên A t 1 , B t 2 sao cho MN cũng tiếp xúc với (S). Biết rằng khối tứ diện ABMN có thể tích V m 3 không đổi. V thuộc khoảng nào sau đây?
A. (17;21)
B. (15;17)
C. (25;28)
D. (23;25)