Cho hình chóp tứ giác đều có cạnh đáy bằng a và chiều cao bằng a 3 2 . Tính số đo góc giữa mặt bên và mặt đáy.
A. 60 0
B. 30 0
C. 75 0
D. 45 0
Cho hình chóp tứ giác đều có cạnh đáy bằng a và chiều cao bằng a 3 2 . Tính số đo của góc giữa mặt bên và mặt đáy
A. 45 °
B. 75 °
C. 30 °
D. 60 °
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, đường cao của hình chóp bằng a 3 2 . Tính số đo góc giữa mặt bên và đáy
A. 30 o
B. 45 o
C. 60 o
D. 90 o
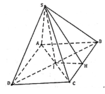
Ta có:
S I = a 3 2 ; I H = a 2 ⇒ tan I H S ^ = S I H I = 3 ⇒ S B C ; A B C D ^ = I H S ^ = 60 o
Đáp án C
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, chiều cao của chóp bằng a 3 2 . Góc giữa mặt bên và mặt đáy bằng
A. 60 °
B. 75 °
C. 30 °
D. 45 °
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, chiều cao của chóp bằng a 3 2 . Góc giữa mặt bên và mặt đáy bằng
![]()
![]()
![]()
![]()
Cho hình chóp tứ giác đều có cạnh đáy bằng a và độ dài đường cao bằng 14 a 2 . Tính tang của góc giữa cạnh bên và mặt đáy
A. 7
B. 14 2
C. 14
D. 7 2
Cho hình chóp tứ giác đều có cạnh đáy bằng a và độ dài đường cao bằng a 14 2 .Tính tang của góc giữa cạnh bên và mặt đáy
A. 7
B. 14 2
C. 14
D. 7 2
Chọn A
Phương pháp:
Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó.
Cách giải

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc giữa cạnh bên với mặt phẳng đáy bằng ∝
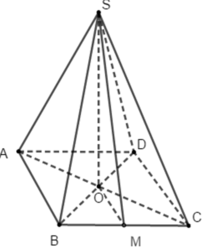
Tan của góc giữa mặt bên và mặt đáy bằng:
A. tan α
B. c o t α
C. 2 tan α
D. 2 2 tan α
Chân đường cao hình chóp đều S.ABCD trùng với tâm O của đáy ABCD. AO là hình chiếu của SA lên (ABCD)
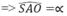
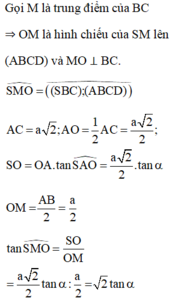
Đáp án C
Cho hình chóp tứ giác đều S.ABCD các cạnh đáy bằng a, góc giữa cạnh bên SA và mặt đáy bằng 30 o . Tính diện tích xung quanh S x q của hình trụ có một đường tròn đáy là đường tròn nội tiếp hình vuông ABCD và chiều cao bằng chiều cao của hình chóp S.ABCD
A. S x q = π a 2 6 12
B. S x q = π a 2 3 12
C. S x q = π a 2 3 6
D. S x q = π a 2 6 6
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và đường cao SH bằng cạnh đáy. Tính số đo góc hợp bởi cạnh bên và mặt đáy.
\(+\) vì \(SH\perp\left(ABC\right)\) và \(AN\subset\left(ABC\right)\Rightarrow SH\perp AN\) hay \(\Rightarrow SH\perp AH\)
\(\Rightarrow\) \(AH\) là hình chiếu vuông góc của \(SA\) lên \(\left(ABC\right)\) \(\Rightarrow\left(SA,\left(ABC\right)\right)=\left(SA,AH\right)=\widehat{SAH}\)
\(+\) gọi \(M,N\) lần lượt là t/điểm \(AC,BC\)
vì \(\Delta ABC\) là tam giác đều cạnh \(a\) nên dễ tính được : \(AN=\dfrac{a\sqrt{3}}{2}\)
từ giả thiết , suy ra \(H\) là trọng tâm \(\Delta ABC\)
\(\Rightarrow\) \(AH=\dfrac{2}{3}AN=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\)
\(+\) áp dụng hệ thức lược trong tam giác \(SHA\) vuông tại \(H\) , có :
\(tan\widehat{SAH}\) \(=\dfrac{SH}{AH}=\dfrac{a}{\dfrac{a\sqrt{3}}{3}}=\sqrt{3}\Rightarrow\widehat{SAH}\) \(=60^o\)